Q1 A long uniform rope of mass $M$ is suspended from a rigid end, calculate longitudinal strain due to its own wt. Diameter and young’s modulus of rope are $D$ and $Y$ respectively.
$\cfrac{2Mg}{\pi D^2 Y}$
Q2 A particle oscillating simple harmonically with an amplitude of $1.5 \ cm$, has a maximum energy of $0.25 \ \mu J$. At what displacement from the equilibrium position will the particle be acted upon by a force of $2.5 \times 10^{-5} \ N$?
$1.125 \ cm$
Q3 A small bob of mass $50 \ g$ oscillates as a simple pendulum, with an amplitude of $5 \ cm$ and period of $2 \ s$. Find the velocity of the bob and the tension in the supporting thread, when the velocity of the bob is maximum. [Take $g = 10 \ m/s^2$]
$0.157 \ m/s, \ 0.5 \ N$
Q4 A uniform rod of mass $m$ and length $l$ is free to rotate about a fixed horizontal axis through its end and perpendicular to its length. Find the period of small oscillations of the rod.
$2 \pi \sqrt{\cfrac{2l}{3g}}$
Q5 Find the distance from the top end of a uniform bar of length $24 \ cm$ which is to be mounted on a wall about an axis perpendicular to its length, so that its time period of oscillation will be minimum.
$12 – 2\sqrt{12} = 5.08 \ cm$
Q6 Two light wires made up of same material (Young Modulus, $Y$) have length $L$ each and radii $R$ and $2R$ respectively; they are joined together and suspended from a rigid support. Now a weight $W$ attached to the free end of joint wire as shown in figure. Find the elastic potential energy stored in the system due to extension of wire.
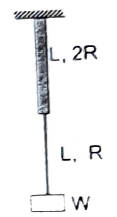
$\cfrac{5W^2 L}{8 \pi R^2 Y}$
Q7 A particle of mass $’m’$ is located in a unidimensional potential field where potential energy of the particle depends on coordinate $x$ as $u(x) = u_0 (1 – \cos cx)$ ; $u_0$ and $c$ are constants. Find the period of small oscillations that the particle performs about the equilibrium position.
$2\pi \sqrt{\cfrac{m}{u_0 c^2}}$
Q8 If a particle of mass $m$ moves in a potential energy field $U = u_0 – ax + bx^2$ where $u_0, \ a$ and $b$ are positive constant. Calculate the force constant, frequency of the particle and point of equilibrium.
$K = 2b, \ f = \cfrac{1}{2 \pi}\sqrt{\cfrac{2b}{m}}, \ x = \cfrac{a}{2b}$
Q9 A uniform heavy rod of weight $W$, cross sectional area $A$ and length $L$ is hanging from a fixed support. Young’s modules of the material of the rod is $Y$; find the elongation of the rod due to its own weight and potential energy stored, Neglect the lateral contraction.
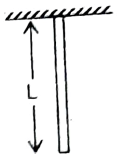
$\cfrac{WL}{2 A Y}$, potential energy $ = \cfrac{1}{6} \cfrac{W^2 l}{AY}$
Q10 Two particles execute SHM parallel to $x$-axis about the origin with the same amplitude and frequency. At a certain instance they are found at distance $A/3$ from the origin on opposite side but their velocities are found to be in opposite direction. Find the phase difference between the two.
$\pi$
Q11 A container contains liquid of variable density which varies as $d = d_0 \left(4 – \cfrac{3y}{h_0}\right) \ kg /m^3$, where $h_0$ and $d_0$ are constants and $y$ is measured from the bottom of container as shown in the figure. A solid block whose density is $(5/2) d_0$ and mass $m$ is released from the bottom of the container. Prove that the block will execute SHM and calculate its time period.
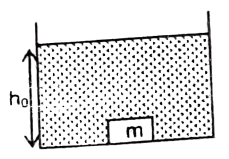
$T = 2 \pi \sqrt{\cfrac{5h_0}{6g}}$
Q12 A ring of mass $m$ and radius $’a’$ is connected to an inextensible string which passes over a frictionless pulley. The other end of the string is connected to upper end of a massless spring of spring constant $k$. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of the ring is in equilibrium position, then find time period of small oscillations of the ring.
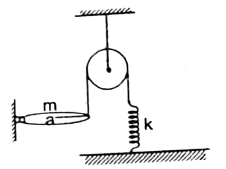
$2 \pi \sqrt{\cfrac{3m}{8k}}$
Q13 A spring mass system is hanging from the ceiling of an elevator in equilibrium. The elevator suddenly starts accelerating upwards with acceleration a find
(a) the frequency and
(b) the amplitude of the resulting SHM.
(a) $2 \pi \sqrt{\cfrac{m}{k}}$
(b) $\cfrac{ma}{k}$
Q14 Three thin rods of mass $M$ and length $l$ make three sides of a triangle. When suspended from one of the vertices of the triangle find the time period of oscillation of the pendulum thus formed in oscillating in a vertical plane.
$2 \pi \sqrt{\cfrac{\sqrt{3}}{2}\cfrac{l}{g}}$
Q15 In the shown figure, mass $m$ rests on smooth horizontal surface, connected with an ideal spring. If the mass $m$ is displaced to the point $A$ and released from rest, it reaches the point $O$ in time $t_0$. Now the block is displaced to the point $B$ and released from rest. How much time it will take in traveling from point $A$ to point $O$.
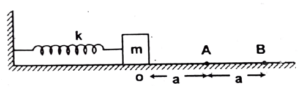
$\cfrac{t_0}{3}$
Q16 A block of mass $’m’$ is attached to a spring and is placed on a platform as shown in the figure, and the spring at this stage remains in a relaxed stage. When supporting platform is suddenly removed the mass begins to oscillate and moves down to a lowest position of $5 \ cm$ from its initial position. Then calculate the time taken by block to reach a height of $3 \ cm$ from its lowest position?
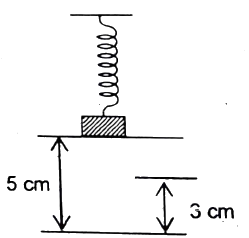
$\cfrac{\pi}{40} + \cfrac{1}{20} \sin^{-1} (1/5)$
Q17 There is a rectangular frame on which two semicircular rings each having mass $m$ are connected such that its ends can slip on the sides of the frame. Initially both the rings are connected by a unstretched spring of natural length $l_0$ and of spring constant $k$ are touching each other to form a circle. There is thin film (surface tension $T$) between the semi circular rings and frame as shown in figure.
(a) Find the elongation of spring in the equilibrium position of rings.
(b) Find the period of the subsequent SHM,
[Assume that spring is passing though center of the circle and whole system is placed on a smooth horizontal plane.]
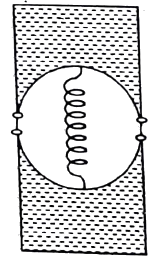
(a) $x_0 = \cfrac{2T l_0}{k}$,
(b) $T = 2 \pi \sqrt{\cfrac{m}{2k}}$
Q18 A block of mass $’m’$ connected by a spring is kept on a horizontal frictionless floor. When the spring is at its natural length $’l_0’$, the block is at a distance $’a’$ from the wall. Now, the block is moved by a distance of $’2a’$ away from the wall and released. If the collision between the block and wall is elastic, determine the time period of oscillation ?
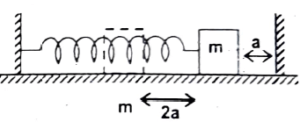
$T = \cfrac{2}{3} \left(2 \pi \sqrt{\cfrac{m}{k}}\right)$
Q19 A solid cylinder of mass $m$ and radius $R$ is kept in equilibrium on a horizontal rough surface. Three unstretched springs of spring constants $k, \ 2k, \ 3k$ are attached to cylinder as shown in the figure. Find the period of small oscillations. (Given that surface is rough enough to prevent slipping of cylinder.)
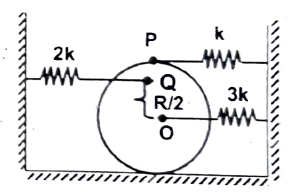
$T = 2 \pi \sqrt{\cfrac{3m}{23k}}$
Q20 A spherical ball of mass $m$ and radius $r$ rolls without slipping on a concave surface of large radius $R$. Find the time period of small oscillations about the lowest point.
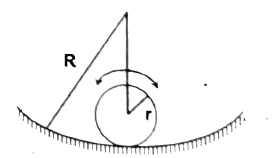
$2 \pi \sqrt{\cfrac{7(R- r)}{5g}}$
Q21 Three particles of the same mass $m$ are fixed to a uniform circular hoop of mass $m$ and radius $R$ at the corners of an equilateral triangle. The hoop is free to rotate in a vertical plane about the point on the circumference opposite to one of the masses. Find the equivalent length of a simple pendulum.
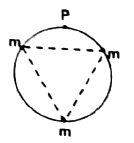
$2R$
Q22 An elastic string of natural length $2a$ can support a certain weight extending to a total length of $3a$. One end of the string is now attached to a point on a smooth horizontal table and the same weight is attached to the other end and can move on the table. Show that, if the weight is pulled to any distance and let go, the string slacks after a time $\cfrac{\pi}{2} \sqrt{\cfrac{a}{g}}$
Q23 A particle in S.H.M. crosses its equilibrium position at time $t =2 \ sec$. When the motion advances by one second more, its velocity is found to be $\pi/3 \ m/s$. If the frequency of the motion is $1/6 \ s^{-1}$, find the amplitude of the motion in meter.
$2$
Q24 A particle executes SHM along $x$-axis with a frequency $\left(\cfrac{25}{\pi}\right) \ Hz$. The mass of the particle is $0.20 \ kg$. At the position $x = 0.04 \ m$, the kinetic energy is $0.50 \ J$. The potential energy is zero at mean position. Find the amplitude of oscillations (in $cms$).
$6$
Q25 Force acting on a particle is $F = – 8x$ in SHM. The amplitude of oscillations is $2$(in $m$) and mass of the particle is $0.5 \ kg$. the total mechanical energy of the particle is $20 \ J$. Find the potential energy of the particle in mean position (in $J$)
$4$
Q26 A body of mass $10 \ kg$ is connected to a wire of length $0.3 \ m$ and of cross-sectional area $10^{-6} \ m^2$. Its breaking strength is $4.8 \times 10^7 \ N/m^2$. Find the maximum angular velocity with which it can be rotated in a horizontal circle (in $rad/sec$).
$4$