Q1 A fixed wedge $ABC$ is in the shape of an equilateral triangle of side $l$. Initially, a chain of length $2l$ and mass $m$ rests on the wedge as shown. The chain is slowly being pulled down by the application of a force $F$ as shown. Find the work done by gravity till the time, the chain leaves the wedge.
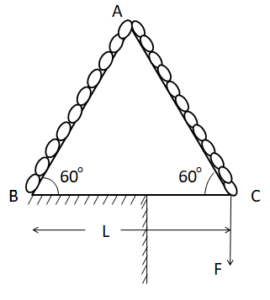
Correct answer is $\left(\cfrac{(\sqrt{3} + 4)mgl}{4}\right)$.
Q2 A mass $’m’$ moves with velocity $v = \sqrt{3} \ m/s$ and collides with another mass $2m$ initially at rest. After collision first mass move with velocity $\cfrac{v}{\sqrt{3}}$ in the direction perpendicular to initial direction of motion. Speed of second mass (in $m/s$) after collision is ……….
Correct answer is $1$.
Q3 There are four rods $A, \ B, \ C$ and $D$ of same length $l$ but different linear mass density, $d, \ 2d, \ 3d$ & $4d$ respectively. These are joined to form a square frame with sides $C$ & $D$ along $x$ & $y$ axis of coordinate axes respectively. Find coordinate of center of mass of structure.
Correct answer is $\left(\cfrac{4l}{10}, \ \cfrac{4l}{10}\right)$
Q4 A body of mass $M$ as shown in figure with a small disc of mass $m$ placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity $v$. To what height (relative to the initial level) will the disc rise after breaking off the body $M$ (assume that just after collision it moves vertically upward)? The friction is assumed to be absent.
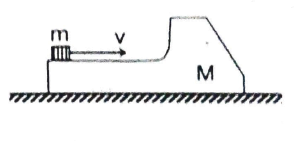
Correct answer is $H = Mv^2/2g(M + m)$.
Q5 There is a thin uniform disc of radius $R$ and mass per unit area $\sigma$, in which a hole of radius $R/2$ has been cut out as shown in the figure. Inside the hole a square plate of same mass per unit area $\sigma$ is inserted so that its corners touch the periphery of the hole. Find center of mass of the system.
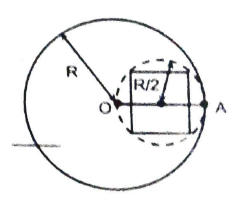
Correct answer is $\cfrac{R[2 – \pi]}{2[3 \pi + 2]}$.
Q6 A ball moving with velocity $\hat{i}$ collides with a stationary wall and returns with a velocity $\hat{j}/2$. The coefficient of restitution for this collision is $1/K$. Find the value of $K$.
Correct answer is $4$.
Q7 Two balls of masses $1 \ kg$ each are connected by an inextensible massless string. The system is resting on a smooth horizontal surface. An impulse of $10 \ Ns$ is applied to one of the balls at an angle $30^{\circ}$ with the line joining two balls in horizontal direction as shown in the figure. Assuming that the string remains taut after the impulse, the magnitude of impulse of tension is $\cfrac{K}{2} \sqrt{3} \ Ns$. Find the value of $K$.
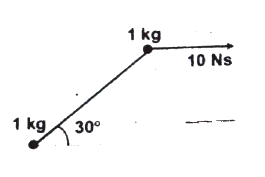
Correct answer is $5$.
Q8 A ball is moving with velocity $2 \ m/s$ towards a heavy wall moving towards the ball with speed $1 \ m/s$ as shown in figure. Assuming collision to be elastic, find the velocity(in $m/s$) of ball immediately after the collision.
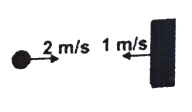
Correct answer is $4$.
Q9 Three balls $A, \ B$ and $C$ are placed on a smooth horizontal surface. Given that $m_A = m_C = 4m_B$. Ball $B$ collides with ball $C$ with an initial velocity $v$ as shown in figure. Find the total number of collisions between the balls. All collisions are elastic.

Correct answer is $2$.
Q10 A small particle travelling with a velocity $v$ collides elastically with a smooth spherical body of equal mass and of radius $r$ initially kept at rest. The center of this spherical body is located a distance $\rho(<r)$ away from the direction of motion of the particle. Find the final velocities of the two bodies.
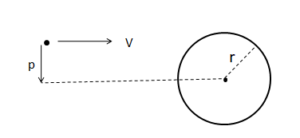
Correct answers are
velocity of sphere $ = \cfrac{v\sqrt{r^2 – \rho^2}}{r}$ along common normal.
velocity of particle $ = \cfrac{v \rho}{r}$ along common tangent.
Q11 A railroad car is moving along a straight frictionless track. In each of the following cases, the car initially has a total mass (car and contents) of $200 \ kg$ and is travelling with a velocity of $4 \ m/s$. Find the final velocity of the car in each of the three cases.
(a) A $20 \ kg$ mass is thrown sideways out of the car with a velocity of $2 \ m/s$ relative to the car.
(b) A $20 \ kg$ mass is thrown backward out of the car with a velocity of $4 \ m/s$ relative to the car.
(c) A $20 \ kg$ mass is thrown into the car with a velocity of $6 \ m/s$ relative to the ground and opposite in direction to the velocity of the car.
Correct answers are
(a) $4 / m\s$ in the same direction
(b) $4.4 / m\s$ in the same direction
(c) $3.1 / m\s$ in the same direction
Q12 A cubical block of mass $m$ is released from rest at a height $h$ on a frictionless surface of a movable wedge of mass $M$, which is, in turn is placed on a horizontal frictionless surface as shown in the figure. Find the velocity of the triangular block when the smaller block reaches the bottom.
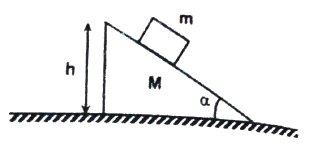
Correct answer is $\left[\cfrac{2m^2 gh \cos^2 \alpha}{(M + m)(M + m \sin^2 \alpha)}\right]^{1\2}$
Q13 A projectile of mass $m$ is fired with a velocity $v_0$ at an angle $\theta$ with the horizontal. At the highest position in its fight, it explodes into two fragments of masses $m_1 = \cfrac{m}{3}$ and $m_2 = \cfrac{2m}{3}$.
The fragment of mass $m_1$ falls vertically with zero initial speed.
(a) Find the initial velocity of the fragment $m_2$.
(b) Find the distance $d$ at which the fragment $m_2$ will land with respect to $m_1$.
Correct answers are
(a) $\cfrac{3}{2} v_0 \cos \theta$.
(b) $\cfrac{3v_0^2 \sin \theta \cos \theta}{2g}$
Q14 Block $A$ in the figure has a mass of $1 \ kg$ and block $B$ has a mass of $2 \ kg$. The blocks are forced together compressing a massless spring between them and the system is released from rest on a level frictionless surface. The spring is not fastened to either of the blocks, when spring regains its natural length, block $B$ acquired a speed of $0.5 \ m/s$. How much potential energy was stored in the compressed spring ?
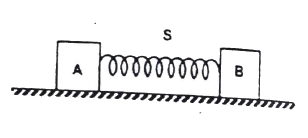
Correct answer is $0.75 \ J$
Q15 A particle of mass $m$ moving with a speed $u$ strikes a smooth horizontal surface at an angle $\alpha$. The particle rebounds at angle $\beta$ with a speed $v$. Determine the expression for $v$ and $\beta$ if the coefficient of restitution is $e$.
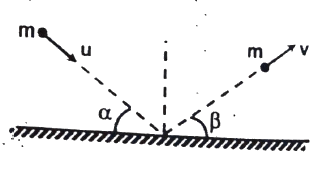
Correct answers are
$v = u \sqrt{e^2 \sin^2 \alpha + \cos^2 \alpha}, \ \tan \beta = e \tan \alpha$
Q16 A bulled of mass $20 \ g$ travelling horizontally with a speed of $500 \ m/s$ passes through a wooden block of mass $10.0 \ kg$ initially at rest to a level surface. The bullet emerges with a speed of $100 \ m/s$ and the block slides $20 \ cm$ on the surface before coming to rest. Find the friction coefficient between the block and the surface in the figure. ($g = 10 \ m/s^2$)
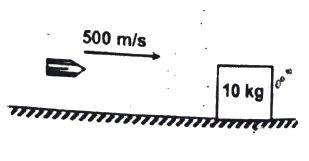
Correct answer is $0.16$.
Q17 A spring of spring constant $k$ connects two bocks of masses $m_1$ and $m_2$ as shown in the figure. The block of mass $m_2$ is given a sharp impulse so that it acquires a velocity $V_0$ towards right . Find
(a) the velocity of the center of mass; and
(b) the maximum elongation of the spring.
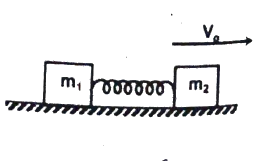
Correct answers are
(a) $\cfrac{m_2V_0}{m_1 + m_2}$
(b) $V_0\sqrt{\cfrac{m_1 m_2}{(m_1 + m_2)k}}$
Q18 Two beads of masses $m_1$ and $m_2$ are threaded on a smooth circular wire of radius $’a’$ fixed in a vertical pane. $B$ is stationary at the lowest point when $A$ is gently dislodged from rest at the highest point. $A$ collides with $B$ at the lowest point. The impulse given to $B$ due to collision is just great enough to carry it to the level of the center of the circle while $A$ is immediately brought to rest by the impact. Find $m_1 : m_2$.
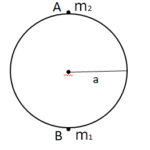
Correct answer is to be updated.
Q19 Three identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. At the moment $t = 0$, ball $B$ is imparted a velocity. Calculate the velocity of $A$ when it collides with ball $C$.
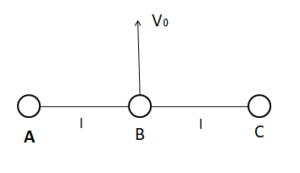
Correct answer is $\cfrac{2v_0}{3}$.
Q20 In the figure shown, a ball of mass $m$ collides perpendicularly on a smooth stationary wedge of mass $M$. kept on a smooth horizontal plane. If the coefficient of restitution of collision is $e$, then determine the velocity of the wedge after collision.
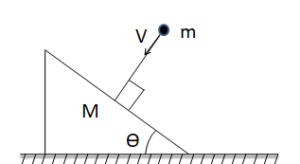
Correct answer is $\cfrac{(1 + e) m v_0 \sin \theta}{M + m \sin^2 \theta}$.
Q21 A uniform steel rod of $1 \ m$ in length is bent in a $90^{\circ}$ angle at its mid point. Determine the position of its center of mass from the corner at bent.
Correct answer is $\cfrac{1}{4\sqrt{2}} \ m$ from the corner along $45^{\circ}$ bisector line and inside the right angle.
Q22 A $1000 \ kg$ automobile is moving along a straight highway at $10 \ m/s$. Another car with mass $2000 \ kg$ is moving at speed $20 \ m/s$ at a distance of $30 \ m$ ahead of the first car.
(a) Find the total momentum from the above data.
(b) Find the velocity of the center of mass.
(c) Find the total momentum, using the velocity of the center of mass. Compare your result with that of part (a).
Correct answer is
(a) $50000 \ kg \ m/s$
(b) $\cfrac{50}{3} \ m/s$
(c) $50000 \ kg \ m/s$
Q23 Two balls of mass $m$ each moving in opposite directions with equal speed $v$ collide head on and elastically with each other. Find the final speeds of the balls after collision.
Correct answer is Both balls will have speed equal to $v$.
Q24 A $10 \ gm$ bullet is shot from a $5 \ kg$ gun with a speed of $400 \ ms^{-1}$. What is the speed of recoil of the gun ?
Correct answer is $0.8 \ ms^{-1}$
Q25 A body of mass $m$ is moving with speed $v$ makes an elastic one dimensional collision with a stationary body of same mass. They are in contact for very small time interval $\Delta{t}$. The contact force between them varies as shown in graph. Find the magnitude of $F_{\text{max}}$.
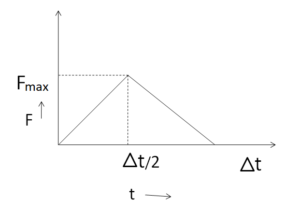
Correct answer is $\cfrac{2mv}{\Delta{t}}$.
Q26 A shell of mass $5 \ kg$ moving with a speed of $20 \ m/s$ explodes into two particles of $3 \ kg$ and $2 \ kg$. If the $3 \ kg$ particle just comes to rest after the explosion, find the speed of the $2 \ kg$ particle.
Correct answer is $50 \ m/s$.
Q27 A ball is dropped from a height $100 \ m$ on the ground. If the coefficient of restitution is $0.2$, what is the height to which the ball will go up after it rebounds for the second time.
Correct answer is $16 \ cm$.
Q28 A disc of radius $R$ is placed on a square plate of edge $4R$ made up of the same sheet with their planes parallel such that any two adjacent sides of square touch the disc. Find the distance of the center of mass of the system from the center of square plate.
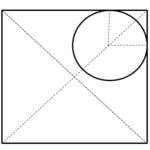
Correct answer is $\cfrac{\sqrt{2} \pi R}{16 + \pi}$.
Q29 An acrobat of mass $m$ clings to a rope ladder hanging below a balloon of mass $M$. The balloon is stationary with respect to ground.
(a) If the acrobat begins to climb the ladder at a speed $v$ (with respect to the ladder), in what direction and with what speed (with respect to the Earth) will the balloon move?
(b) If the acrobat stops climbing, what will be the velocity of the balloon?
Correct answers are
(a) down, $\cfrac{mv}{M + m}$.
(b) balloon-again becomes stationary.
Q30 A pulley fixed to a rigid support carries a rope whose one end is tied to a ladder with a man and the other end to the counterweight of mass $M$. The man of mass $m$ climbs up a distance $h$ with respect to the ladder and then stops. If the mass of the rope and the friction in the pulley axle are negligible, find the displacement of the center of mass of this system.
Correct answer is $\cfrac{mh}{2M}$.




