Center of Mass of Two or More Particle Systems

Here is the center of mass of two (or more) particle systems

Two Particle System

Moment of inertia of two particle system
Moment of inertia of two particle system

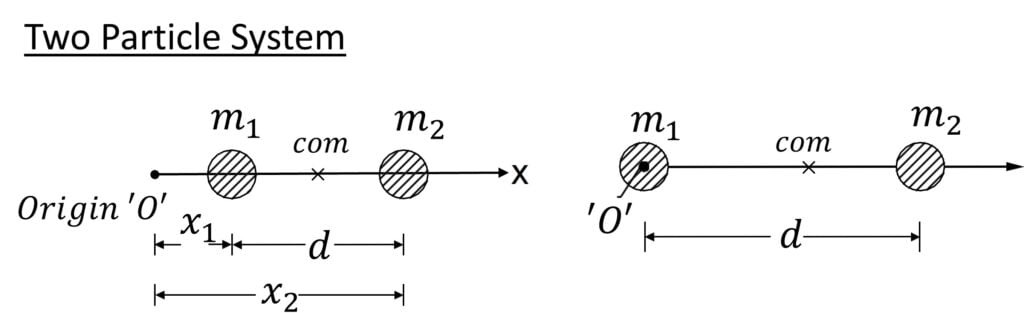
For the scenario on the left:
$x_{CM} = \cfrac{m_1 x_1 + m_2 x_2}{m_1 + m_2}$ $=x_1 + \cfrac{m_2 d}{m_1 + m_2}$

For the scenario on the right
$x_{CM} = \cfrac{m_2 d}{m_1 + m_2}$

Note:
(i) If $m_1 > m_2$, $x_{CM} < \cfrac{d}{2}$ (i.e. $x_{CM}$ is located closer to $m_1$)
(ii) If $m_1 < m_2$, $x_{CM} > \cfrac{d}{2}$ (i.e. $x_{CM}$ is located closer to $m_2$) 

Multiple Particle System

Moment of inertia of multi particle system
Moment of inertia of multi particle system

For a system comprising of two or more simple rigid bodies (with the known center of masses), let’s determine the center of mass of the system. OR for a simple rigid body, such as a disc, with a cut out of a standard shape (for example circle or square, etc.), let’s determine its center of mass

$\color{blue}{\text{Solution Steps}}$
A : $x_{cm} =$ $\cfrac{\sum m_i x_i}{\sum m_i}$
$=\cfrac{\sum_A m_ix_i + \sum_B m_ix_i}{m_A+m_B}$
$= \cfrac{m_Ax_{cm,A} + \sum_B m_B x_{cm,B}}{m_A+m_B}$
$y_{cm} = \cfrac{\sum m_i y_i}{\sum m_i}$
$=\cfrac{\sum_A m_iy_i + \sum_B m_iy_i}{m_A+m_B}$
$= \cfrac{m_Ay_{cm,A} + \sum_B m_B y_{cm,B}}{m_A+m_B}$

B) : $\tan \theta = \cfrac{x_{cm}}{L-y_{cm}}$
$x_{cm} = \cfrac{m.0+m.L/2}{2m}, \quad y_{cm}$
$= \cfrac{m.L/2 + m.0}{2m}$
$x_{cm} = y_{cm} = \cfrac{L}{4}$
$\theta = \tan^{-1} \cfrac{1}{3}$

C) : $(m_1 + m_2)x_{cm}$ $= m_1x_{cm,1} + m_2 x_{cm,2}$
$x_{cm} = 0$
$x_{cm,2} = – \cfrac{m_1x_{cm,1}}{m_2}$

To continue to explore center of mass of other commonly encountered shapes, click here…

JEE Physics Online Classes