Fictitious Forces | Centrifugal Force
A fictitious force is a force that ‘appears’ to act on a mass when it’s motion is described using an accelerating frame of reference. Note that the observer on the ground or non accelerating or inertial frame of reference would deny existence of these forces and he/she will claim that the observer in the accelerating frame of reference has been deceived in believing that such a force exists. For example, in case of an airplane accelerating down the runway, an observer inside the airplane would claim that there is an invisible force is acting on the passengers and pushing them back into their seats
Now, centrifugal force is one such fictitious force that appears to act on objects when viewed by an observer in a rotating (accelerating) frame of reference.
So, let’s take a look at some of the examples of such fictitious or imaginary forces, and then we will recap the differences between centripetal and centrifugal forces.
Afterwards you will get to practice 10 questions, where in you can solve for the unknown in inertial frame of reference (no centrifugal forces) or we can solve for them in non-inertial or accelerating frame of reference (wherein we will have centrifugal forces)
Centrifugal force examples
Vehicle driving around a curve: When going around a curve the passengers inside the vehicle, say car, experience a fictitious radially outward force which in reality is their upper body trying to follow the straight line path but lower body due to radially inwards frictional force between car seat and the person is trying to move around the circular path
Stone on a string: When swinging a stone on a string in a circular path, a tension force develops in the string as if someone is pulling the stone radially outwards while in reality moving in a circle means that the particle is under centripetal acceleration ($= ]cfrac{v^2}{r}$) and so there must be a centripetal force to provide that acceleration else the stone will tend to fly off in a straight line path
Weight of an object at the poles vs it’s weight at the poles: Weight $N$ reported on the equator $=mg – m \omega^2 r$, where $r$ is the radius of the earth while at poles it will be $= mg$. This is because part of the gravitational force $mg$ is consumed in turning the object along with the earth as it rotates with angular velocity $\omega$
Difference between centripetal and centrifugal Force
Centripetal Forces:
1. Real forces (for example tension in string or normal force or electrostatic force) pointed radially inwards i.e. towards the center
2. These forces are what turns the direction of velocity vector of the particle as it moves around a circular path
3. Observer in inertial frame of reference will write the newton’s 2nd law as
$F_{centripetal} = \cfrac{mv^2}{r}$
Centrifugal Forces:
1. Fictitious force as reported by observer in the accelerating frame of reference and they will appear to be pointed radially outwards
2. For the observer in the rotating frame of reference, the particle appears stationary and since it is stationary he/she concludes that there must a fictitious force countering centripetal forces
3. Observer in non-inertial or rotating frame of reference will write the newton’s 2nd law as
$F_{net, \ radial} = 0$
or
$F_{centripetal} + F_{centrifugal} = 0$
where
$F_{centrifugal} =$ $\cfrac{mv^2}{r}$.
Practice Problems (involving use of fictitious force)
Now let’s solve the following problems in inertial as well as in non inertial frames of reference for better understanding.
Once again note that in inertial frame of reference we will use $F_{net, \ external} = m a_{centripetal}$ while in non inertial frame of reference, i.e. in the frame of reference of accelerating platform we will introduce centrifugal force $= -ma_{centripetal}$ and then solve the problem at hand
Now, the following practice problems have been divided into 3 scenarios
1) Linearly accelerating frame of reference: The platform is accelerating along a given direction and the given particle is moving along a straight line with respect to this accelerating platform
2) Linear accelerating frame of reference: The platform is accelerating along a given direction and the given particle is moving along a circular path with respect to this accelerating platform
3) Rotating frame of reference : The platform is rotating about an axis and the given particle is either stationary or moving along a straight line with respect to this rotating platform.
Linearly accelerating platform | Translational motion of mass placed on the accelerating platform
Q1 A block of mass $m$ is placed on an inclined plane. With what acceleration $a$, towards right, should the system move on a horizontal surface so that $m$ does NOT slide on the surface of the inclined plane? Assume all surfaces to be smooth.
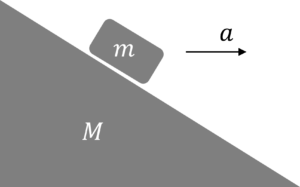
Answer
$a = g \tan \theta$
Q2 A pendulum of mass $m$ is hanging from the ceiling of a car having an acceleration $a$ with respect to the road in the direction shown. Find the angle $\theta$ made by the string with the vertical.

Answer
$\theta = \tan^{-1} (\cfrac{a}{g})$
Q3 A block of mass $m$ lies on the surface of lift. Find the normal contact force between the block and the floor of the lift when lift is moving downward with constant acceleration $a<g$.
Answer
$N=m(g-a)$
Q4 A wedge of mass $m_1$ and with angle $\alpha$ rests on a horizontal surface. A block of mass $m_2$ is placed on the wedge, which rests on the wedge. Assuming the friction to be negligible, find the acceleration of the wedge. Also find the acceleration of the block relative to the wedge

Answer
Acceleration of the wedge $= \cfrac{g \sin \alpha \cos \alpha}{\sin^2 \alpha + (m_1/m_2)}$
Acceleration of the block relative of the wedge $=\cfrac{1 + \cfrac{m_2}{m_1} g \sin \alpha }{(1 + \cfrac{m_2}{m_1} \sin^2 \alpha)}$
Q5. A circular disc with a groove along its diameter is placed horizontally. A block of mass $1 \ Kg$ is placed as shown. The coefficient of friction between the block and all surfaces of the groove in contact is $\mu = 2/5$. The disc has an acceleration of $25$ $m/s^2$. Find the acceleration of the block with respect to disc.
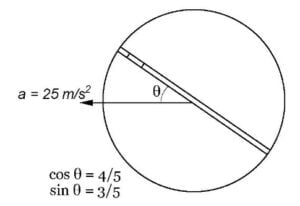
Answer
$10 \ m/s^2$
Linearly accelerating platform | Circular motion of mass placed on accelerating platform
Q6 A smooth sphere of radius $R$ is made to translate in a straight line with a constant acceleration $\alpha$. A particle kept on the top of the sphere is released from there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle $\theta$ it slides.
Answer
$[2R(\alpha \sin \theta + g – g \cos \theta)]^{1/2}$

Rotating frame of reference | Use of centrifugal force
Q7 In a children’s park a heavy road is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod. Let the mass of each kid be $15$ kg, the distance between the points of the rod where the two kids hold it be $3.0$ m and suppose that the rod rotates at the rate of $20$ revolutions per minute. FInd the force of friction exerted by the rod on one of the kids.
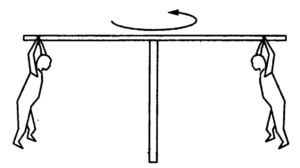
Answer
$10$ $\pi^2$
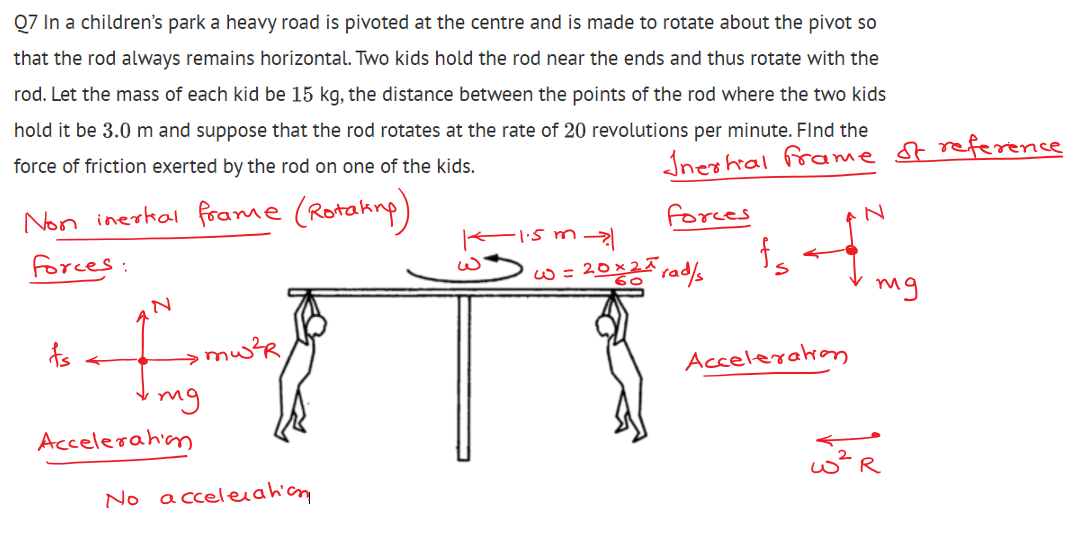
Q8 A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity $\omega$ in a circular path of radius $R$. A smooth groove $AB$ of length $L$ ($<<R$) is made on the surface of the table. The groove makes an angle $\theta$ with the radius $OA$ of the circle in which the cabin rotates. A small particle is kept at the point $A$ in the groove and is released to move along $AB$. Find the time taken by the particle to reach the point $B$.
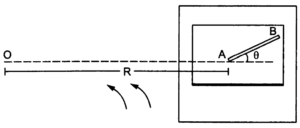
Answer
$\sqrt{\cfrac{2L}{\omega^2 R \cos \theta}}$
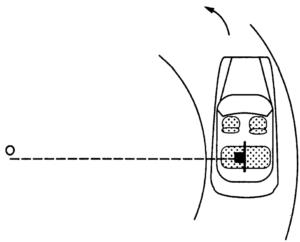
Q9 A car moving at a speed of $36$ km/hr is taking a turn on a circular road of radius $50$ m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road. A small block of mass $100$ g is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is $\mu = 0.58$.
If the plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
Answer
$30^\circ$
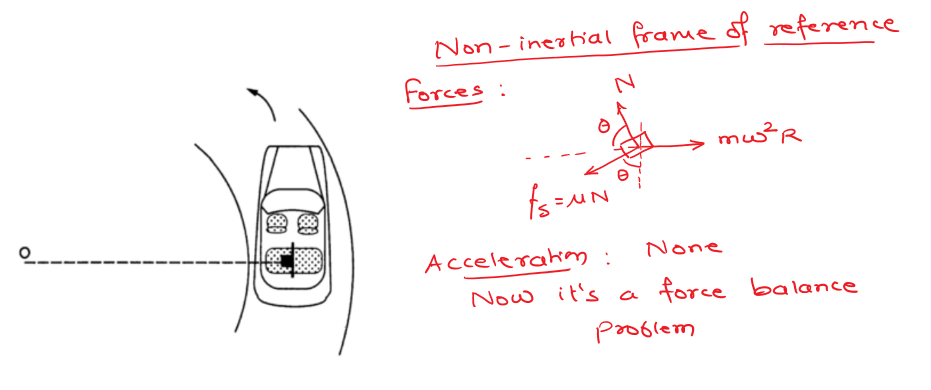
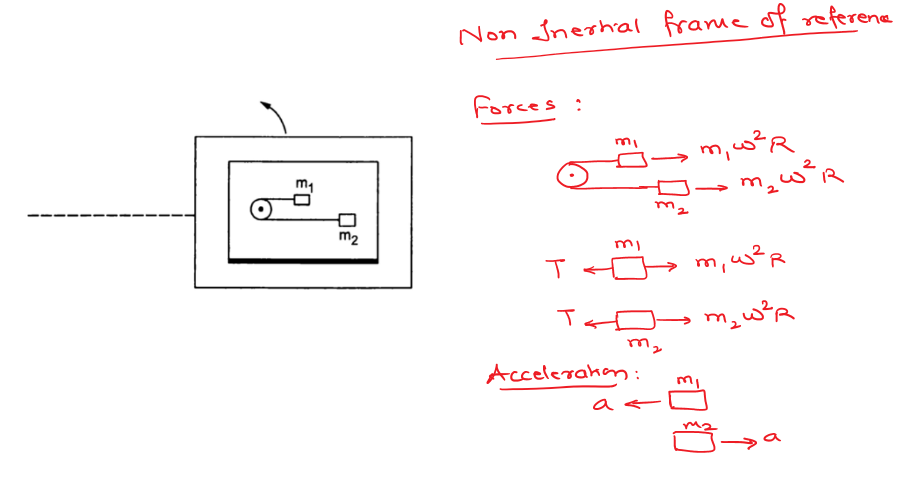
Q10 A table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius $R$. A smooth pulley of small radius is fastened to the table. Two masses $m$ and $2m$ placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the strings along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string
Answer
$\cfrac{\omega^2 R}{3}$, $\cfrac{4}{3} m\omega^2 R$
Hope that helped. Please feel free to comment if you have any questions or feedback.
Best Wishes