Here are the eight (8) JEE Main important questions from center of mass and linear momentum, which account for almost all the questions asked in JEE Main on this topic.
Listen through the audio podcasts and read through the solution steps on each of the question type and then corresponding practice JEE Main and NTA Abhyas questions at acejee.com > Dashboard > Center of Mass & Linear Momentum > Important Questions
$\color{blue}{\text{Important Question Type No. 3}}$
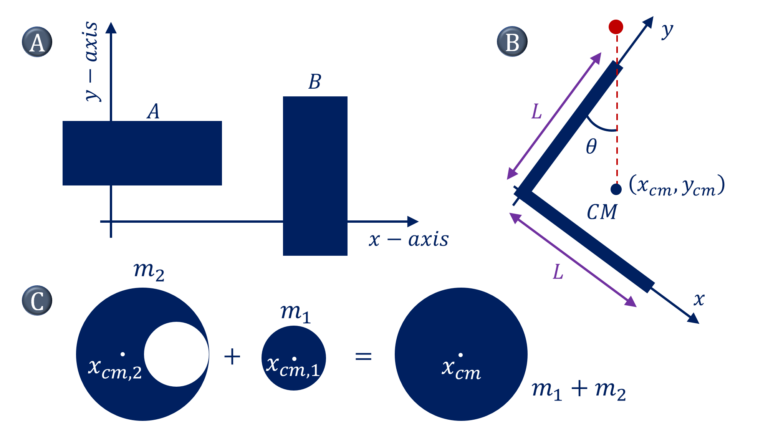
For a system comprising of two or more simple rigid bodies (with the known center of masses), determine the center of mass of the system. OR for a simple rigid body, such as a disc, with a cut out of a standard shape (for example circle or square, etc.), determine its center of mass
$\color{green}{\text{Solution Steps}}$
A) $x_{cm} =$ $\cfrac{\sum m_i x_i}{\sum m_i} =$ $\cfrac{\sum_A m_ix_i + \sum_B m_ix_i}{m_A+m_B}$
$= \cfrac{m_Ax_{cm,A} + \sum_B m_B x_{cm,B}}{m_A+m_B} $
$y_{cm} = $ $\cfrac{\sum m_i y_i}{\sum m_i} =$ $\cfrac{\sum_A m_iy_i + \sum_B m_iy_i}{m_A+m_B}$
$= \cfrac{m_Ay_{cm,A} + \sum_B m_B y_{cm,B}}{m_A+m_B}$
B) $\tan \theta = \cfrac{x_{cm}}{L-y_{cm}}$
$x_{cm} =$ $\cfrac{m.0+m.L/2}{2m}, \quad y_{cm} =$ $\cfrac{m.L/2 + m.0}{2m}$
$x_{cm} =$ $y_{cm} =$ $\cfrac{L}{4}$
$\theta =$ $\tan^{-1} \cfrac{1}{3}$
C) $(m_1 + m_2)x_{cm} =$ $m_1x_{cm,1} + m_2 x_{cm,2}$
$x_{cm} = 0$
$x_{cm,2} =$ $ – \cfrac{m_1x_{cm,1}}{m_2}$
$\color{blue}{\text{Important Question Type No. 6}}$
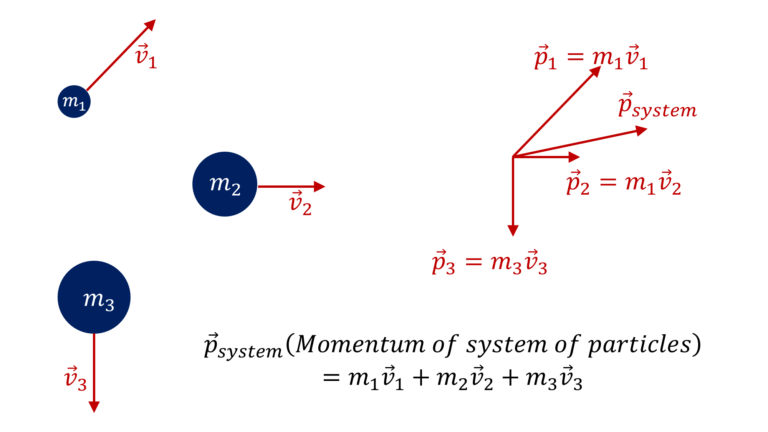
Given information (directly or indirectly) about the velocity of the particles of a system, determine the linear momentum of the system
$\color{green}{\text{Solution Steps}}$
$\bullet$ Linear momentum of a particle $\overrightarrow{p}$=m \overrightarrow{v}$
Note, the momentum of a particle moving with velocity, $\overrightarrow{v}$, relative to an observer moving at uniform velocity $\overrightarrow{u}$ is $=m (\overrightarrow{v} – \overrightarrow{u})$
$\bullet$ $\overrightarrow{P}_{system} = \sum m_i \overrightarrow{v}_i$
$\color{blue}{\text{Important Question Type No. 16}}$
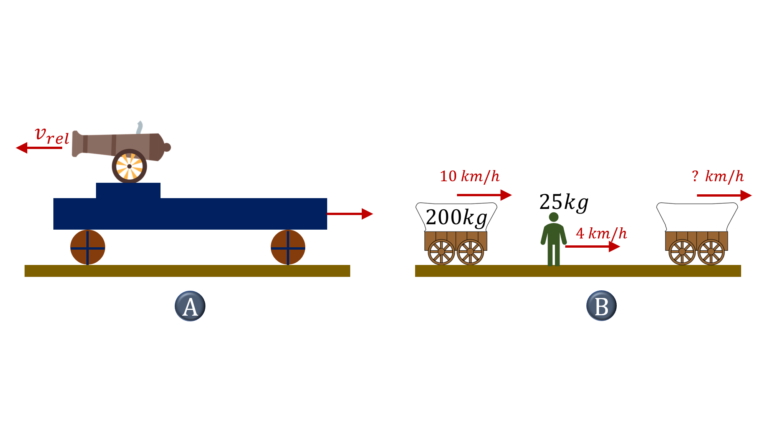
A) Given two or more masses moving away from each other, for example, a cannon on a train firing shells with some relative velocity or a mass exploding into two or more pieces, determine the velocity of the involved masses after the event.
B) Given two or more masses gently coming together along the horizontal direction with no net external forces in that direction, for example, a man walking along a buggy jumping on it, determine the velocity of the involved masses after the event.
C) Given that a system (such as a spaceship) is continuously losing or gaining mass at a constant rate (i.e. $\cfrac{dM}{dt}=$ constant), determine its instantaneous acceleration
$\color{green}{\text{Solution Steps – A}}$
Since there are no external forces in the horizontal direction, $P_{system,x,initial} = P_{system,x,final}$.
$\bullet$ In case of cannon, on a train (mass $M$), firing shells of mass $m$, at a relative velocity of $v_{rel}$ (with respect to the cannon, in its state before firing) in opposite direction to the motion of the train,
let’s say that the velocity of the cannon $+$ train system just before firing the first shell is $u$ towards the right and after firing the first shell, let’s say that the velocity of cannon+train (of mass $M-m$) is $v$,
which means that the velocity of shell will be $v_{rel}-u$ towards the left as seen by the observer on the ground,
Now, $P_i,x = P_f,x$, i.e linear momentum of cannon + train + shell system along the horizontal just before and just after the firing of the shell would remain the same, as there is no external force in the horizontal direction
So, $Mu=(M-m)v-m(v_{rel}-u)$, or, $V=\cfrac{(M-m)u+mv_{rel}}{M-m}$
$\bullet$ In case of a mass $m$, traveling through air and exploding into two (or more) fragments of masses $m_1$ and $m_2$, the momentum of this particle or system of fragments, during the explosion event will remain unchanged as there is no significant impulse acting on this system of particles during the small duration of explosion event.
Note that, while there is gravitational force $mg$ that is acting on this system, even during the explosion, impulse due to this force i.e. $mg \delta t$, can be neglected as duration of explosion event $\delta t$ is very small.
So, $\overrightarrow{P}_{system, \ i}$ (momentum before explosion) $=$ $\overrightarrow{P}_{system, \ f}$ (momentum after explosion)
$\color{green}{\text{Solution Steps – B}}$
In the direction of zero net external force, momentum will remain conserved, i.e. $m_1 u_1 + m_2 u_2 = (m_1 + m_2) v$, or, $v=\cfrac{m_1 u_1 + m_2 u_2}{m_1 + m_2}$
Note that in case of man jumping on buggy, if you are worried about the frictional force and resulting impulse that will act on the man+buggy system in the horizontal direction, remember that impulse due to frictional force would be negligible as long as the moment of inertia of wheels is relatively small.
$\color{green}{\text{Solution Steps – C}}$
If the system is gaining mass at the rate $\cfrac{dM}{dt}$, then for the duration $dt$, if we consider the system comprising of the spaceship of mass $M$ (at that instant) and dust particles of mass $dM$, then since there are no external forces, the linear momentum of the system will remain conserved over this time interval $dt$, i.e.
$Mu = (M+dM)(u+du)$ (assuming that dust particles are at rest initially)
or, $u dM = – M du$ (Ignoring the term dM du)
Now dividing both sides by differential time duration $dt$, we get
$a = \cfrac{du}{dt}$ $= – \cfrac{u}{M} \cfrac{dM}{dt}$ ($-ve$ sign implies deceleration)
$\color{blue}{\text{Important Question Type No. 18}}$
A) Given two masses undergoing elastic collision along $1-$dimension or $2-$dimensions, determine the unknowns (velocities or angles of deflection or maximum angle of deflection) using conservation of linear momentum (along 1 or 2 directions) and conservation of kinetic energy.
B) This may be followed by the kinetic energy of one of the masses getting converted into potential energy, in which case, establish the desired information about the final state, for example, the bob of the pendulum at rest is elastically hit by a mass and you might be asked to determine the maximum height that the bob of the pendulum would climb
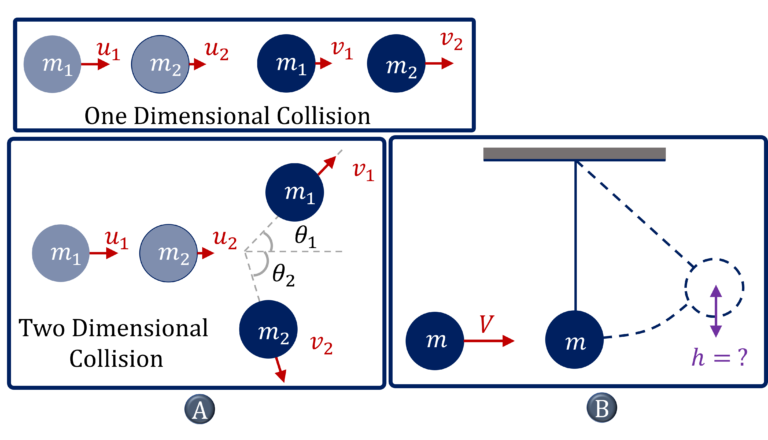
$\color{green}{\text{Solution Steps – A | One Dimensional Elastic Collision}}$
$\bullet$ If there is no (or negligible) impulse due to external forces in the direction of motion, the linear momentum of the system of colliding particles/masses would remain constant,
i.e. $m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2$ $\cdots$ $(1)$
$\bullet$ If the collision is elastic, mechanical energy, (i.e. elastic energy + kinetic energy) remains conserved during the collision meaning kinetic energy after the collision = kinetic energy before the collision
i.e. $\cfrac{1}{2} m_1 u_1^2 +$ $\cfrac{1}{2} m_2 u_2^2 =$ $\cfrac{1}{2} m_1 v_1^2 +$ $\cfrac{1}{2} m_2 v_2^2$ $\cdots$ $(2)$
From $(1)$ & $(2)$, we get,
$u_1 + v_1 = u_2 + v_2$ $\cdots$ $(3)$
Now, from $(1)$ & $(3)$, we can determine the unknown
Note that we can write $(3)$ as, $\cfrac{v_1 – v_2}{u_1 – u_2} = -1$ [Recall that the coefficient of restitution, $e=-$ $\cfrac{v_1 – v_2}{u_1 – u_2}$ is $1$ for elastic collisions]
Note that this definition of the coefficient of restitution is applicable for one dimensional collisions
$\color{green}{\text{Solution Steps – A | Two Dimensional Elastic Collision}}$
$\bullet$ If there is no (or negligible) impulse due to external forces in the plane of motion of particles, then the linear momentum of the system of colliding particles/masses would remain constant along both the dimensions
Along $x$: $m_1 u_1 + m_2 u_2 = m_1 v_1 \cos \theta_1 + m_2 v_2 \cos \theta_2$ $\cdots$ $(1)$
(Assuming that the two masses are initially travelling in the same direction, say $x$ direction)
Along $y$: $m_1 v_1 \sin \theta_1 = m_2 v_2 \sin \theta_2$ $\cdots$ $(2)$
$\bullet$ If the collision is elastic, mechanical energy, (i.e. elastic energy + kinetic energy) remains conserved during the collision meaning kinetic energy after the collision = kinetic energy before the collision
i.e. $\cfrac{1}{2} m_1 u_1^2 +$ $\cfrac{1}{2} m_2 u_2^2 =$ $\cfrac{1}{2} m_1 v_1^2 +$ $\cfrac{1}{2} m_2 v_2^2$ $\cdots$ $(3)$
From $(1)$, $(2)$ and $(3)$, we can find the desired unknown, (Note that we can only solve for 3 unknowns)
But if we are asked to determine the maximum angle of deviation for say mass $1$, given, $m_1$, $m_2$, $u_1$ and $u_2$, then resolve the above $3$ equations to obtain an equation in $v_1$ and $\theta_1$
$(m_1^2 + m_1 m_2) v_1^2 -$ $2(m_1 u_1 + m_2 u_2)m_1 \cos \theta_1 v_1 +$ $(m_1 u_1 + m_2 u_2)^2 – $ $(m_1 u_1^2 + m_2 u_2^2)m_2 = 0$
This is a quadratic equation in $v_1$, and for $v_1$ to have real roots, the determinant of this equation should be $\geq 0$, which will then give us the limits on angle $\theta_1$
$\color{green}{\text{Solution Steps – B}}$
Once we know the velocity of masses after the collision, we can use conservation of mechanical energy, if there are no other forces (other than the conservative forces) that are doing work on the mass of interest.
i.e. $\Delta U + \Delta K = 0$
$\color{blue}{\text{Important Question Type No. 19}}$
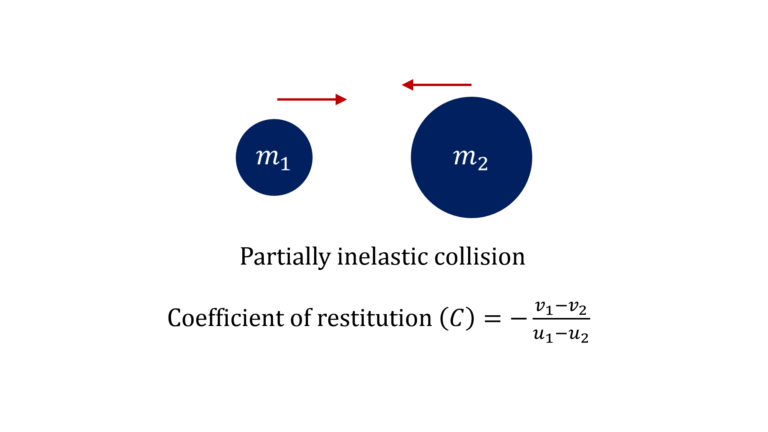
Partially inelastic collision meaning that the collision is neither elastic wherein both linear momentum and energy are conserved, nor, completely inelastic wherein linear momentum remains conserved but since the masses stick together after the collision, their velocities become the same after the collision.
$\color{green}{\text{Solution Steps}}$
In such partially inelastic collisions, only linear momentum remains conserved, meaning that we have only one equation to work with.
i.e. $m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2$
In such a scenario, to be able to determine $v_1$ and $v_2$, we might be provided with another equation in the form of coefficient of restitution for the partially inelastic collision
$e = – \cfrac{v_1 – v_2}{u_1 – u_2}$
or,
you might be provided some information on the kinetic energies of the masses after the collision
$\color{blue}{\text{Important Question Type No. 20}}$
There are 5 different ways questions, involving completely inelastic collision’ (wherein masses stick to each other after the collision, i.e. $e =0$), might be structured
–One dimensional completely inelastic collision–
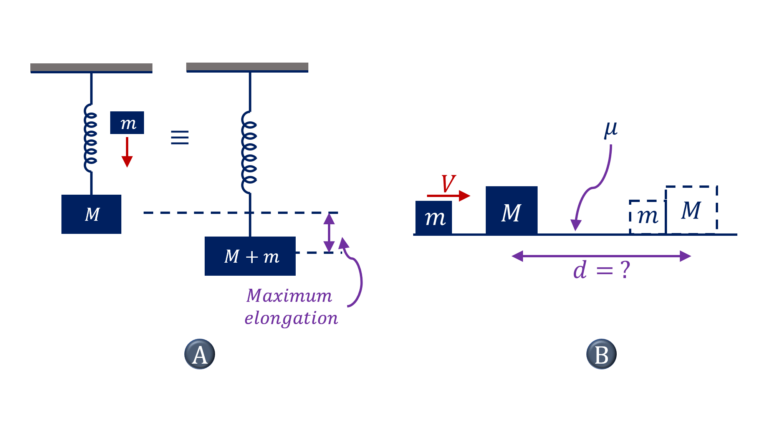
A) Given that there are a series of one-dimensional collisions between masses placed one after another, with some collisions being elastic and others being completely inelastic, determine the velocity of end mass or find the net loss in kinetic energy
B) Given one dimensional incompletely inelastic collision between two masses, either determine the information about the final position, for example, the compression or extension of the spring or the height the combined mass climbs to or the distance the combined masses travel on the rough surface before coming to a halt, using the work kinetic energy theorem
or
establish some information about the final velocity vector or time duration using the kinematics equations for the combined mass
–Two dimensional completely inelastic collision–
C) Given that two masses moving at an angle from each other undergo a completely inelastic collision, determine the initial angle between them (given their initial and final speeds) or the kinetic energy loss (given their initial ‘velocities’)
D) Given that two rigid bodies with smooth surfaces (for example, two smooth spheres) collide with their relative velocity at an angle from the normal to the contact surface (i.e. the line of action of impulse between them), and given that the coefficient of restitution $e$ is zero along the line of action of impulse, determine their final velocities
E) Given that two rigid bodies undergo a completely inelastic collision with motion obstructed in one direction say vertical direction and free along other, say along the horizontal direction, determine the loss in kinetic energy of the system (Note: Impulse between the two bodies has a component along the two directions).
$\color{green}{\text{Solution Steps-A}}$
$\bullet$ During a completely inelastic collision, linear momentum will remain conserved and the masses stick together afterward, which means, that they will move with the same velocity after the collision
i.e. $m_1 u_1 + m_2 u_2 = (m_1 + m_2)v$, where $u_1$ and $u_2$ are the initial velocities of the two masses undergoing completely inelastic collision and $v$ is their velocity after the collision
$\therefore$ $v = \cfrac{m_1 u_1 + m_2 u_2}{m_1 + m_2}$
$\color{green}{\text{Solution Steps-B}}$
$\bullet$ Once we know the velocity $v$ of the combined mass after the collision, we can use the work-kinetic energy theorem to determine the unknown
$W_{net} = \Delta K$
or
$W_{ext} + W_{conservative}= \Delta K$
or
Now, $\Delta U$ is defined as $\Delta U = – W_{conservative}$
or
$W_{ext} = \Delta U + \Delta K$
Please refer to the question types on the work kinetic theorem if you have any questions or doubts related to the work kinetic energy theorem.
$\color{green}{\text{Solution Steps-C}}$
Let’s say that the initial velocity vectors of masses $m_1$ and $m_2$ are $\overrightarrow{v}_{1,i}$ and $\overrightarrow{v}_{2,i}$ and let’s say the that the velocity vector of the combined mass is $\overrightarrow{v}_{f}$
Now, since there is no external force in the plane of motion of these 2 masses, linear momentum along two conveniently chosen mutually perpendicular directions $x$ & $y$ would be conserved,
i.e. $m_1 v_{1,i,x} + m_2 v_{2,i,x} = (m_1+m_2) v_f,x$
and
$m_1 v_{1,i,y} + m_2 v_{2,i,y} = (m_1+m_2) v_f,y$
Or, we can write these equations in terms of initial speeds of two masses, the angle between their initial velocities, final speed, and angle that the final velocity of the combined mass makes with, say, the initial direction of motion of $m_1$
5 variables, 2 equations. So the value of 3 of these 5 variables must be known for us to find unknown 2.
$\color{green}{\text{Solution Steps-D}}$
‘coefficient of restitution $e$ is zero along the line of action of impulse’, implies that the component of final velocities of the two masses along the line of action of impulse are the same (though they don’t stick together after collision)
$\color{green}{\text{Solution Steps-E}}$
Linear momentum of the system will only be conserved in the direction along which there is no external impulse on the system of colliding masses
$\color{blue}{\text{Important Question Type No. 22}}$
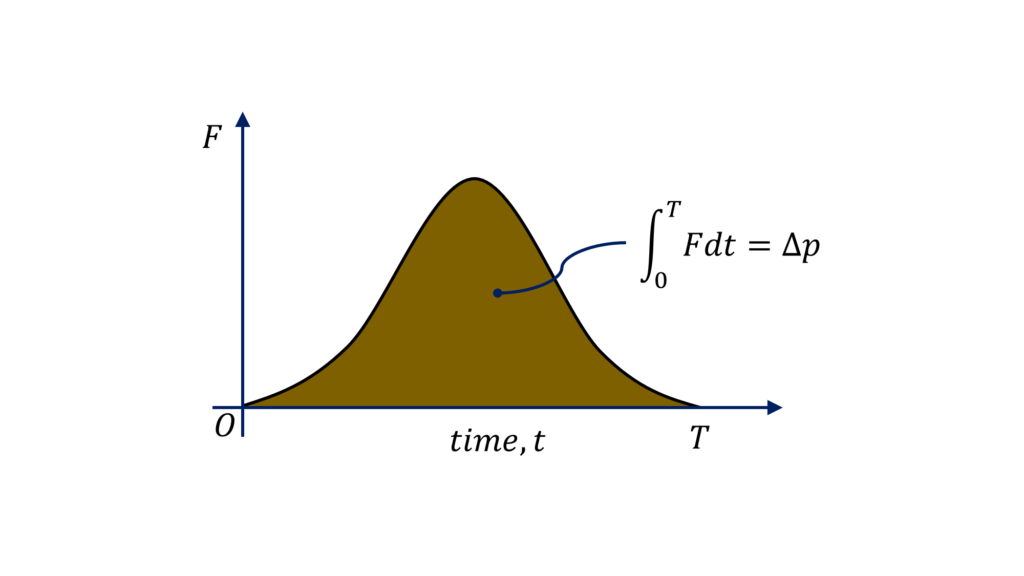
A) Given a constant force or given a force as a function of time $t$, determine the change in momentum of a particle over a given time duration $t$ (time duration may be provided indirectly)
B) For a particle undergoing collision with a wall, given $\overrightarrow{v}_i$ and $\overrightarrow{v}_f$ (in two dimensions), determine impulse due to normal force or the frictional force.
$\color{green}{\text{Solution Steps – A}}$
One Dimensional Scenario:
$\Delta p = \int_0^{\Delta t} F dt$
Two or Three Dimensional Scenario
$\Delta p_x = \int_0^{\Delta t} F_x dt$
$\Delta p_y = \int_0^{\Delta t} F_y dt$
$\Delta p_z = \int_0^{\Delta t} F_z dt$
$\color{green}{\text{Solution Steps – B}}$
Impulse due to normal force would be $=\Delta p_{\perp}$ in the direction perpendicular to the wall
Impulse due to tangential or frictional force would be $=\Delta p_{\parallel}$ in the direction parallel to the wall
$\color{green}{\text{Solution Steps}}$
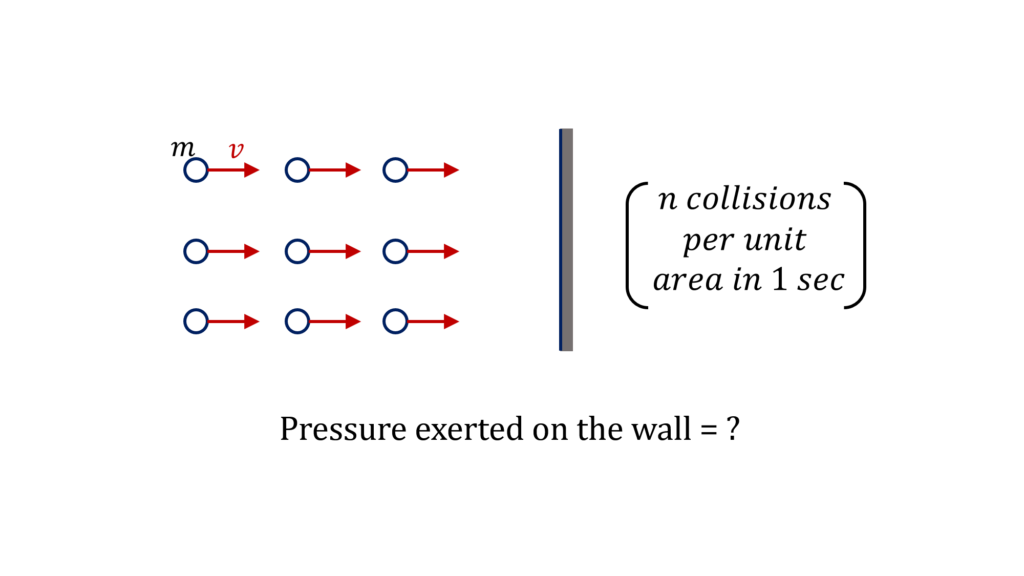
$\bullet$ Impulse exerted on the wall per unit area over 1 sec $=$ Impulse exerted by $1 \ m^2$ of the wall on the particles in one second which is equal to change in momentum of the particles striking $1 \ m^2$ area in $1 \ sec$
$\bullet$ Change in the momentum of the particles striking 1m^2 area in one sec $= 2nmv$ (recall that the collision is elastic)
$\bullet$ $F_{average}$ (per unit area) $\times 1 \ sec = 2nmv$
$\bullet$ Pressure, $p = 2nmv$
For all question types that you can expect in JEE Advanced and JEE Main, please purchase ‘Rankers Choice‘




