There are 24 questions, each carrying equal marks (4 marks each).
Time alloted is 2 hours
Maximum Marks = 96
Subjective Questions (1 to 3)
1. For the arrangement shown, a cylinder of mass $m$ with cross sectional area $A$, initially in equilibrium position, is displaced slightly inside the liquid of density $\rho$. Prove that the motion is simple harmonic and also find its time period.
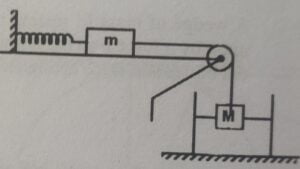
Correct Answer is $T = 2 \pi \sqrt{\cfrac{2m}{k + A \rho g}}$
Let’s say that at equilirbium, length $l$ of the cylinder is immersed in liquid and spring is stretched by a length $d$, which means
$T = mg – \rho A l g = kd$ (i)
Now, let’s say that we displace cylinder slightly downwards by distance $x$, then writing newton’s 2nd law for the two masses will give us
Cylinder:
$T – mg – \rho A (l + x) = – m \cfrac{dx^2}{dt^2}$ $\cdots$ (ii)
Other mass $m$:
$k(d+x) – T = -m \cfrac{dx^2}{dt^2}$ $\cdots$ (iii)
Adding the (ii) and (iii) and using (i) we get
$(k + \rho A) x = – 2m \cfrac{dx^2}{dt^2}$
or natural frequency $\omega$ $= \sqrt{\cfrac{k + \rho A}{2m}}$
or $T = 2 \pi \sqrt{\cfrac{2m}{k + A \rho g}}$
2. A block of mass $m = 1$ Kg is attached to a free end of a spring whose end is fixed with a wall as shown in the figure. The block is performing simple harmonic motion. The position of the block from $O$ is given by $x = 2 + \cfrac{1}{\sqrt{2}} \sin 2t$, where $x$ is in meter and $t$ is in second. A particle of same mass is released from the circular path at a height $h = 80$ cm, then particle collides and sticks to the block. The collision takes place when velocity of the block is zero and spring is elongated. Find
(i) Time period of new SHM.
(ii) Maximum velocity of the system
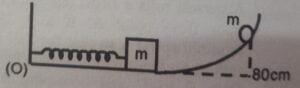
Correct answer is
(i) $\pi \sqrt{2}$ sec
(ii) $\sqrt{5} m/s$
Just after the collision, velocity of mass $2m = 2$ Kg will be
$m \sqrt{2gh} = 2m v$ or $v = \sqrt{\cfrac{gh}{2}}$
so, total mechanical energy of the spring ($k$) – mass ($2m$) system becomes $\cfrac{1}{2} k (\cfrac{1}{\sqrt{2}})^2 + \cfrac{1}{2} 2m v^2$ $= \cfrac{k}{4} + \cfrac{mgh}{2}$ where $\cfrac{k}{m} = \omega^2 = 4$ or $k = 4m = 4$ N/m
so time period of new SHM will be $\cfrac{2 \pi}{\omega^{‘}} = \cfrac{2 \pi}{\sqrt{\cfrac{k}{2m}}}$ $=\cfrac{2 \pi}{\sqrt{2}} = \sqrt{2} \pi$
As for the maximum velocity, using the energy that the total mechanical energy is conserved, we can write
$\cfrac{1}{2} 2m v_{max}^2 = \cfrac{k}{4} + \cfrac{mgh}{2}$
or $v_{max} = \sqrt{5}$ m/s
3. Two blocks $A$ and $B$ of masses $m$ and $2m$ respectively are connected together by a light spring of stiffness $k$ and then placed on a smooth horizontal surface. The blocks are pushed towards each other such that spring gets compressed by a length $x_0$ and then released from rest. Find the work done on the block $A$ by the spring, by the time the spring aquires its natural length.
Correct answer is $\cfrac{1}{3} k x_0^2$
Multiple choice questions (Only one correct) (4 to 14)
4. Three simple harmonic motions in the same direction having same amplitude and the same period are superposed. If each differs in phase from the next by $\pi / 2$, then which of the following is wrong
(i) Resultant amplitude is $(\sqrt{2} + 1) a$
(ii) Phase of resultant motion relative to first is $90^{\circ}$
(iii) The energy associated with the resultant motion is 3 times the energy associated with any single motion.
(A) (i) & (iii)
(B) (ii) only
(C) (ii) & (iii)
(D) (i), (ii) & (iii)
Correct answer is (A)
5. A uniform semi-circular disc of mass $m$ and radius $r$ is suspended as shown in the figure. If $T$ is the time period of small oscillations about an axis passing through point of suspension and perpendicular to plane of disk. Then $T$ is equal to
(A) $2 \pi \sqrt{\cfrac{3r}{8g}}$
(B) $2 \pi \sqrt{\cfrac{3r \pi}{8g}}$
(C) $2 \pi \sqrt{\cfrac{2r \pi}{9g}}$
(D) $2 \pi \sqrt{\cfrac{2r}{9g}}$
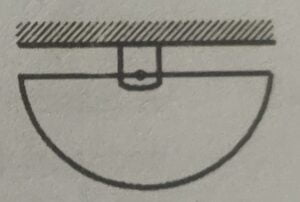
Correct answer is (B)

Center of mass of uniform semi-circular disc is located at $\cfrac{4r}{3 \pi}$ from the center of curvature
So if we displace the disc from its mean or equilibrium position by an angle $\theta$, then the restoring torque would be
$\tau = mg \cfrac{4r}{3 \pi} \sin \theta$
For small angle $\theta$, $\sin \theta \approx \theta$
or $\tau = mg \cfrac{4r}{3 \pi} \theta$
So newton’s 2nd law $\tau = I \alpha$, can we written as
$- mg \cfrac{4r}{3 \pi} \theta = I \cfrac{d^2 \theta}{dt^2}$
where moment of inertia $I = \cfrac{1}{2} mr^2$
so, $\omega = \sqrt{\cfrac{8g}{3r \pi}}$
6. Four simple harmonic vibrations $y_1 = 8 \sin \omega t$, $y_2 = 6 \sin (\omega t + \pi/2)$, $y_3 = 4 \sin (\omega t + \pi)$, $y_4 = 2 \sin (\omega t + 3 \pi/2)$ are superimposed on each other. The resulting amplitude and phase are respectively.
(A) $4 \sqrt{2}$ and $\tan^{-1} (1)$
(B) $4 \sqrt{2}$ and $\tan^{-1} (6/8)$
(C) $20$ and $\tan^{-1} (1/2)$
(D) $20$ and $\tan^{-1} (2)$
Correct answer is (A)
7. A point mass $m$ is displaced slightly from point $O$ and released. It is constrained to move along parabolic path having equation $x^2 = ky$, then its angular frequency of oscillation is:
(A) $\sqrt{\cfrac{g}{2k}}$
(B) $\sqrt{\cfrac{2g}{k}}$
(C) $\sqrt{\cfrac{g}{k}}$
(D) $\sqrt{\cfrac{3g}{2k}}$
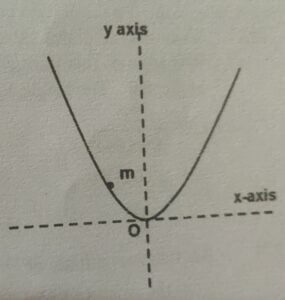
Correct answer is (B)
8. The displacement of two identical particles executing SHM are represented by equations $x_1 = 4 \sin [10t + (\pi /6)]$ and $x_2 = 5 \cos \omega t$. For what value of $\omega$, will the energy of both the particles be same?
(A) $16$ units
(B) $6$ units
(C) $4$ units
(D) $8$ units
Correct answer is (D)
9. A block of mass $m$ is attached to a spring of force constant $k$ whose other end is fixed to a horizontal surface. Initially the spring is in is natural length and the block is released from rest. The average force acting on the surface by the spring till the inistant when the block has zero acceleration for the first time is
(A) $\cfrac{mg}{\pi}$
(B) $\cfrac{2mg}{\pi}$
(C) $\cfrac{3mg}{\pi}$
(D) $\cfrac{4mg}{\pi}$
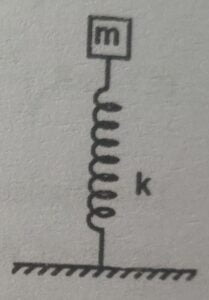
Correct answer is (B)
10. In the figure shown surfaces are smooth and blocks $A$ and $B$ have same mass $m$. The two bodies are displaced right and released. It is found that bodies move according to the equation $x_A = A \sin (\omega t + \phi)$, $x_B = 2A \sin (\omega t + \phi)$
(A) $\cfrac{K_1}{K_2} = \cfrac{3}{2}$
(B) $\cfrac{K_1}{K_2} = \cfrac{1}{2}$
(C) $\cfrac{K_1}{K_2} = 1$
(D) $\cfrac{K_1}{K_2} = 2$
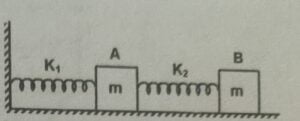
Correct answer is (A)
11. A block of mass $m$ lie on horizontal smooth surface and connected with the springs at their natural length as shown in figure. When block is slightly displaced, then find the time period of oscillation.
(A) $\cfrac{\pi}{4} \sqrt{\cfrac{m}{7k}}$
(B) $2 \pi \sqrt{\cfrac{m}{7k}}$
(C) $3 \pi \sqrt{\cfrac{m}{7k}}$
(D) $\cfrac{\pi}{2} \sqrt{\cfrac{m}{7k}}$
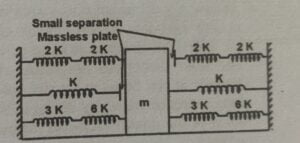
Correct answer is (B)
12. A triangular rigid wire frame ‘$AOB$’ is made, in which length of each wire is $l$ and mass is $m$. The whole system is suspended from point ‘$O$’ and free to perform SHM about $x-$axis or about $z-$axis. When it performs SHM about $x-$axis its time period of oscillation is $T_1$ and when it performs SHM about $z-$axis, its time period of oscillation is $T_2$, then choose the correct option.
(A) $T_1 < T_2$
(B) $T_1 > T_2$
(C) $T_1 = T_2$
(D) None
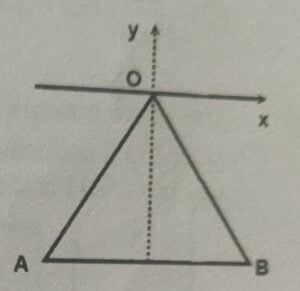
Correct answer is (A)
13. A rod of mass $m$ and length $L$ is kept on a horizontal smooth surface. The rod is hinged at its one end $A$. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant $k$ is rigidly attached to the lower end of rod and spring of spring constant $12k$ just touches the rod at its midpoint $C$, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small oscillation of the rod will be
(A) $\pi \sqrt{\cfrac{m}{}3k}$
(B) $\cfrac{3 \pi}{2} \sqrt{\cfrac{m}{3k}}$
(C) $\pi [\sqrt{\cfrac{m}{3k}} + \sqrt{\cfrac{3g}{2L}}]$
(D) $\cfrac{3 \pi}{2} [\sqrt{\cfrac{m}{3k}} + 4 \sqrt{\cfrac{3g}{2L}}]$
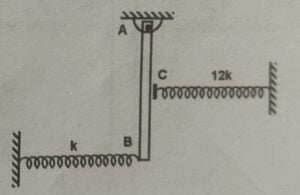
Correct answer is (B)
14. A bar of mass $m$ is sispended horizontally on two vertical springs of spring constant $k$ and $3k$. The bar bounces up and down while remaining horizontal. Find the time period of oscillation of the bar (neglect mass of springs and friction everywhere)
(A) $2 \pi \sqrt{\cfrac{m}{k}}$
(B) $2 \pi \sqrt{\cfrac{m}{3k}}$
(C) $\pi \sqrt{\cfrac{2m}{3k}}$
(D) $\pi \sqrt{\cfrac{3m}{4k}}$
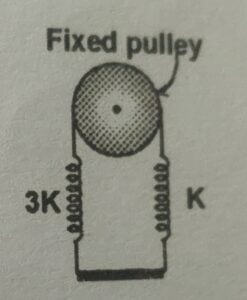
Correct answer is (B)
Assertion and Reason (15 to 16)
15. $\textbf{STATEMENT-1}$
A pendulum bob is suspended from a fixed support through a string of length $l$. It is executing simple harmonic motion of small amplitude. A person running with an aeleration $a$ on the horizontal floor will observe the time period of the pendulum to be $2 \pi \sqrt{\cfrac{l}{\sqrt{a^2 + g^2}}}$
$\textbf{STATEMENT-2}$
In a frame attached to the person the bob will experience a pseudo force
(A) Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-I.
(B) Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
(C) Statement-1 is True, Statement-2 is False.
(D) Statement-1 is False, Statement-2 is True.
Correct answer is (D)
16. $\textbf{STATEMENT-1}$
The motion of a simple pendulum is not simple harmonic for large amplitudes
$\textbf{STATEMENT-2}$
The restoring torque on a simple pendulum about the point of suspension is proportional to $\sin \theta$, where $\theta$ is the angular displacement of the pendulum
(A) Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-I.
(B) Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
(C) Statement-1 is True, Statement-2 is False.
(D) Statement-1 is False, Statement-2 is True.
Correct answer is (A)
Multiple Choice Questions (One or more than one correct answers) (17 to 19)
17. A certain rough platform is performing oscillations given by $y_p = A \sin \omega t \hat{j}$, while another block kept on the platform performs oscillations on the platform given by $x_B = A \cos \omega t \hat{i}$, as seen from the ground.
(A) The direction of frictional force on the block will always be opposite to its velocity relative to the platform
(B) The direction of frictional force on the block will be always opposite to its relative acceleration w.r.t platform
(C) The direction of frictional force on the block at any instant will be $\cos (\omega t) \hat{i} + \sin (\omega t) \hat{j}$
(D) Direction of friction at any instant will be $\sin (\omega t) \hat{i} + \cos (\omega t) \hat{j}$
Correct answers are (A) & (C)
18. A particle executes simple harmonic motion between $x = – A$ and $x = + A$. The time taken for it to move from $x=0$ to $x = \cfrac{A}{2}$ is $T_1$ and to move from $x = \cfrac{A}{2}$ to $x = \cfrac{A}{\sqrt{2}}$ is $T_2$. Then
(A) $T_1 < T_2$
(B) $T_1 = T_2$
(C) $T_1 = 2 T_2$
(D) $T_2 = 2 T_1$
Correct answer is (C)
19. A cylindrical block of density $d$ stays fully immersed in a beaker filled with two immiscible liquids of different densities $d_1$ and $d_2$. THe block is in equilibrium with half of it in liquid 1 and the other half in liquid 2. If the block is given small downward displacement, neglecting frictional losses, then
(A) it executes simple harmonic motion
(B) its motion is oscillatory but not SHM
(C) frequency of oscillation depends on size of the cylinder
(D) displacement of center of cylinder is symmetric about its equilibrium position

Correct answers are (A) & (D)
Comprehension (20 to 22)
Read the paragraph carefully and answer the following questions:
The plates each of area $A$ of a parallel plate capacitor are given charges $Q$ and $-Q$. The plates are joined by a non-conducting spring of force constant $k$. The natural length of the spring is $d$, the initial separation between the plates. The left plate is connected to a vertical wall through a massless non-conducting rope and the right plate is connected to a block of mass $m$ through similar rope. Assume the pulley to be massless, neglect dielectric effect of the spring and $Q^2 < 2 m A \epsilon_0 g$.

20. If the block is released from rest, the maximum elongation of the spring is
(A) $\cfrac{2}{k} (mg – \cfrac{Q^2}{A \epsilon_0})$
(B) $\cfrac{2}{k} (mg – \cfrac{2Q^2}{A \epsilon_0})$
(C) $\cfrac{2}{k} (mg – \cfrac{Q^2}{2A \epsilon_0})$
(D) None of these
Correct answer is (C)
Since there are no dissipative forces and no external force is acting on the system, other than electrostatic and gravitational forces, the total mechanical energy of the system will remain conserved
i.e. $\Delta U + \Delta K = 0$
or simply $\Delta U = 0$, as $K$ is zero initially and at the maximum stretch
i.e. $-mg \delta_{max} + \cfrac{Q^2}{2C’} – \cfrac{Q^2}{2C} + \cfrac{1}{2} k \delta_{max}^2 = 0$
where $\delta_{max}$ is the maximum extension and capacitances, $C = \cfrac{\epsilon_0 A}{d}$ and $C’ = \cfrac{\epsilon_0 A}{d + \delta_{max}}$
so, $-mg \delta_{max} + \cfrac{Q^2}{2 \epsilon_0 A} \delta_{max} + \cfrac{1}{2} k \delta_{max}^2 = 0$
or $\delta_{max} = \cfrac{2}{k} (mg – \cfrac{Q^2}{2A \epsilon_0})$
21. If $T$ be the time period of oscillation, then
(A) $T > 2 \pi \sqrt{\cfrac{m}{k}}$
(B) $T < 2 \pi \sqrt{\cfrac{m}{k}}$
(C) $T = 2 \pi \sqrt{\cfrac{m}{k}}$
(D) $T$ will be dependent on $Q$
Correct answer is (C)
At the equilibrium position,
$k \delta + Q\cfrac{\sigma}{2 \epsilon_0} = mg$
where $\delta$ is the extension of spring when the system is at equilibrium
Now if we displace mass from this equilibrium position by a small distance $x$ (say in the downwards direction) then, the restoring force on mass $m$ would be given by
$T – mg$, where $T$ can be determined using newton’s 2nd law for the massless right capacitor, i.e.
$T – k (\delta + x) – Q\cfrac{\sigma}{2 \epsilon_0} = 0$
or the restoring force $= kx$
So newton’s 2nd law for mass $m$ will give us
$-kx = m \cfrac{d^2 x}{dt^2}$
or $T = 2 \pi \sqrt{\cfrac{m}{k}}$
22. If $Q^2 = 2 m A \epsilon_0 g$, the elongation of the spring is
(A) zero
(B) $\cfrac{2}{k} (mg – \cfrac{Q^2}{A \epsilon_0})$
(C) $\cfrac{2}{k} (2mg – \cfrac{Q^2}{A \epsilon_0})$
(D) None of these
Correct answer is (A)
Numerical Type Questions (23 to 24)
23. Find the natural frequency of the system shown in the figure. The pulleys are smooth and massless (Given $\cfrac{k}{m} = 2 \pi^2$).
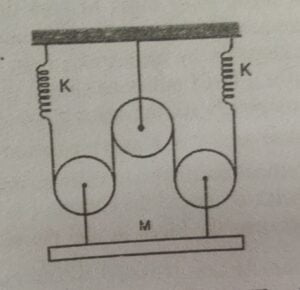
Correct answer is 2
Let’s say that mass $m$ is displaced downwards by a small distance $x$ from its mean or equilibrium position
This means that the vertical distance between the top, fixed pulley and two bottom pulleys has increased by $x$ or there is an additional string length of $4x$, which then implies that the springs are stretched by an additional distance of $2x$
So increase in tension in the string is $2kx$
or the restoring force on mass $m$ is $4 \times 2 kx$ $= 8kx$
So writing the newton’s 2nd law for mass $m$, we get,
$-8kx = m \cfrac{d^2x}{dt^2}$
$\implies$ $\omega = \sqrt{\cfrac{8k}{m}}$ $=4 \pi$
or natural frequency $f= \cfrac{\omega}{2 \pi}$ $= 2$
24. Three infinitely long thin wires each carrying current $I$ in the same direction are in $x-y$ plane of a gravity free space. The central wire is along the $y-$axis while the other two are along $x = \pm d$. If the central wire is slightly displaced along z-axis and released, show that it will execute S.H.M. The linear mass density of the wire is $\lambda$. If the time period of this small oscillation is $\cfrac{k\pi d}{I} \sqrt{\cfrac{\pi \lambda}{\mu_0}}$, then find the value of $k$.
Correct answer is 2

If we displace the middle wire by a small distance $z$ along the +ve z-axis, then the net magnetic field $B_{net}$ $= 2 \cfrac{\mu_0 I}{2 \pi \sqrt{z^2 + d^2}} \sin \theta$ will act along the $x-$axis
For small $z$, $\sin \theta \approx \theta = \cfrac{z}{d}$
or $B_{net}$ $= \cfrac{\mu_0 I}{\pi d^2} z$
Now, magnetic force on a current carrying wire is given by $\overrightarrow{F}_b = i \overrightarrow{dL} \times \overrightarrow{B}$
so the restoring force on the central wire would be towards $-z$ axis and the magnitude of restoring torque on a unit length of the wire would be
$F = \cfrac{\mu_0 I^2}{\pi d^2} z$
so expression for newton’s 2nd law would become
$- \cfrac{\mu_0 I^2}{\pi d^2} z = \lambda \cfrac{d^2 z}{dt^2}$
or $\omega = \cfrac{I}{d} \sqrt{\cfrac{\mu_0}{\pi \lambda}}$
and $T = \cfrac{2 \pi}{\omega}$

