Equation of trajectory of a projectile
Recall, the equations of motion of the projectile for horizontal and vertical direction
Horizontal Direction : $x = u_x t$ $=u \cos \theta t$
Vertical Direction : $y = u_y t -$ $\cfrac{1}{2} gt^2$ $=u \sin \theta -$ $\cfrac{1}{2} gt^2$
Since we want the equation of trajectory $y = f(x)$, let’s go ahead and eliminate time variable $t$ from the two equations which gives us $y = \tan \theta x – \cfrac{g}{2u^2 \cos^2 \theta} x^2$
Now, let’s say that you have been given the equation of trajectory of the projectile as $y =$ $ax -$ $bx^2$, can you determine angle of projection, maximum height and range
Angle of Projection = $\left.\cfrac{dy}{dx}\right|_{t=0}$
Maximum Height: Find $x_{top}$ for which $\cfrac{dy}{dx} =0$, then maximum height, $H=$ $ax_{top}$ $- bx_{top}^2$
Range: Find $x$ for which $y=0$ (other than $x=0$) and that will be the range
With that, now let’s find out the radius of curvature at different points along the trajectory.
Projectile Motion | Important Questions | JEE PYQs
- Types of projectile motion
- Equations of projectile motion
- Range of a projectile
- Maximum height of a projectile
- Trajectory of a projectile
- Radius of curvature of projectile
- Velocity of projectile at time $t$ or height $h$
- Projectile Motion Examples
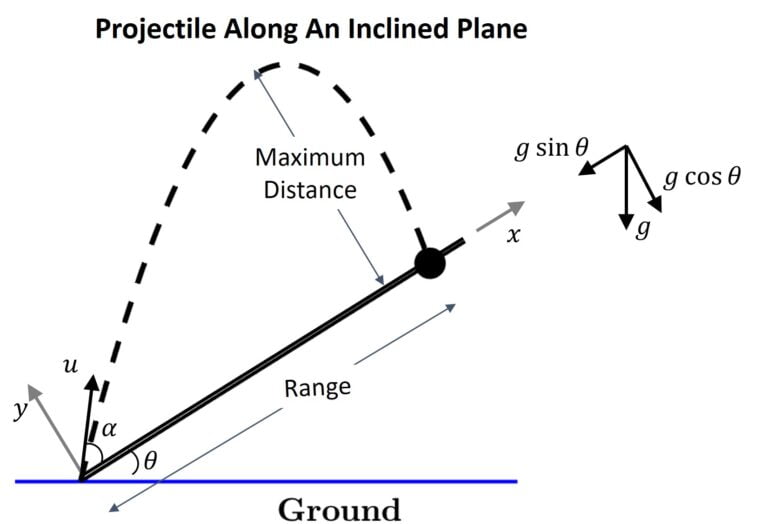
- Projectile motion along an inclined plane
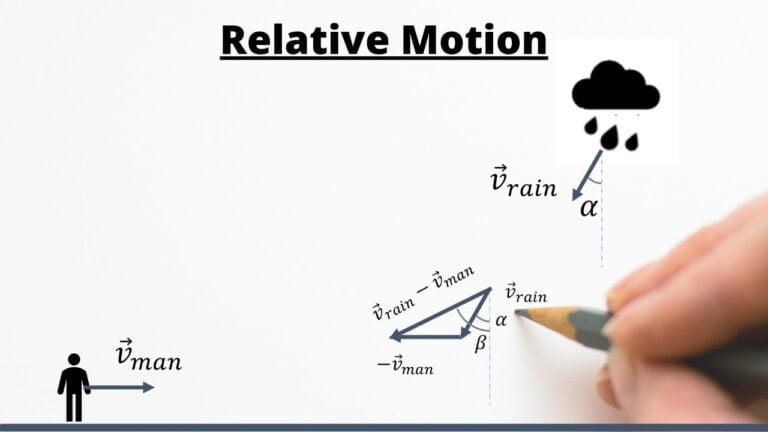
- Relative motion of projectile(s)
Kinematics Overview – What you need to know for JEE Main and JEE Advanced