Radius of trajectory of a projectile at a point along it’s trajectory is the radius of circular arc which best approximates the curve at that point and tells us how the trajectory of the projectile is curving at that point.
For example, smaller radius of curvature at the top (i.e. at the point of maximum height) means it curves more at the top, than say, at the launch or landing point where it curves less.
So, before we go through the steps to determine the radius of curvature at some point along the trajectory of the projectile, let’s visualize the radius of curvature
Finding radius of curvature of projectile
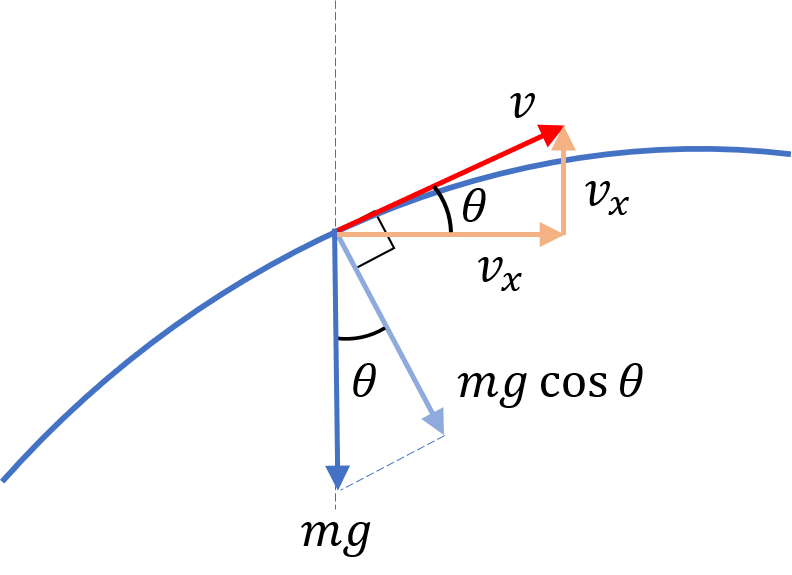
So how do we determine the radius of curvature of the trajectory at any point along the trajectory?
Well, note that what is changing the direction of velocity vector of the projectile at the point of interest is the component of force perpendicular to velocity vector (the component of force in the direction of the velocity vector will cause the change in the magnitude of the velocity vector)
Now, the only force acting on the projectile is the gravitational force $mg$, pointed vertically downwards and as we can tell from the figure above, the component of gravitational force perpendicular to velocity vector is $mg \cos \theta$
And what is the angle $\theta$ that the velocity vector makes with the horizontal at the point of interest along the trajectory? Well, we can find that using the relation $\tan \theta = \cfrac{v_y}{v_x}$ or $\cos \theta = \cfrac{v_x}{\sqrt{v_x^2 + v_y^2}}$
So, using newton’s law along the normal to the trajectory, $mg \cos \theta = \cfrac{mv^2}{R}$ or $R = \cfrac{v^2}{g \cos \theta}$
Radius of curvature at maximum height
At maximum height, angle that the velocity vector makes with the horizontal, $\theta = 0$.
So, radius of curvature at maximum height $=\cfrac{u^2 \cos^2 \theta}{g}$.
With that we will now establish velocity of the projectile at different point in time or at different points along the trajectory. And during this discussion, we will also explore the average velocity of the projectile between any two points along the trajectory
Projectile Motion | Important Questions | JEE PYQs
- Types of projectile motion
- Equations of projectile motion
- Range of a projectile
- Maximum height of a projectile
- Trajectory of a projectile
- Radius of curvature of projectile
- Velocity of projectile at time $t$ or height $h$
- Projectile Motion Examples
- Projectile motion along an inclined plane
- Relative motion of projectile(s)
Kinematics Overview – What you need to know for JEE Main and JEE Advanced