Velocity of projectile at any instant can be written, in the vector form, as $\overrightarrow{v}(t) =$ $v_x \hat{i} +$ $v_y \hat{j}$, where $v_x$ is the $x$ component of velocity vector $\overrightarrow{v}(t)$ at time $t$ and $v_y$ is its $y$ component at that time.
So let’s see, what will this expression be, in terms of initial speed $u$ and projection angle $\theta$.
Velocity of projectile at any instant
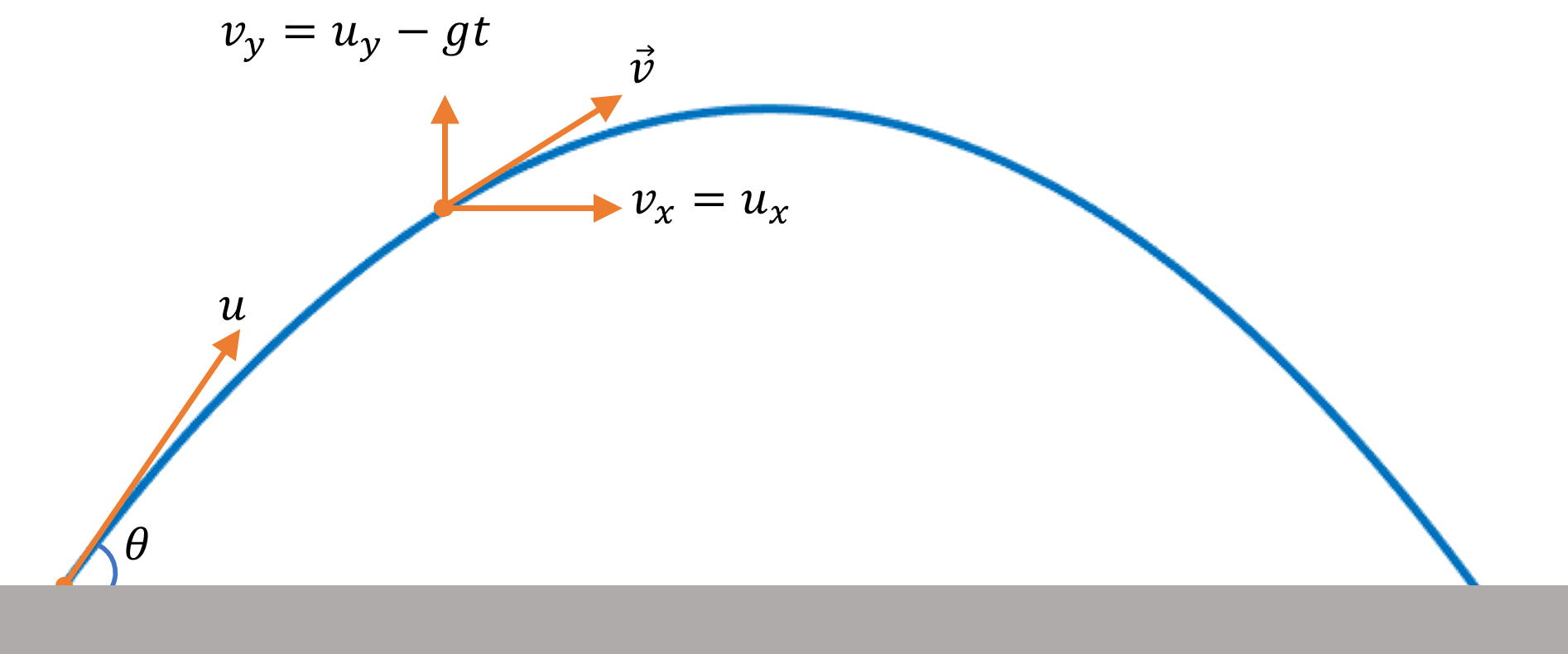
Now, $v_x$, $x$ component of velocity vector $\overrightarrow{v}(t)$ is simply $=u_x=$ $u \cos \theta$, as there is no acceleration in the horizontal direction.
As for $v_y$, $y$ component of velocity vector $\overrightarrow{v}(t)$, $v_y =$ $u_y – gt$ $=u \sin \theta – gt$
So, velocity vector $\overrightarrow{v}(t)$ will simply be $=u \cos \theta \hat{i} +$ $(u \sin \theta – gt)$ $\hat{j}$
Velocity of projectile at 'half' of maximum height
Now, let’s determine the expression for velocity vector $\overrightarrow{v} =$ $v_x \hat{i} +$ $v_y \hat{j}$ at height $y$.
So, at height $h$, $v_x$, $x$ component of velocity vector $\overrightarrow{v}$ is simply $=u_x=$ $u \cos \theta$, as there is no acceleration in the horizontal direction.
As for $v_y$, recall that $v_y^2 = u_y^2 – 2gy$ $= u^2 \sin^2 \theta – 2gy$, so $v_y=$ $\pm \sqrt{u^2 \sin^2 \theta – 2gy}$. Note that projectile is at height $h$ twice during it’s slight (once on the way up and once on the way down and hence $\pm$)
$\therefore$ velocity vector $\overrightarrow{v}(y)$ will simply be $=u \cos \theta \hat{i} $ $\pm \sqrt{u^2 \sin^2 \theta – 2gy} \hat{j}$
So, what will the velocity of projectile be at ‘half’ the maximum height, i.e. at $y = \cfrac{H}{2}$, where maximum height $H=\cfrac{u^2 \sin^2 \theta}{2g}$
Well, that will simply be $=u \cos \theta \hat{i} $ $\pm \cfrac{u \sin \theta}{\sqrt{2}} \hat{j}$ or speed at that point will be $\sqrt{\cfrac{1+u^2 \cos^2 \theta}{2}}$.
The speed of a projectile at its maximum height
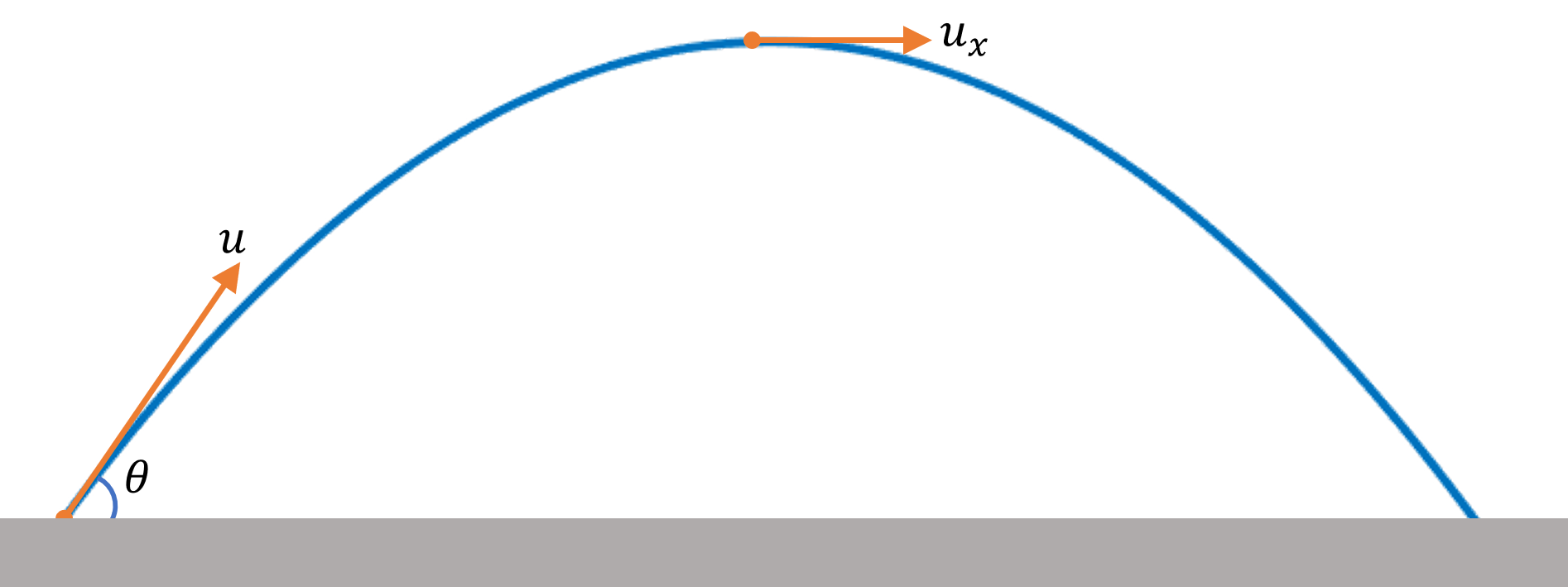
Well at maximum height $H$, $y$ component of velocity vector becomes zero, so $\overrightarrow{v}(H)=u \cos \theta \hat{i}$.
With that, now let’s determine the average velocity vector of a projectile for two scenarios: 1) over a symmetric part of the journey, meaning, between two points at same height 2) over non-symmetric part of the journey, meaning average velocity between two points that are at different heights.
Average velocity of a particle in projectile motion (symmetric)
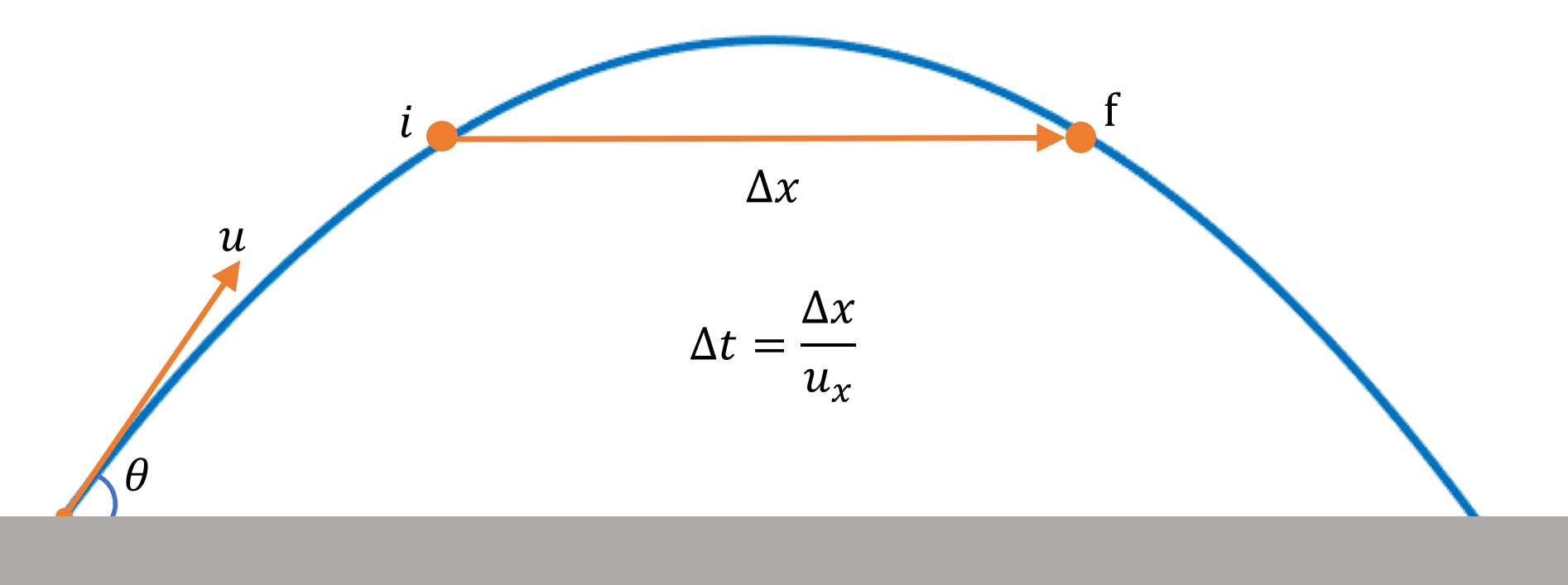
So, starting with average velocity over a symmetric part of the journey, meaning, average velocity between two points located at the same height, say for example, landing and launch points, at ground level.
Recall that average velocity is defined as $=\cfrac{Net \ Displacement}{Time \ Duration}$ $=\cfrac{\overrightarrow{r}_f – \overrightarrow{r}_i}{\Delta t}$
For points located at same height,
$\overrightarrow{r}_f – \overrightarrow{r}_i=$ $(x_f – x_i) \hat{i}$ and $\Delta t$ between $x_f$ and $x_i$ is simply $=\cfrac{x_f – x_i}{u \cos \theta}$
so, $\overrightarrow{v}_{avg} = u \cos \theta \hat{i}$
Average velocity over a non-symmetric part of the journey
As for average velocity over a non symmetric part of the flight, meaning, average velocity between two points at different heights, it can be calculated using the definition $\overrightarrow{v}_{avg} =$ $\cfrac{\overrightarrow{r}_f – \overrightarrow{r}_i}{\Delta t}$.
When is the velocity at the maximum height of a projectile, half its initial velocity?
Speed at the maximum height of a projectile, $u \cos ]theta$, will be half its initial speed, $u$, when $\cos \theta = \cfrac{1}{2}$ or $\theta = 60^\circ$.
Projectile Motion | Important Questions | JEE PYQs
- Types of projectile motion
- Equations of projectile motion
- Range of a projectile
- Maximum height of a projectile
- Trajectory of a projectile
- Radius of curvature of projectile
- Velocity of projectile at time $t$ or height $h$
- Projectile Motion Examples
- Projectile motion along an inclined plane
- Relative motion of projectile(s)
Kinematics Overview – What you need to know for JEE Main and JEE Advanced