For a cube of equal resistance along its edges, let’s determine the equivalent resistance between
- two vertices along the body diagonal
- two vertices along the face diagonal
- two adjacent vertices
Note that we will explore two methods here: (a) Equivalent circuit, utilizing symmetry (b) Potential method
1. Cube Resistance Problem | Equivalent resistance between two vertices along the 'body' diagonal
Approach 1 : Equivalent circuit, utilizing symmetry
Equivalent resistance between two vertices along the body diagonal is $= \cfrac{5R}{6}$. The equivalent representations are shown below which will help you understand the approach. Note that vertices $B$, $D$, and $E$ are at the same potential because of symmetry and similarly $C$, $F$ and $H$ are at the same potential.



Approach 2 : Current Method
Assume that the current flowing into vertex $A$ is $i$. Now because of the symmetry we can assign the current in different branches as follows
Now, to establish Potential difference, $V_{AG}$, between vertices $A$ and $G$ let’s follow the path $A – B – C – G$ and let’s write down the potential drop
So, $V_{AG} = \cfrac{i}{3} R + \cfrac{i}{6} R + \cfrac{i}{3} R$ $= \cfrac{5R}{6} i$
So $R_{eq} = \cfrac{V_{AG}}{i} = \cfrac{5R}{6}$

2. Cube Resistance Problem | Equivalent resistance between two vertices along the 'face' diagonal
Approach 1 : Equivalent circuit
Equivalent resistance between two vertices along the face diagonal is $= \cfrac{3R}{4}$. The equivalent representations are shown below which will help you understand the approach.
Note that circuit is symmetric about $B-F-H-D$ as inidicated by red dotted line, meaning all these vertices are at the same potential which helps us simplify the circuit as shown below



Approach 2 : Potential Method
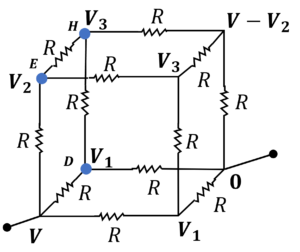
Having assigned potentials to different vertices (taking into account the symmetry), we will now write the junction rule for vertices $D$, $E$ and $F$, which will give us 3 equations in 3 unknowns, namely, $V_1$, $V_2$ and $V_3$
So, writing the junction rule at $E$ will give us
$\cfrac{V-V_2}{R} = \cfrac{V_2-V_3}{R} + \cfrac{V_2-V_3}{R}$
At junction $H$, we will have
$\cfrac{V_2-V_3}{R} = \cfrac{V_3-V_1}{R} + \cfrac{V_3-(V-V_2)}{R}$
At junction $D$, we will have
$\cfrac{V-V_1}{R} = \cfrac{V_1-V_3}{R} + \cfrac{V_1}{R}$
And writing the equivalent resistance equation for junction $A$ we get
$\cfrac{V}{R_{eq}} = \cfrac{V – V_2}{R} + \cfrac{V-V_1}{R} + \cfrac{V-V_1}{R}$ $\cdots$ (1)
Solving for $V_1$ and $V_2$ in terms of $V$ and substituting them in equation $1$ we get,
$R_{eq} = \cfrac{3R}{4}$
3. Cube Resistance Problem | Equivalent circuit between two adjacent vertices
Approach 1 : Equivalent circuit
Equivalent resistance between two adjacent vertices $= \cfrac{7R}{12}$. The equivalent representations are shown below which will help you understand the approach.
Note that branch 2 and 3 have horizontal symmetry (as indicated by dotted red line) which helps us simplify the circuit as shown below







After the circuit is transformed into the second figure, the total amount of resistors now becomes 13 rather than 12 as its starting in the original problem. How could that be ??? Actually there should be no any resistor between points D and F.