A molecule on the surface has greater potential energy than a molecule inside the liquid. The extra energy in the surface layer is called surface energy. Here we will examine the surface energy of a bubble and of a liquid drop of surface tension $T$ and radius $r$, followed by a review of ‘coalescing of air bubbles and radii of resulting bubble’ under isothermal conditions. Then we will determine the radius of curvature of the common surface between two bubbles, followed by the determination of change in surface energy as liquid drops coalesce together. In the end, we will look at the energy required to enlarge a bubble.
So, starting with air bubble
Surface Energy of Air Bubble
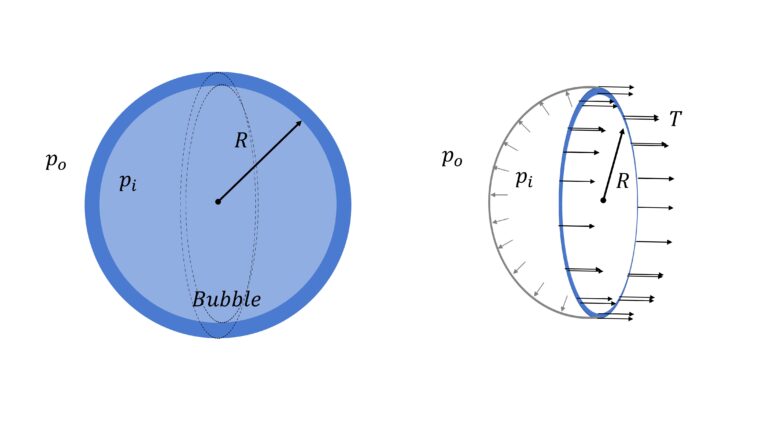
Let’s say that the pressure inside the bubble is $p_i$ and outside it, is $p_o$. So difference in pressure $\Delta p$ $=p_i – p_o$
Now, if you consider half the bubble, as shown, net force in say $x$ direction (i.e. in the horizontal direction), $F_{net, x}$ must be zero, i.e.
$F_{net,x}= \Delta p \pi R^2$ $-2 \times T \times 2 \pi R$ $=0$
or, $\Delta p = \cfrac{4T}{R}$
So, how much work will be done in increasing the radii from say $r = 0$ to $r = R$
$W = \int dW$ $= \int p dV$ $= \int_0^R \cfrac{4T}{r} 4 \pi r^2 dr$ $= 2T.4 \pi R^2$ $= T (2A)$, where $A = 4 \pi R^2$
This work done is stored as the surface energy $U$
So, $U = T.2A$
and surface energy per unit area $=\cfrac{U}{2A} = T$
Note, we have $2A$ because there are two surfaces, each of surface area ($\approx 4 \pi R^2$) in case of a bubble.
Surface Energy of Liquid Drop
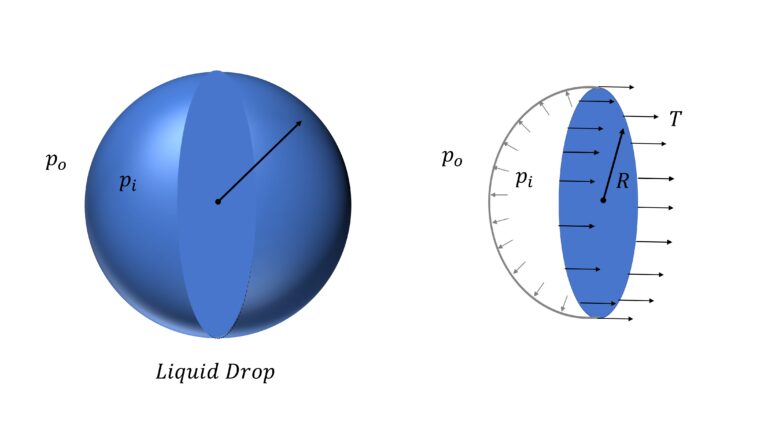
Let’s say that the pressure inside the drop is $p_i$ and outside it, is $p_o$. So difference in pressure $\Delta p$ $=p_i – p_o$
Now, if you consider half the drop,
$\Delta p \pi R^2$ $=T \times 2 \pi R$
or, $\Delta p = \cfrac{2T}{R}$
So, how much work will be done in increasing the radii from say $r = 0$ to $r = R$
$W = \int dW$ $= \int p dV$ $= \int_0^R \cfrac{2T}{r} 4 \pi r^2 dr$ $= T.4 \pi R^2$ $= T (A)$, where $A = 4 \pi R^2$
This work done is stored as the surface energy $U$,
So, $U = T.A$
and surface energy per unit surface area $=T$
Note, unlike bubble, drop has only 1 surface with area $=4 \pi R^2$.
Coalescing of Bubbles | Radii of resulting bubble
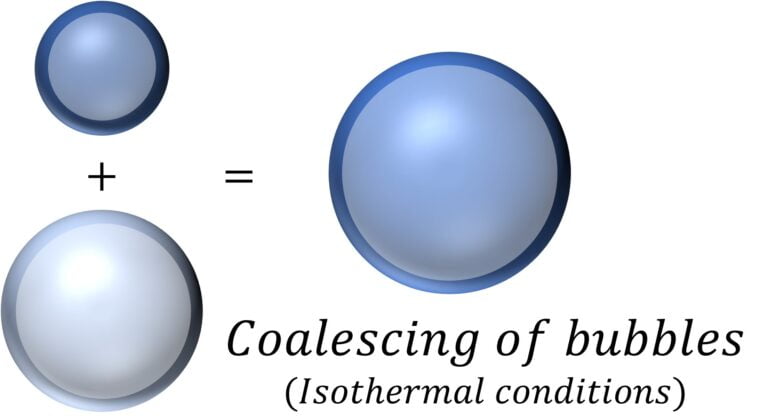
For two bubbles in vacuum, with radii $r_1$ and $r_2$, number of moles $n_1$ and $n_2$, pressure $p_1$ and $p_2$, and volume $V_1$ and $V_2$ assuming that they coalesce under isothermal conditions to form a bubble of radius $r$, number of moles $n$ ($=n_1 + n_2$), pressure $p$, and volume $V$.
Now, assuming that the gas / air in the bubbles behaves like an ideal gas, meaning the gas follows the ideal gas law: $pV = nRT$ or $\cfrac{pV}{RT} = n$
Then, it follows that $\cfrac{p_1V_1}{RT} + \cfrac{p_2V_2}{RT} = \cfrac{pV}{RT}$ [$n_1 + n_2 = n$ ]
Or, $p_1 r_1^3 + p_2 r_2^3 = p r^2$
Now, from earlier, for a bubble of radius $r$, $\Delta p = p_i – p_o = \cfrac{4T}{r}$,
In vacuum this reduces to $p_i = \cfrac{4T}{r}$
or $4T r_1^2 + 4T r_2^2 = 4T r^2$
or $r_1^2 + r_2^2 = r^2$
Radius of curvature of the common surface between two bubbles
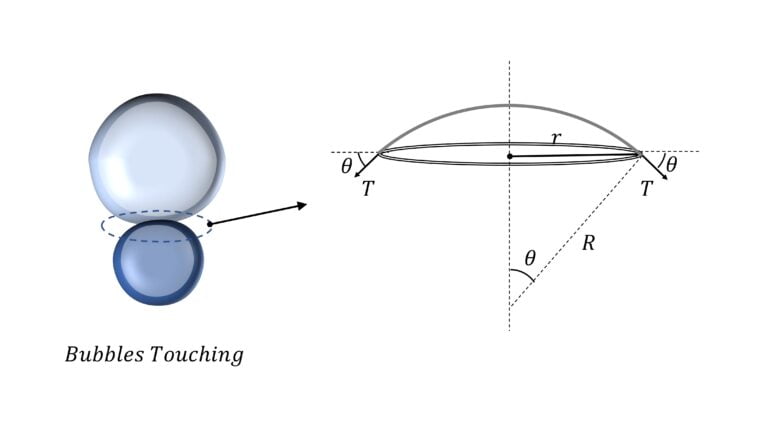
Let’s say that the pressure on the two sides of the common surface is $p_1$ and $p_2$
Then the forces on it along its axis (i.e. in the vertical direction) are:
$2T \times 2 \pi r \sin \theta$ : in the downward direction due to surface tension $T$
$|p_1 – p_2| \pi r^2$ : in the upward direction due to pressure difference
And since the net force on this surface is zero (as it is in equilibrium),
$2T \times 2 \pi r \sin \theta$ $=\Delta p \pi r^2$
or, $\Delta p = \cfrac{4T}{(r/ \sin \theta)}$ $= \cfrac{4T}{R}$
or, $R = \cfrac{4T}{\Delta p}$
Coalescing of liquid drops and resulting change in surface energy
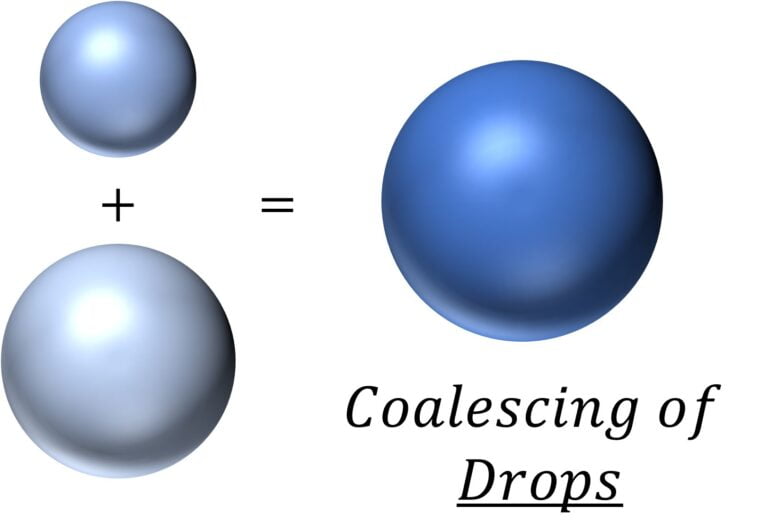
Let’s say that the two drops (of incompressible liquid) had a radius of $r_1$ and $r_2$
So, the total surface energy before coalescing is $=T.4 \pi r_1^2 + T.4 \pi r_2^2$ $=4 \pi T (r_1^2 + r_2^2)$
After coalescing together, the radius of the resulting drop is given by $V = V_1 + V_2$
i.e. $r = (r_1^3 + r_2^3)^{1/3}$
So the surface energy of the resulting drop $=4 \pi T (r_1^3 + r_2^3)^{2/3}$
Hence, drop in surface energy $=4 \pi T (r_1^2 + r_2^2 – (r_1^3 + r_2^3)^{2/3})$
This difference in energy would show up as the heat energy which will raise the temperature of the drop.
Energy required to enlarge a bubble
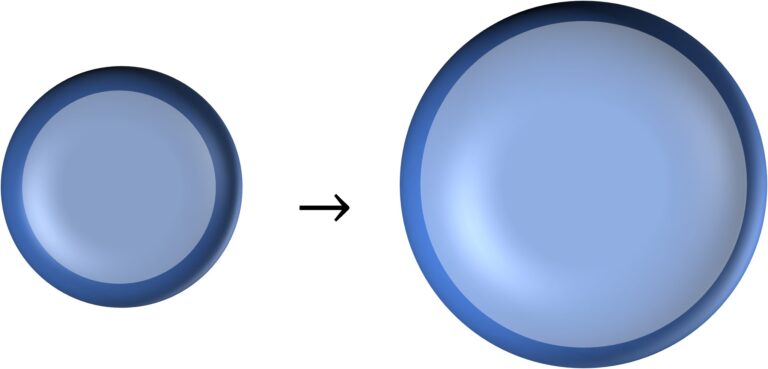
Let’s say that the initial radius of the bubble was $r_i$ and final radius is $r_f$
So, work needed $=$ increase in surface energy $=$ $2T.4 \pi (r_f^2 – r_i^2)$ $=8 \pi T (r_f^2 – r_i^2)$