From work, energy, and power you can expect one question in JEE Mains and JEE Advanced each. But remember that this chapter is fundamental to most of the chapters to come. So make sure that you develop a good comfort level with this chapter and feel free to ping us, if you have any doubts
[Note that audio solutions by Vikas Sir have been provided for all the questions under ‘Answer’ drop down]
Q1 In the spring mass system shown in the figure, the spring is compressed by $x_0 = mg/3k$ from its natural length and the block is released from rest. If initially springs are in natural length then speed of the block, when it passes through the point $P$.
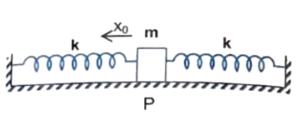
Correct answer is $g\sqrt{\cfrac{2m}{9k}}$
Q2 A single conservative force $F(x)$ acts on a $1.0 \ kg$ particle that moves along the x-axis. The potential energy $U(x)$ is given by $U(x) = 20 + (x – 2)^2$
where $x$ is in meters. At $x = 5.0 \ m$ the particle has a kinetic energy $20 \ J$.
(a) What is the mechanical energy of the system ?
(b) What is the maximum kinetic energy of the particle ?
Correct answers are
(a) $49 \ J$
(b) $29 \ J$
Q3 An object is displaced from position vector $\overrightarrow{r}_1 = (2 \hat{i} + 3 \hat{j}) \ m$ to $\overrightarrow{r}_2 = (4 \hat{i} + 6 \hat{j}) \ m$ under a force $\overrightarrow{F} = (3x^2 \hat{i} + 2y \hat{j}) \ N$. Find the work done by this force.
Correct answer is $83 \ J$
Q4 An object is acted upon by force $\overrightarrow{F}_1 = 4 \hat{i} \ N$ and $\overrightarrow{F}_2 = (\hat{i} – \hat{j}) \ N$. If the displacement of the object is $(\hat{i} + 6 \hat{j} – 6 \hat{k})$ meter, then find the change in kinetic energy of the object.
Correct answer is $ – 1 \ J$
Q5 If momentum of a body is increased by $20$ %, then find increase (in %) in kinetic energy of the body.
Correct answer is $44$
Q6 The figure shows a smooth circular path of radius $R$ in the vertical plane which subtends an angle $(\pi/2)$ at $O$. A block of mass $m$ is taken from position $A$ to $B$ under the action of a constant horizontal force $F$.
(a) Find the work done by this force.
(b) In part (a) if the block is being pulled by a force $F$ which is always tangential to the surface, find the work done by the force $F$ between $A$ and $B$.
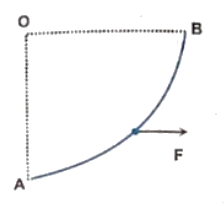
Correct answers are
(a) $FR$
(b) $\cfrac{\pi}{2}FR$
Q7 A small block of mass $m$ is kept on a rough inclined plane surface of inclination $\theta$ fixed in an elevator going up with uniform velocity $v$ and the block does not slide on the wedge. Find the work done by the force of friction on the block in time $t$.
Correct answer is $mgvt \sin^2 \theta$
Q8 A particle moves from a point $\overrightarrow{r}_1 = (2 \hat{i} + 3 \hat{j})$ to another point $\overrightarrow{r}_2 = (3 \hat{i} + 2 \hat{j})$ during which a certain force $\overrightarrow{F} = (5 \hat{i} + 5 \hat{j})$ act on it. Calculate work done by the force on the particle during this displacement.
Correct answer is zero.
Q9 A force $F = a + bx$ acts on a particle in the $x$ direction, where $a$ and $b$ are constants. Find the work done by this force during a displacement from $x =0$ to $x = d$
Correct answer is $(a + bd/2)d$.
Q10 A small body is projected up a rough $\left(\mu = \cfrac{1}{2}\right)$ inclined plane $(\theta = 60^{\circ})$ with a speed of $v = 10 \ m/s$ as shown. How far along the plane it moves up before coming to rest ?
(Take $g = 10 \ m/s^2$)
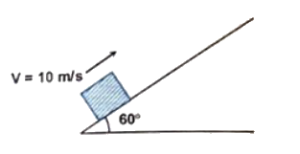
Correct answer is $\cfrac{20}{2\sqrt{3} + 1} \ m$.
Q11 A block of mass $m$ is attached to two un-stretched springs of spring constants $k_1$ and $k_2$ as shown in figure. The block is displaced towards right through a distance $’x’$ and is released. Find the speed of the block as it passes through a distance $x/4$ from its mean position.
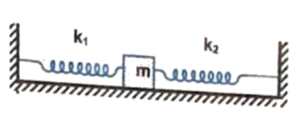
Correct answer is $\cfrac{x}{4}sqrt{\cfrac{15(k_1 + k_2)}{m}}$.
Q12 An observer and a vehicle, both start moving together from rest with accelerations $5 \ m/s^2$ and $2 \ m/s^2$, respectively. There is a $2 \ kg$ on the floor of the vehicle, and $\mu = 0.3$ between their surfaces. Find the work done by frictional force on the $2 \ kg$ block as observed by the running observer, during first $2$ seconds of the motion.
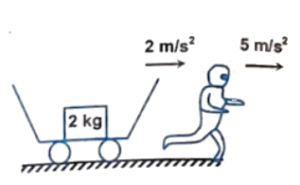
Correct answer is $ – 24$ Joule.
Q13 In the above problem, if the observer and vehicle start moving in opposite directions, from rest, then find the direction and magnitude of frictional force acting between the surface of the block and floor of vehicle, as seen by the observer. Also, calculate the work done by the frictional force during first $2$ seconds of motion.
Correct answer are
(a) $4 \ N$ along movement of vehicle,
(b) $56$ Joule
Q14 A stone with weight $W$ is thrown vertically upwards into the air with initial speed $v_0$. If a constant force $f$ due to air drag acts on the stone throughout its flight,
(a) Show that the maximum height reached by the stone is $h = \cfrac{v_0^2}{2g[1 + (f/W)]}$
(b) Show that the speed of the stone upon impact with the ground is $v = v_0\left(\cfrac{W – f}{W + f}\right)^{1/2}$
Let’s see how you should approach this question.
Q15 A $16 \ kg$ block moving on a frictionless horizontal surface with a velocity of $4 \ m/sec$ compresses an ideal spring and comes to rest, momentarily, If the force constant of the spring be $100 \ N/m$, then how much is the spring compressed ?
Correct answer is $1.6 \ m$
Q17 One end of a spring of natural length $h$ and spring constant $k$ is fixed at the ground and the other is fitted with a smooth ring of mass $m$ which is allowed to slide on a horizontal rod fixed at height $h$ as shown in the figure. Initially, the spring makes an angle of $37^{\circ}$ with the vertical when the system is released from rest. Find the speed of the ring when the spring becomes vertical.
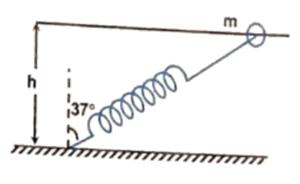
Correct answer is $\cfrac{h}{4}\sqrt{\cfrac{k}{m}}$
Q18 An automobile of mass $’m’$ accelerates starting from rest, while the engine supplies constant power $P$. Show that:
(a) the velocity is given as a function of time by $v = (2Pt/m)^{1/2}$
(b) the position is given as a function of time by $s = (8P/9m)^{1/2}t^{3/2}$
….
Q19 A particle is hanging from a fixed point $O$ by means of a string of length $’a’$. There is a small nail $’Q’$ in the same horizontal line with $O$ at a distance $b (b = a/3)$ from $O$. Find the minimum velocity with which the particle should be projected so that it may make a complete revolution around the nail without being slackened.
Correct answer is $2\sqrt{ga}$
Q20 A rod of mass $m$ and length $l$ is kept on a smooth wedge of mass $M$ as shown in the figure. If the system is released when the rod is at the top of the wedge, find the speed of the wedge when the rod hits the ground level. [Neglect friction between all surfaces in contact.]
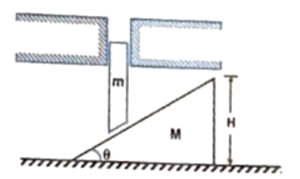
Correct answer is $\sqrt{\cfrac{2mgH}{M + m \tan^2 \theta}}$





It was very useful to me,