From rotation, you can expect 1 to 2 questions in JEE Main and 1 to 2 questions in JEE Advanced & it is considered one of the more difficult topics in physics.
Q1 A sphere of mass $m$ and radius $R$ rests on sufficiently rough inclined plane in equilibrium as shown in the figure. Find the tension in the string.
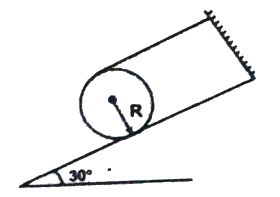
Correct answer is $mg/4$
Q2 A $T$-shaped object with dimensions shown in the figure. is lying on a smooth floor. A force $\overrightarrow{F}$ is applied at the point $P$ parallel to $AB$, such that the object has only the translational motion without rotation. Find the location of $P$ with respect to $C$.
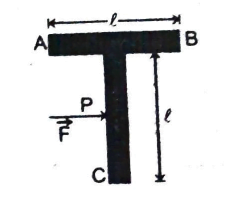
Correct answer is $3l/4$
Q3 A bead of mass $m$ slides on a hemispherical surface with a velocity $v$ at an angular position $\theta$. If the coefficient of friction between the bead and hemispherical ‘surface ig $\mu$, Find the magnitude of Angular momentum of the bead about $O$ in the position shown.
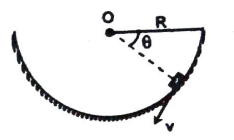
Correct answer is $mvR$
Q4 A solid ball of mass $m$ and radius $R$ is given linear velocity $V$ and no angular velocity and placed on a rough surface. What is the velocity of center of mass when ball starts pure rolling.
Correct answer is $5v/7$
Q5 A time varying force $F = 2t$ is applied on a spool as shown in the figure. The angular momentum of the spool at time $t$ about bottommost point is :
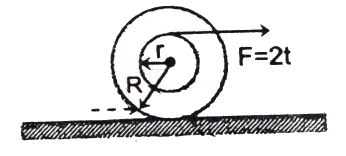
Correct answer is $(R + r)t^2$
Q6 A solid cylinder of mass $m$ is suspended through two strings wrapped around it as shown in figure. If the cylinder is released from rest, then find:
(a) the tension $T$ in the string, and
(b) the speed of the cylinder as it falls through a distance $h$.
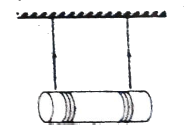
Correct answers are
(a) $\cfrac{mg}{6}$
(b) $\sqrt{\cfrac{4gh}{3}}$
Q7 A disc of radius $R$ is rolling on a straight surface $S$ without slipping (velocity of the point of contact $P$ relative to $S = 0$). The instantaneous angular velocity $\omega$ and angular acceleration $\alpha$ are as shown in the figure. Find
(a) the velocity and acceleration of point $O, \ A$ and $P$ on the disc relative to the surface $S$.
(b) the velocity and acceleration of point $A$ relative to point $B$.
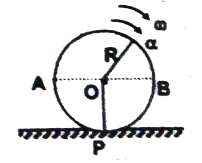
Correct answers are
(a) $\quad \overrightarrow{V_{OS}} = \omega R \hat{i} \qquad \qquad \overrightarrow{a_{OS}} = \alpha R \hat{i}$
$\qquad \overrightarrow{V_{AS}} = \omega R (\hat{i} + \hat{j}) \qquad \qquad \overrightarrow{a_{AS}} = (\alpha + \omega^2) R \hat{i} + \alpha R \hat{j}$
$\qquad \overrightarrow{V_{PS}} = 0 \qquad \qquad \overrightarrow{a_{PS}} = \omega^2 R \hat{j}$
(b) $\quad \overrightarrow{V_{AB}} = 2 \omega R \hat{j} \qquad \qquad \overrightarrow{a_{AB}} = 2R (\omega^2 \hat{i} + \alpha \hat{j})$
Q8 A uniform rod of mass $m$ and length $L$ is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod is released from rest in the position shown by slightly displacing it clockwise. Find the hinge reaction at the axis of rotation at the instant the rod turns through (a) $90^{\circ}$ and (b) $180^{\circ}$.
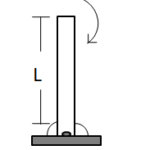
Correct answers are
(a) Horizontal component $ = \cfrac{3mg}{2} \ \leftarrow$, Vertical component $ = \cfrac{mg}{4} \ \uparrow$
(b) Horizontal component $ = $zero, Vertical component $ = 4mg \ \uparrow$.
Q9 A uniform sphere of radius $r$ starts rolling down without slipping from the top of another fixed sphere of radius $R$ shown in the figure. Find the angular velocity of sphere of radius $r$ at the instant when it leaves contact with the surface of the fixed sphere.
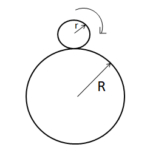
Correct answer is $\sqrt{\cfrac{10 g (R + r)}{17 r^2}}$
Q10 A rotating ball hits a rough horizontal plane with a vertical velocity $v$ and angular velocity $\omega$. Given that the coefficient of friction is $\mu$ and the vertical component of the velocity after the collision is $v/2$. find (a) the angular velocity after the collision (h) the impulsive ground reaction during the collision.
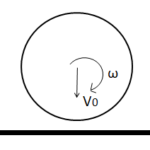
Correct answers are
(a) $\omega – \cfrac{15 v \mu}{4R}$
(b) $\cfrac{3mv}{2}\sqrt{1 + \mu^2}$
Q11 In case of purely rolling body, static friction is usually needed to cause the body to roll without slipping, But as friction is a dissipative force, how can we justify the use of law of conservation of mechanical energy ?
Correct answer is, Friction is acting at the point of contact but the point of contact always remains stationary relative to the surface and hence work done by the frictional force on the body is zero. Hence we can use the conservation of mechanical energy.
Q12 A uniform circular disc of mass $m$ and radius $R$ is rolling on a horizontal surface. Find the angular momentum of the disc about an axis perpendicular to the plane of disc and fixed at point $P$ to the disc.
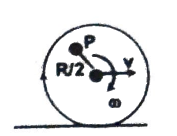
Correct answer is $\cfrac{3}{4} m R^2 \omega$
Q13 A cord is wrapped around the rim Of a flywheel $0.5 \ m$ in radius and a steady pull of $50 \ N$ is applied on the cord as shown in the figure. The wheel is mounted on a frictionless bearing on the horizontal shaft through its center. The moment of inertia of the wheel is $4 \ kg \ m^2$. (about center of wheel)
(a) Compute angular acceleration of the wheel.
(b) If a mass having a weight $50 \ N$ hangs from the cord as shown in the figure, compute the angular acceleration of the wheel. Why is this not the same as in part (a) ? (take $g = 10 m/s^2$)
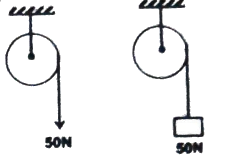
Correct answers are
(a) $6.25 \ rad/s^2$
(b) $4.76 \ rad/s^2$ (in the first case the tension in the string is $50 \ N$ while in the latter case it is lesser)
Q14 A uniform rod of length $L$ and mass $2M$ rests over two supports $A$ and $B$. A particle having mass, $M$ is placed at the right end. Find the reactions at supports $A$ and $B$.
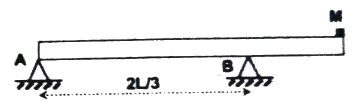
Correct answer is $N_A = 0, \ N_B = 3Mg$
Q15 A uniform ring of mass $m$ and radius $R$ has a particle of mass $2m$ rigidly attached to it on the inside surface. The system rolls on a horizontal surface without slipping. In the position shown at a certain instant, its center $C$ has a velocity $v_0$. Find the kinetic energy of the system.
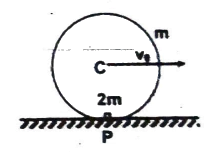
Correct answer is $mv_0^2$
Q16 A solid sphere of mass $m$ and radius $R$ is placed on a plank of equal mass. which lies on a smooth horizontal surface. The sphere is given a sharp impulse in the horizontal direction so that it starts sliding with a speed of $v_0$. Find the time taken by the sphere to start pure rolling on the plank. The coefficient of friction between plank and sphere is $\mu$.
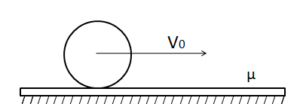
Correct answer is $2v_0/9 \mu g$
Q17 Two thin planks are moving on a four identical cylinder as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder
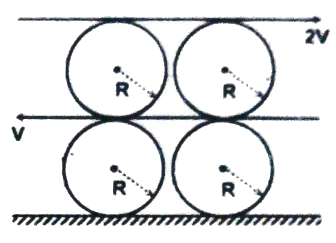
Correct answer is $3$
Q18 A rod of length $l$ is standing vertically frictionless surface. It is disturbed slightly from this position Let $\omega$ and $\alpha$ be the angular speed and angular acceleration of the rod, when the rod turns through an angle $\theta$ with the vertical, then find the value of acceleration of center of mass of the rod .
Correct answer is $\cfrac{l \alpha}{2} \sin \theta + \cfrac{\omega^2 l}{2} \cos \theta$
Q19 Three identical cylinders of radius $R$ are in contact. Each cylinder is rotating with angular velocity $\omega$. A thin belt is moving without sliding on the cylinders. Calculate the magnitude of velocity of point $P$ with respect to $Q$. $P$ and $Q$ are two points of belt which are in contact with the cylinder.
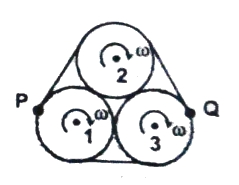
Correct answer is $R \omega\sqrt{3}$
Q20 A rod of mass $m$ and length $2R$ can rotate about an axis passing through $O$ in vertical plane. A disc of mass $m$ and radius $R$ is hinged to the other end $P$ of the rod and can freely rotate about $P$. When disc is at lowest point both rod and disc has angular velocity $\omega$. If rod rotates by maximum angle $\theta = 60^{\circ}$ with downward vertical, then find $\omega$ in terms of $R$ and $g$. (all hinges are smooth)
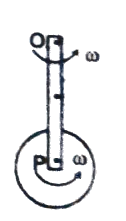
Correct answer is $\sqrt{\cfrac{9g}{16R}}$
Q21 A uniform disc of surface mass density $(\sigma)$ exists in space. Its radius is $R$. A small disc of radius $(R/2)$ is cut from it as shown in the figure. The moment of inertia (I) about axis $AB$ is $\cfrac{15}{16K} \sigma \pi R^4$. Find the value $K$.
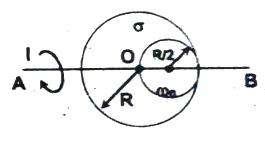
Correct answer is $4$
Q22 A sphere of mass $m$ and radius $R$ rolls without sliding on a horizontal surface. It collides with a light spring of stiffness $K$ with a kinetic energy $E$. If the surface $(AB)$ under the spring is smooth and $E = 7 \ J$ and $K = 10 \ N/m$, find the maximum compression of the spring.
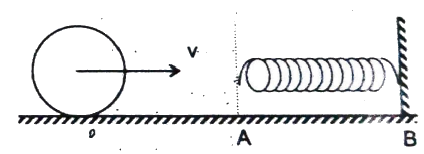
Correct answer is $1$
Q23 A semi-circular disc of radius $1 \ m$ and mass $= 4 \ kg$ is lying on the horizontal $x$-$y$ plane. If $XX’$ is the axis of rotation of the body and a force $= 2N \ \hat{k}$ is applied at point $P$, find the magnitude of angular acceleration (the region is gravity free) (in $rad/s^2$).
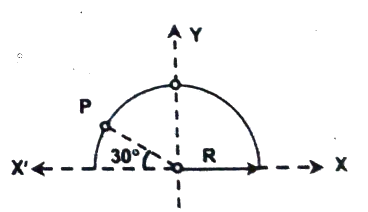
Correct answer is $1$
Q24 A uniform rod $AB$ of mass $m$ and length $l$ is at rest on a smooth horizontal surface. A horizontal impulse $P$ is applied to the end $B$ perpendicular to the rod. The time taken by the rod to turn through a right angle is $\cfrac{\pi K m l}{12P}$. Find the value of $K$.
Correct answer is $1$