Welcome to the first of the two podcasts on Newton’s Laws of Motion, where in we will start the discussion with a brief overview of 3 laws of motion before diving into newton’s 2nd law F=dp/dt or F ma and understand how to apply this seemingly simple equation to different scenarios and, either, determine the acceleration of the involved masses, given the forces acting on them, or, determine the unknown force given the acceleration of involved masses

And before we get started, I would mention that learning to apply newton’s 2nd law to different scenarios is a skill that needs to be developed through practice, just like any other skill and there are no shortcuts to it if you want to become really good at it. And good thing is that, if you are persistent, this skill will grow rapidly and will surprise you.

With that let’s revisit the 3 laws of motion.

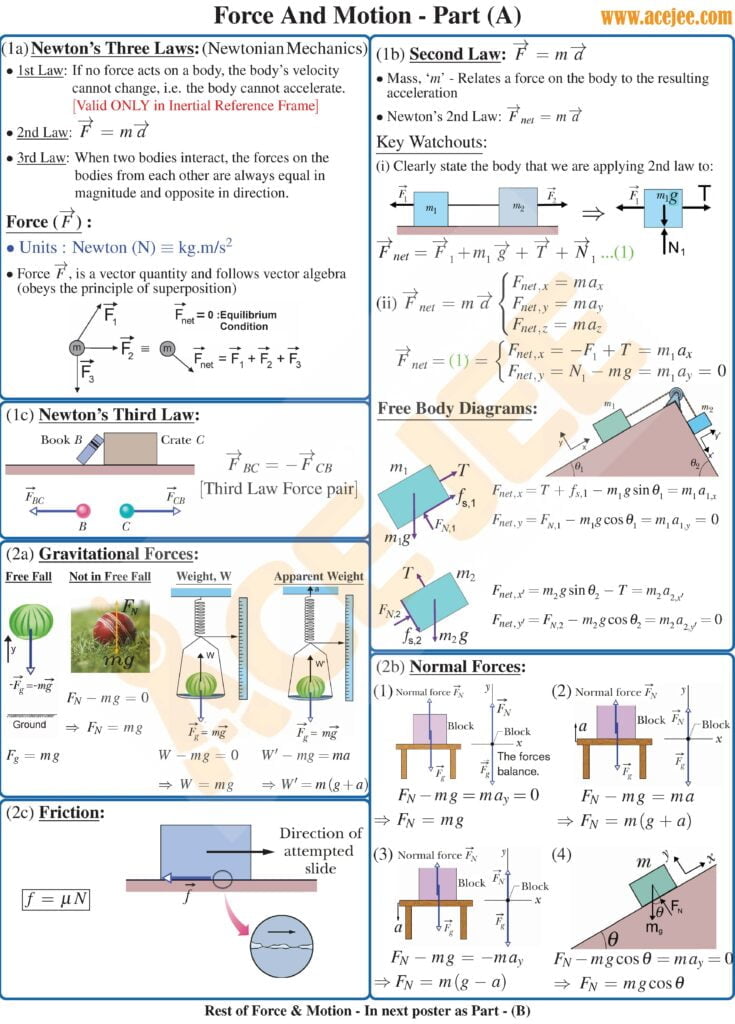
So, newton’s first law states that a body at rest will tend to remain at rest, unless a net external force acts on the body resulting in its acceleration and what do we mean by net external force, well, there might be two or more forces acting on a body but if they cancel each out, meaning, there is no net external force and as such the body will not move.

Ok, now, what if the body is not at rest but rather is moving. What does Newton’s 1st law say about it. Well it says that the body will continue to move at uniform velocity unless a net external force acts on it and result in acceleration, thus changing its velocity.

This leads us to the 2nd law of motion, which states that, when a net force acts on a particle, it results in its acceleration which is directly proportional to the net external force acting on the particle and inversely proportional to the mass of the particle, i.e. a = F/m or we can say F is equal to mass times acceleration. Alternate form of F = ma is F = dP/dt or rate of change of momentum. Note that P or linear momentum of a particle is defined as product of its mass and its velocity and is a vector quantity. So it we differentiate momentum P with respect to time, we will get m times dv/dt or m times a. In other words F = ma and F = dp/dt are different forms of the same equation. 

Now before we move any further, note that F = ma is a vector equation as net force F and acceleration ‘a’, both are vectors and as per this equation, the two should be in the same direction. Moreover since net force vector F is equal to ma vector, their x, y and z components must also be equal, which then gives us 3 scalar equations Fx = ma_x, Fy = ma_y and Fz = ma_z. So what they imply is that x component of force vector F is equal to mass times the x component of acceleration vector, y component of the force vector F is equal to mass times the y component of acceleration vector and similarly, z component of force vector F is equal to mass times the z component of acceleration vector.

Ok, Now this newton’s 2nd law, which is defined for a particle, seems simple enough but how we apply it to different situations to understand the motion of masses connected to each other requires good amount of practice. More you practice, more skilled you will get in its application, just like learning any new skill. But the key is to be able to look at each of these connected particles separately, identify all the different forces that are acting on the particle at hand, find the component of resultant vectors along x, y and z and then write newton’s 2nd law to find the acceleration of that particle in x, y and z directions. The following steps involves establishing how the accelerations of different particles connected together are related and you will end up with multiple equations, wherein, the number of unknowns would typically match the number of equations and you should then be able to solve for the unknowns

Note that the diagrams we draw, for each individual particle to examine the forces acting on it are called free body diagrams

And before we talk about these free body diagrams and commonly encountered forces when drawing such diagrams, let’s briefly talk about Newton’s 3rd law as this will come in handy when drawing free body diagrams.

So, newton’s third law simply states that, when two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction

With that let’s dig into free body diagrams and we will start with gravitational force that earth exerts on the masses or particles, followed by normal force, which two particles that are pressing against each other apply on each other perpendicular to the contact surface, followed by frictional force that two rough surfaces in contact with each other exert on each other along the surface with these forces acting so as to prevent the relative motion of the two surfaces.

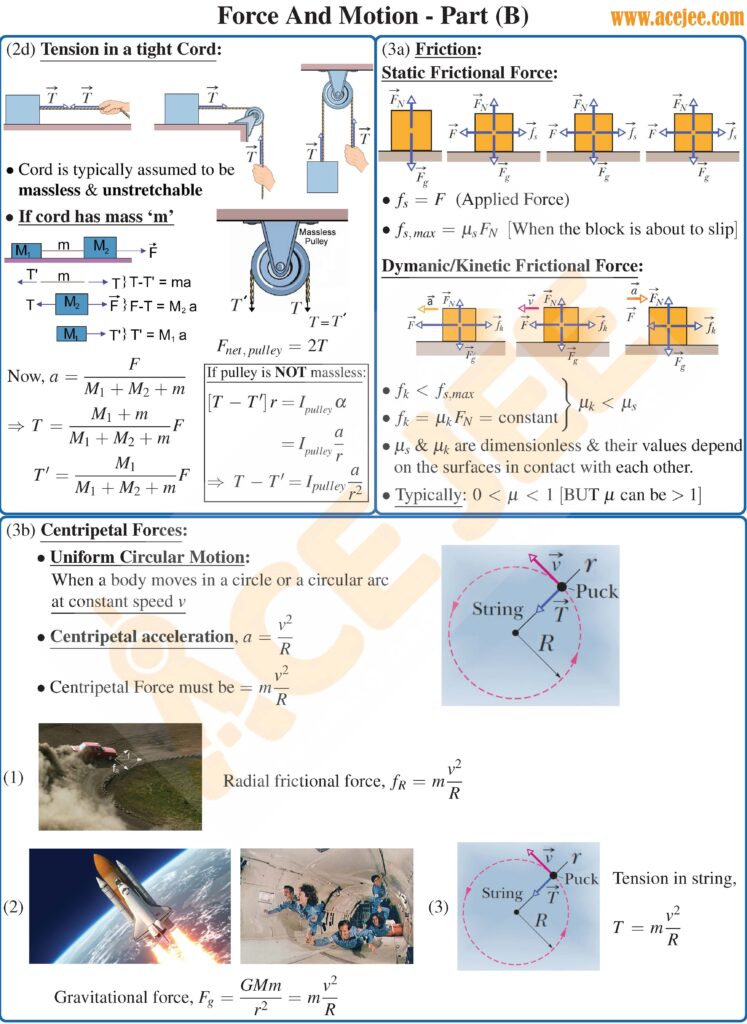
In the following podcast, we will talk about tension in cord or string and further examine frictional forces for two scenarios. One in which there is tendency to slide but the surfaces are not moving relative to each other and second in which surfaces are sliding past each other.

 Additionally in that podcast we will talk about centripetal or center seeking forces and also touch upon centrifugal forces.

So starting with gravitational force on the particle, this force is directed towards the center of earth or we can say perpendicular to the ground and pointed downwards and is simply equal to mass times gravitational acceleration $g$, which is the acceleration the particle would have if allowed to fall freely.

Moving to normal forces between two surfaces in contact, normal force exerted on one body or surface, due to other, is perpendicular to the contact surface and pointed as if it is pushing the body away from the other body and its magnitude adjusts itself automatically to ensure that there is no net force on the body, perpendicular to the surface and pointed towards the other body as that would imply that the bodies will breach their surfaces and drive into each other, something that rigid bodies do not allow.

And once again normal force is perpendicular to the contact surface. And to test your understanding, think about a ladder leaning against a rigid wall. What will be the direction of the normal force and as you might have guessed it will be perpendicular to the wall

Now, think about a tall ladder that is placed against a short wall such that part of the ladder extends beyond the wall. What will be the direction of the normal force. Well as you might have guessed, it will be perpendicular to the ladder.

In case you are wondering why, the normal force is perpendicular to wall in one case and perpendicular to ladder in other, carefully examine the contact surface of the short ladder in the 1st case and contact surface of short wall in 2nd case and yes remember that the edge has some radius of curvature, no matter how small. If still in doubt, reach out to us.

With that let’s talk about frictional force.

So to begin with, as you have been studying in your earlier classes or grades, frictional force acts to oppose the sliding of surfaces past each other and what’s behind this force. Well, at the microscopic level, the surfaces are not smooth rather they look like a mountain range with peak and valleys. So when the two surfaces come into contact, in reality, the actual contact area is very small meaning that the pressure at this contact points is significant and as a result the contact points weld together. So when we try to move or slide the two surfaces past each other, we need to break these welded sections and also break or shear peaks of the two surfaces which is what the frictional force is and it is directly proportional to the normal force between the two surfaces and the proportionality constant is called or referred to as the coefficient of friction.

Now before we conclude this podcast let’s talk about few scenarios where in relative motion of rigid bodies is different from the relative motion between their contact surfaces. For example, when we see a person walking along say an incline, the frictional force is in the forward direction i.e. direction of the motion and is what is allowing the person to walk . This may seem confusing at first because we see person moving in the forward direction and intuitively assume that the frictional force will oppose this forward motion relative to ground and hence act in the backward direction, but if you look closely at their feet, the foot is trying to slide backwards relative to the ground and as a result the frictional force is in the forward direction. If that didn’t make sense, think about it and you will get it

Now let’s talk about motion of a bicycle. Can you guess the direction in which the frictional force is acting on the rear and front wheel as the cyclist is accelerating in the forward direction. Well, let’s examine them separately.

As for the rear wheel as the cyclist is trying is pressing on the pedals, the pedals exert torque on the rear wheel and try and spin it faster. As a result the bottom part of the wheel in contact with the ground is tending to slide in the backward direction relative to the ground and as a result the frictional force will act in the forward direction on the rear wheel

Now let’s talk about the front wheel. So, as the frictional force acts in the forward direction on the rear wheel it tries to accelerate the bicycle in the forward direction and as a result the frame of the cycle which is connected to the center of the front wheel accelerates the front wheel in the forward direction and as a result the contact surface of the front wheel with the ground will tend to slide in the forward direction and as a result the frictional force on the front wheel will be in the backward direction.

And that concludes this podcast and we will cover the remaining concepts and a brief overview of types of questions in the 2nd podcast on force and motion.