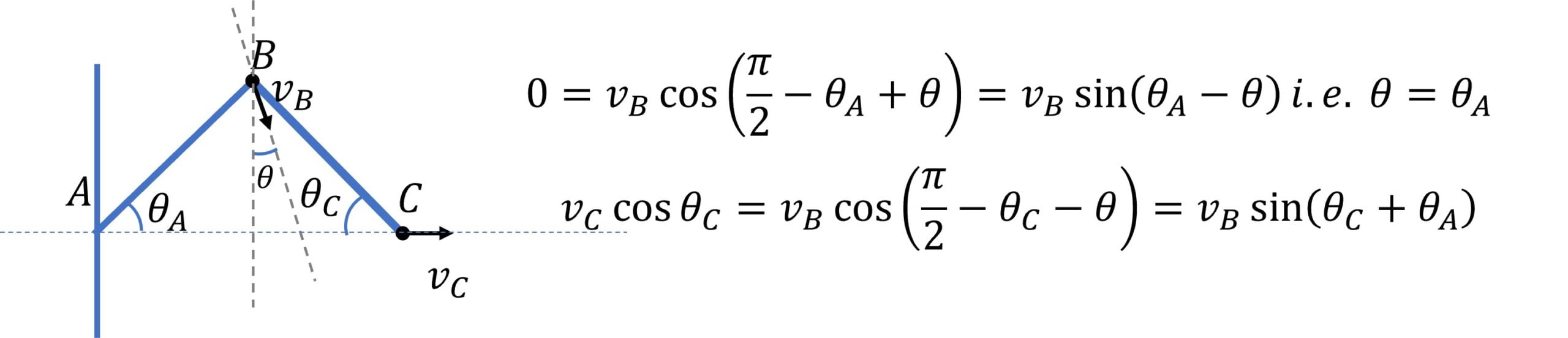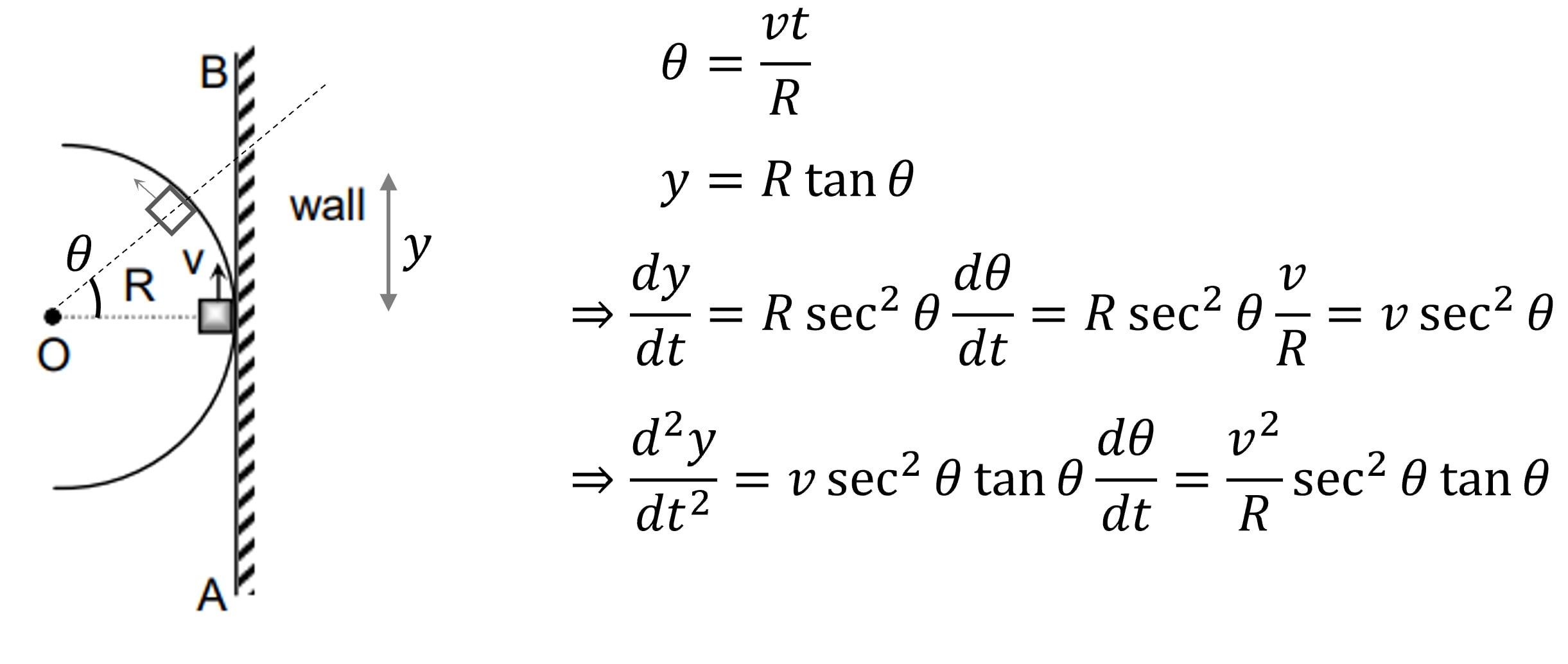In this blog, you will learn to establish the relationship between the motion of rigid bodies that are constrained to move together in some direction or establish a relation between the motion of different points of a rigid body.
And to help you become successful, let’s look at some fundamentals that will be of help as you try and solve 20 or so advanced level questions in this blog.
Question 1 (Only one correct answer)
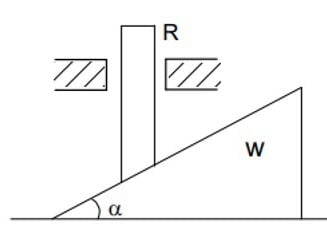
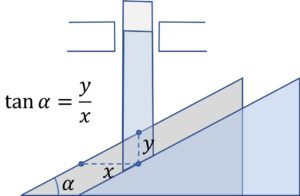
In the arrangement shown, all surfaces are frictionless. The rod R is constrained to move vertically. The vertical acceleration of $R$ is $a_1$ and the horizontal acceleration of the wedge $w$ is $a_2$. The ratio $\cfrac{a_1}{a_2}$ is equal to
A) $\tan \alpha$
B) $\cot \alpha$
C) $\sin \alpha$
D) $\cos \alpha$
Question 2 (Numerical Answer)
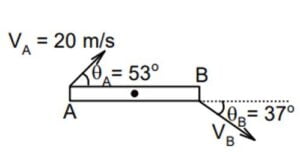
The two ends $A$ and $B$ of a uniform rod of length $l=1 \ m$ are moving with velocities $V_A$ and $V_B$ as shown. The velocity $V_B$ (m/s) is
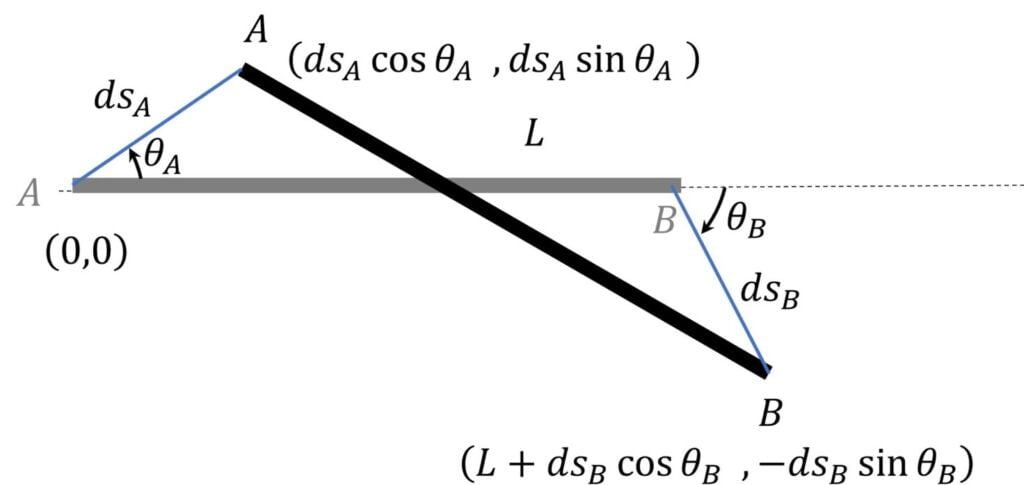
As the points $A$ and $B$ move to new points (marked in bold) after a small (or differential) time $dt$, new $x$ and $y$ coordinates are as shown in the figure.
Now, the distance between new coordinates of $A$ and $B$ should still be $L$, as the rod is not expanding or contracting in length
i.e. $(L + ds_B \cos \theta_B – ds_A \cos \theta_A)^2$ $+ (ds_B \sin \theta_B + ds_A \sin \theta_A)^2$ $= L^2$
Now, ignoring the 2nd order terms, we will get
$ds_B \cos \theta_B – ds_A \cos \theta_A = 0$
or $\cfrac{ds_B}{dt} \cos \theta_B = \cfrac{ds_A}{dt} \cos \theta_A$
or $v_B \cos \theta_B = v_A \cos \theta_A$
Correct answer is (15)
Question 3 (Only one correct answer)
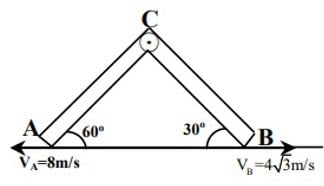
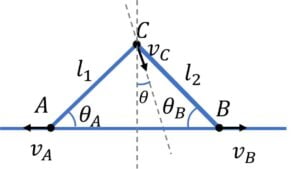
Two rods $AC$ and $BC$ are hinged at the end ‘$C$’and the ends $A$ and $B$ are moving along the surface with velocities $V_A = 8 \ m/s$ and $V_B = 4 \sqrt{3} \ m/s$ respectively as shown. The velocity of hinged point ‘$C$’ is
(A) $\sqrt{13} m/s$
(B) $2\sqrt{13} m/s$
(C) $3\sqrt{13} m/s$
(D) $4\sqrt{13} m/s$
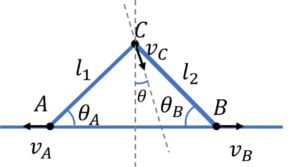
Let’s say that joint $C$ is moving with speed $v_C$ at an angle $\theta$ from the vertical as shown,
then using the fact that for a rod, the component of velocities of the two ends along the rod should be the same (as rod is not expanding or contracting in length) we get,
For rod AC:
$v_A \cos \theta_A = v_C \cos \left( \cfrac{\pi}{2} – \theta_A + \theta \right)$ $= v_C \sin (\theta_A – \theta)$
For rod BC:
$v_B \cos \theta_B = v_C \cos \left( \cfrac{\pi}{2} – \theta_B – \theta \right)$ $= v_C \sin (\theta_B + \theta)$
From these two equations, we should be able to solve for the unknown.
Correct answer is (B)
Question 4 (Only one correct answer)
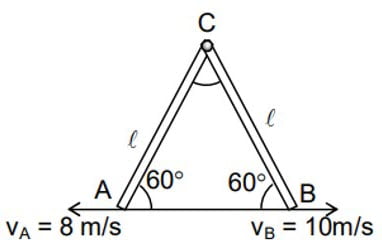
Two rods of equal length $AC$ and $BC$ are freely joined at $C$. Two ends $A$ and $B$ are pulled with velocities $8$ m/s and $10$ m/s as shown in the figure, at a particular instant. The velocity of the point $C$ at this instant is
(A) $2 \sqrt{7}$ m/s
(B) $3 \sqrt{7}$ m/s
(C) $4 \sqrt{7}$ m/s
(D) $6 \sqrt{7}$ m/s
As the points $A$ and $B$ move to new points (marked in bold) after a small (or differential) time $dt$, new $x$ and $y$ coordinates are as shown in the figure.
Now, the distance between new coordinates of $A$ and $B$ should still be $L$, as the rod is not expanding or contracting in length
i.e. $(L + ds_B \cos \theta_B – ds_A \cos \theta_A)^2$ $+ (ds_B \sin \theta_B + ds_A \sin \theta_A)^2$ $= L^2$
Now, ignoring the 2nd order terms, we will get
$ds_B \cos \theta_B – ds_A \cos \theta_A = 0$
or $\cfrac{ds_B}{dt} \cos \theta_B = \cfrac{ds_A}{dt} \cos \theta_A$
or $v_B \cos \theta_B = v_A \cos \theta_A$
Correct answer is (A)
Question 5 (Only one correct answer)
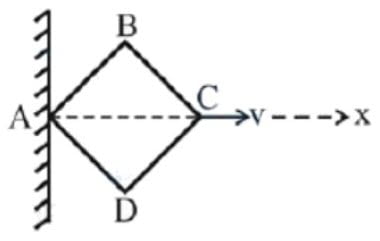
Four rods each of length $l$ have been hinged to form a rhombus. Vertex $A$ is fixed to rigid support, vertex $C$ is being moved along the $x-$ axis with a constant velocity $v$ as shown in the figure. The rate at which vertex $B$ is approaching the $x-$ axis at the moment the rhombus is in the form of a square is
Question 6
Consider the following diagram in which an inextensible string connects two blocks passing via ring. The first block moves with a velocity of $2 \ ms^{-1}$ and the second one moves with a velocity of $v \ ms^{-1}$. If the ring slides on horizontal rod then the value of $v$ is (in $ms^{-1}$)
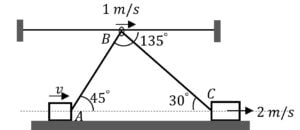
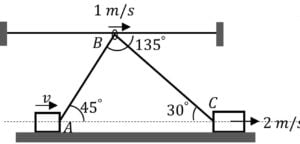
Here note that string AB will get shorter in size while string BC will get longer and since the length of the string A-B-C is constant. It will then imply that the rate of shorterning of AB should be equal to rate at which BC is increasing in length
Now, rate at which length AB is reducing is $= v_A \cos 45^{\circ}$ $+ v_B \cos 135^{\circ}$
& rate at which length BC is increasing is $= v_C \cos 30^{\circ}$ $- v_B \cos 30^{\circ}$
So, $v_A \cos 45^{\circ}$ $+ v_B \cos 135^{\circ}$ $=v_C \cos 30^{\circ}$ $- v_B \cos 30^{\circ}$
Correct answer is ($\sqrt{\cfrac{3}{2}} + 1$)
Question 7 (Only one correct answer)
Point $A$ on the rod $AB$ has an acceleration of $5 \ m/s^2$ and a velocity of $6 \ m/s$ at an instant as shown in the figure. The acceleration of the end $B$ at the same moment is:
(A) $- \cfrac{80}{3} \hat{i} \ m/s^2$
(B) $\cfrac{80}{3} \hat{i} \ m/s^2$
(C) $- \cfrac{40}{3} \hat{i} \ m/s^2$
(D) $- \cfrac{75}{6} \hat{i} \ m/s^2$
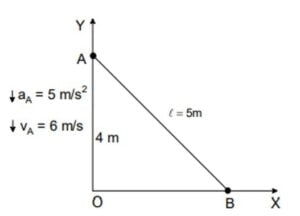
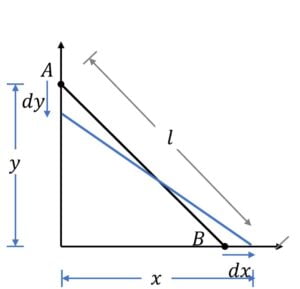
To relate $v_A$ & $v_B$ and $a_A$ & $a_B$, we can take one of the two approaches
Approach 1 (using the coordinate geometry)
Let’s say that at some time $t$, $A$ is at ($0,y$) and $B$ is at ($x,0$) and let’s say that after a small or differential amount of time $dt$, $A$ descends by a distance $-dy$, and in the same time, $B$ moves to the right by $dx$
so new coordinates of $A$ and $B$ are ($0,y+dy$) and ($x+dx,0$) respectively
Now, since the length of the rod must remain $L$ at all times,
$(x+dx)^2 + (y+dy)^2 = L^2$
Now, ignoring the 2nd order differential terms, we get
$2x dx + 2ydy = 0$ (note $x^2 +y^2 = L^2$)
Now dividing both sides by differential time ‘$dt$’, we get
$2 x \cfrac{dx}{dt} + 2 y \cfrac{dy}{dt} = 0$
We could have obtained the same relationship by simply differentiating $x^2 + y^2 = L^2$ with respect to time $t$.
i.e. $x v_B – y v_A = 0$ (Note v_A = – \cfrac{dy}{dt})
Now differentiating this equation with time $t$ once more we will get
$v_B^2 + x a_B + v_A^2 – y a_A = 0$
Approach 2 (using the derived relation that speed of $A$ and $B$ along the rod should be the same)
$v_A \cos \theta = v_B \sin \theta$, where $\theta$ is the angle that the rod makes with the vertical
Now $\cos \theta = \cfrac{y}{L}$ and
$\sin \theta = \cfrac{x}{L}$
i.e. $x v_B – y v_A = 0$
Rest of the steps are same as in Approach 1
Correct answer is (A)
Question 8 (Integer Answer)
Question 9 (Only one correct answer)
(i) The angular velocity of rod is:
(A) $\sqrt{3}$ rad/sec
(B) $\sqrt{5}$ rad/sec
(C) $\sqrt{\cfrac{5}{3}}$ rad/sec
(D) $\sqrt{\cfrac{3}{5}}$ rad/sec
(ii) The velocity of center of mass of rod is
(A) $\sqrt{5}$ m/s
(B) $\sqrt{10}$ m/s
(C) $\sqrt{15}$ m/s
(D) $\sqrt{20}$ m/s
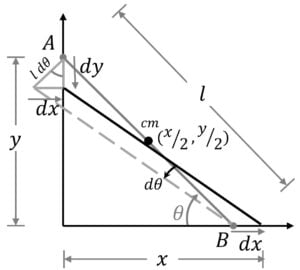
Coordinates of center of mass (cm) at any point in time can be written in terms of the coordinates of $A$ ($0,y$) and $B$ ($x,0$) as $(\cfrac{x}{2}, \cfrac{y}{2})$
i.e. $\overrightarrow{r}_{cm} = \cfrac{x}{2} \hat{i} + \cfrac{y}{2} \hat{j}$
Differentiating it with respect to time $t$, we get
$\overrightarrow{v}_{cm} = \cfrac{1}{2} \cfrac{dx}{dt} \hat{i} + \cfrac{1}{2} \cfrac{dy}{dt} \hat{j}$
i.e. $\overrightarrow{v}_{cm} = \cfrac{1}{2} v_B \hat{i} – \cfrac{1}{2} v_A \hat{j}$
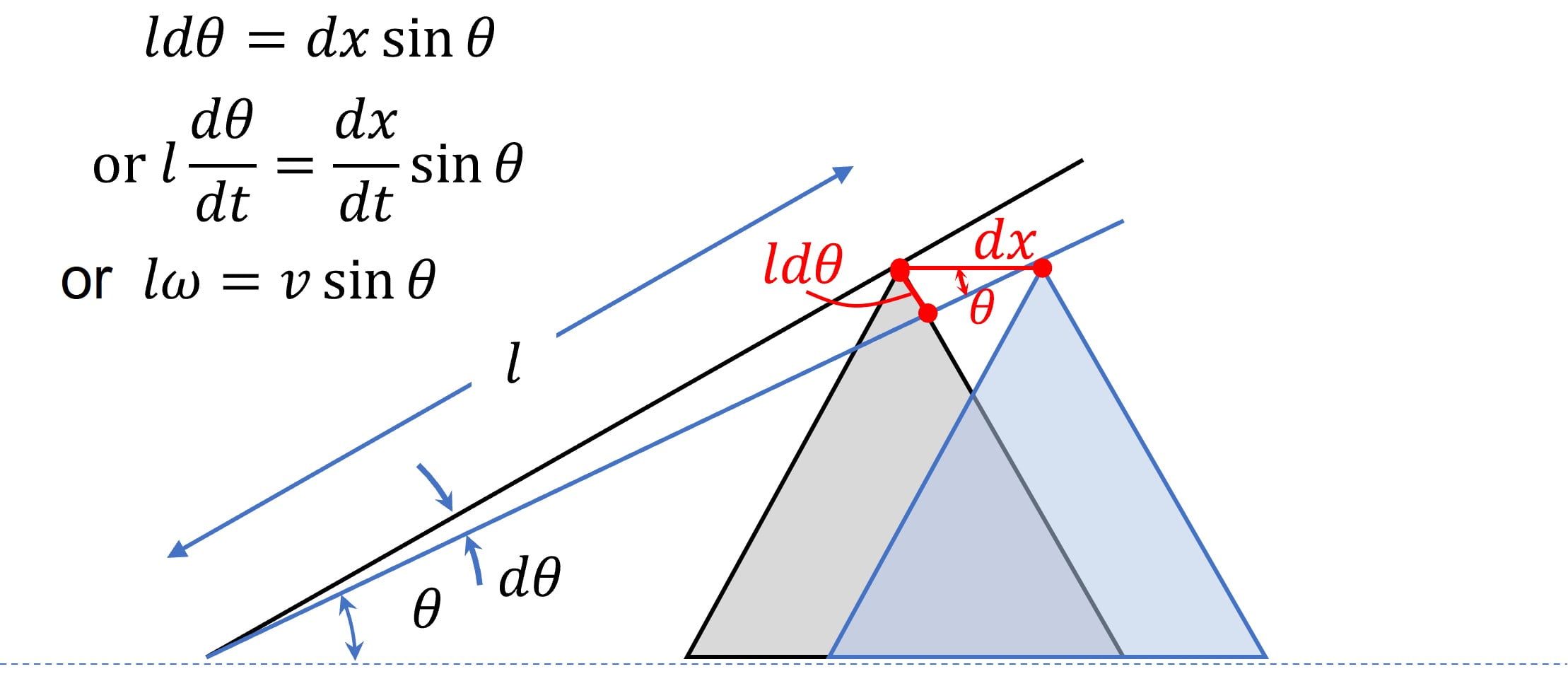
To find the angular velocity, $\omega = \cfrac{d \theta}{dt}$, let’s view the complex motion of the rod over differential time $dt$ as superposition of pure rotational motion and pure translational motion.
So, if you were to rotate the rod about end $B$ by small differential angle $d \theta$, end A is displaced by $l \ d \theta$ and this displacement makes an angle $\theta$ with the vertical
Now let’s displace the rod along x – direction by amount $dx$ such that the end $A$ lands back on the wall.
Notice the right angled triangle formed by $l \ d \theta$, $dx$, and $dy$
which then gives us the relation
$l \ d \theta \ \cos \theta = dy$
or $l \cfrac{d \theta}{dt} \cos \theta = \cfrac{dy}{dt}$
or $l \omega \cos \theta = v_A$
Correct answers are (D & C)
Question 10 (Integer Answer)
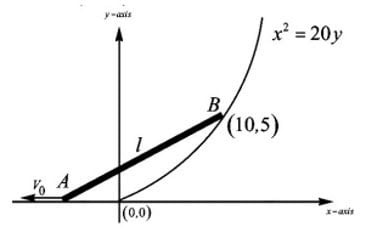
A uniform rod has mass $m=2$ kg and length $l = 13m$. One end of the rod is pulled with a constant velocity of $v_0 = 34 \ m/s$ along a frictionless horizontal floor in the negative $x$ direction. The other end is moving along a parabolic fixed curve. The equation of the parabola is $x^2 = 20y$. Find the angular velocity of the rod (in rad/s) when the end point ‘$B$’ is at ($10,5$)
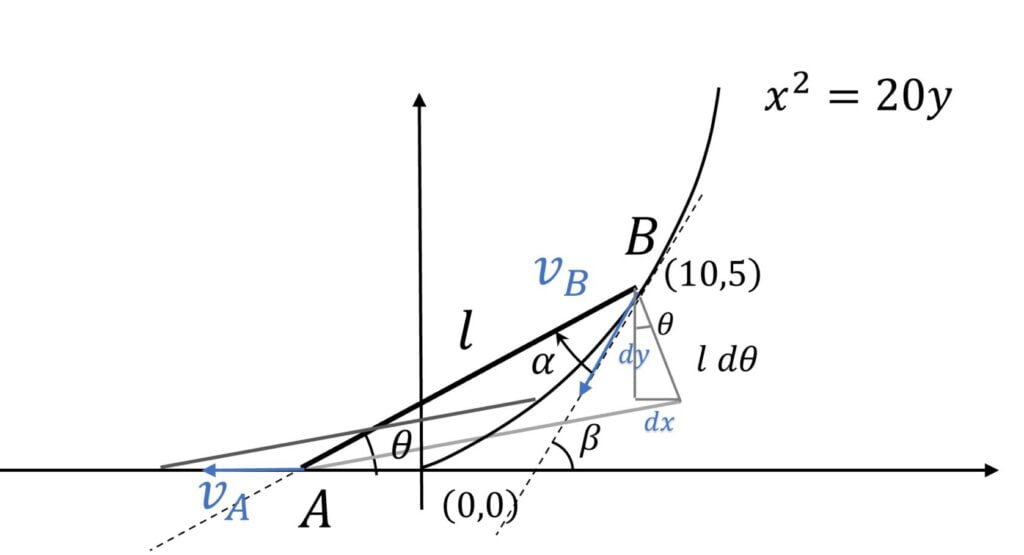
Compononent of velocity vectors of $A$ and $B$ along the rod should be the same at all times
i.e. $v_A \cos \theta = v_B \cos \alpha$
Now, to find the angular velocity $\omega = \cfrac{d \theta}{dt}$, we will need to know the angle, $\theta$ rod makes with the horiontal, when end $B$ is at $(10,5)$.
Well, $\sin \theta = \cfrac{y_B}{l}$
Now, break the complex motion of rod into superposition of pure rotational motion about end $A$ and then pure translational in the horizontal direction, which gives us the relations
$l \ d \theta \cos \theta = dy$
or $l \ \cfrac{d \theta}{dt} \cos \theta = \cfrac{dy}{dt}$
where $\cfrac{dy}{dt}$ is the vertical component of velocity of end $B$, which is simply $v_B \sin \beta$, with $\beta$ being the angle made by the tangent to the curve at $(10,5)$ with the horizontal, which can be derived using the relation, $\tan \beta = \cfrac{dy}{dx}$
Correct answer is (2)
Question 11 (Numerical Answer)
A wall is inclined to a horizontal surface at an angle of $120^{\circ}$ as shown. A rod $AB$ of length $L = 0.75$ m is sliding with its two ends $A$ and $B$ on the horizontal surface and on the wall respectively. At the moment angle $\theta = 20^{\circ}$ (see figure), the velocity of end $A$ is $V_A = 1.5 \ m/s$ towards right. Calculate the angular speed of the rod at this instant [Take $\cos 40^{\circ} = 0.766$]
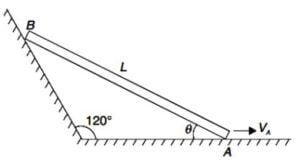
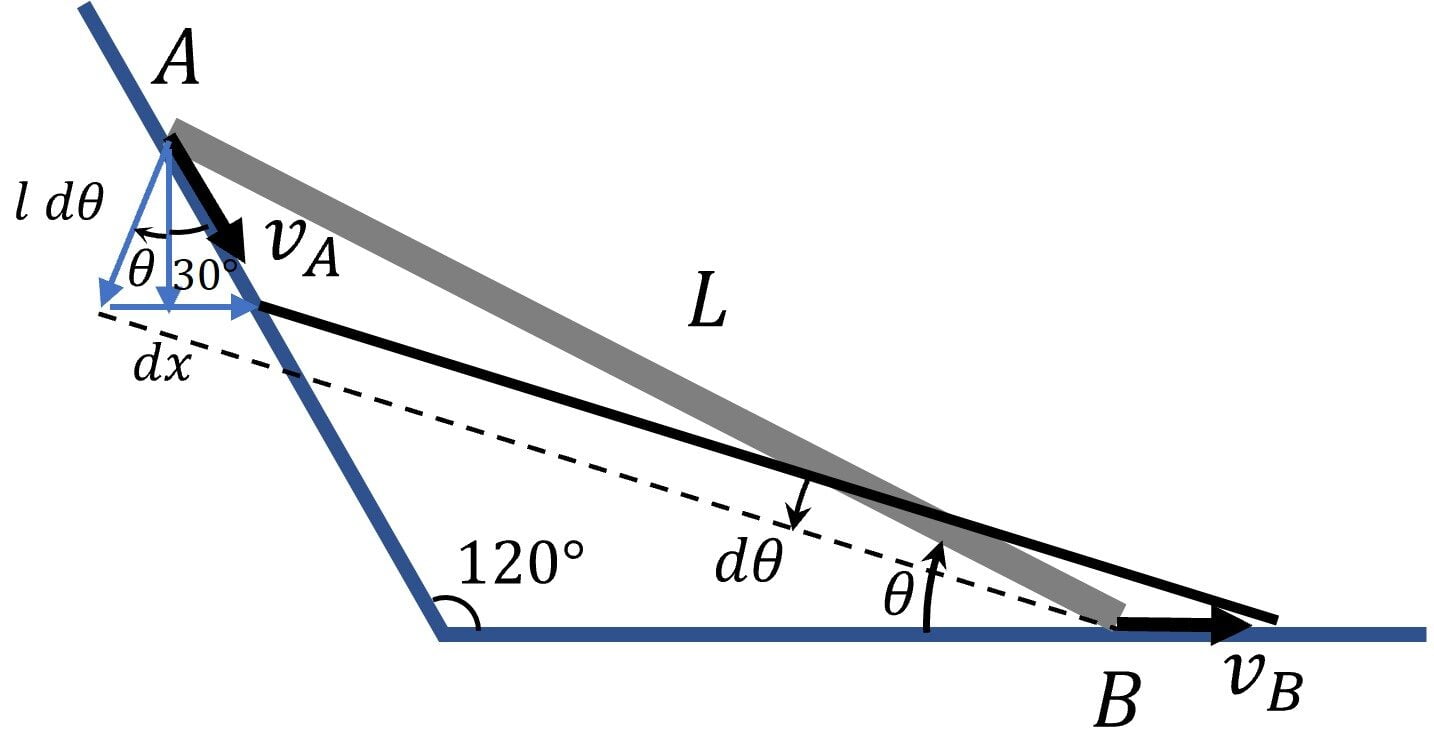
To begin with, let’s establish the velocity of end $B$, for which we will use the fact that the component of their velocities along the rod should be the same
i.e. $v_A \cos (60 – \theta) = v_B \cos \theta$
Now, to determine the angular velocity, let’s view this complex motion as superposition of pure differential rotational motion about $B$ followed by pure differential translational motion, which gives the relation
$v_A \cos 30 = l \cfrac{d \theta}{dt} \cos \theta$
Correct answer is (2.26)
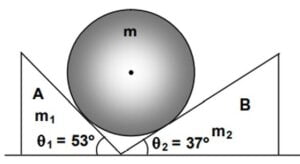
Question 12 (More than one correct answers)
Two smooth triangular wedges $A$ and $B$ of masses $m_1 = 9$ kg and $m_2 = 16$ kg and inclination $\theta_1 = 53^{\circ}$ and $\theta_2 = 37^{\circ}$ respectively are placed on a smooth horizontal surface touching each other at their bottom edges. A horizontal cylinder of mass $m = 25$ kg is placed on the triangular wedges and then released from rest. When the centre of mass of the cylinder fallls through height $h = 0.4$ m, then at this instant which of the following statements is/are correct.
(A) The velocity of the wedge ‘$A$’ is $2$ m/s
(B) The velocity of the wedge ‘$B$’ is $1$ m/s
(C) The velocity of the cylinder is $1$ m/s
(D) The velocity of the cylinder is $2$ m/s
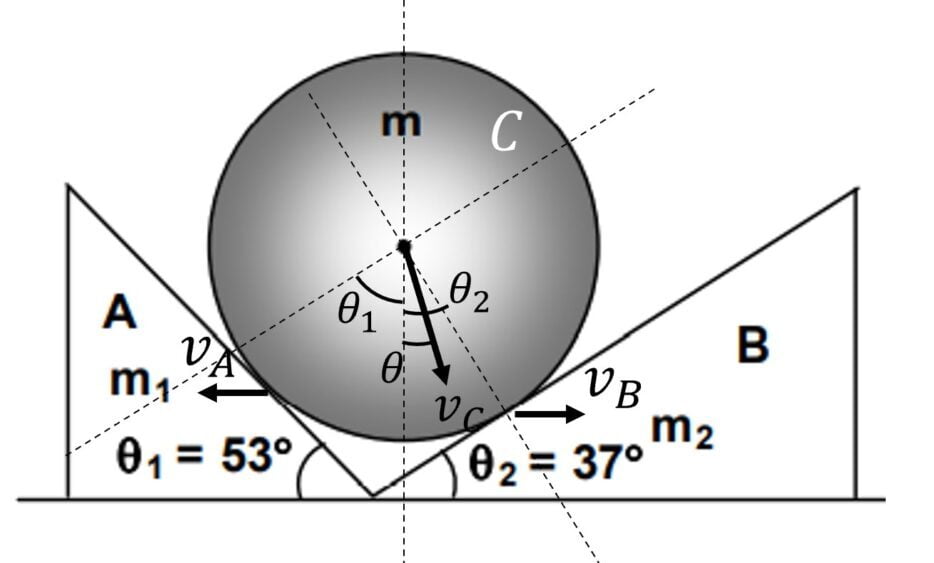
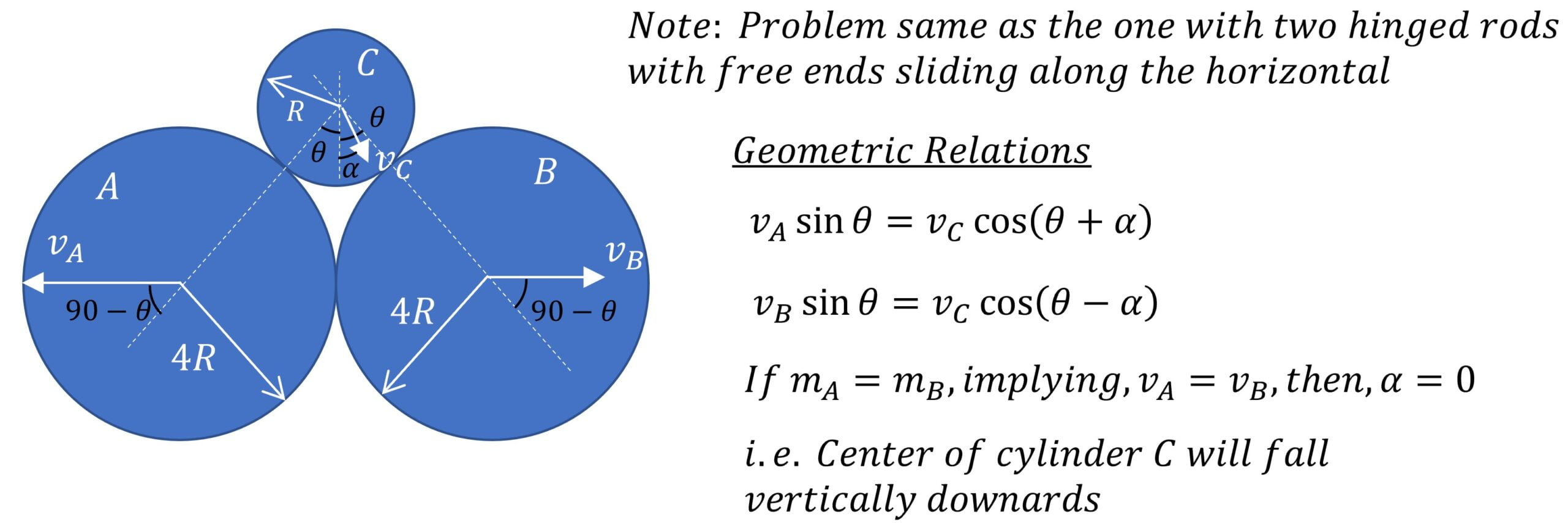
Using the fact that the component of velocity of cylinder and any of the wedge in teh direction perpendicular to the inclined surface of that wedge, give us two key relations
$v_A \sin \theta_1 = v_C \cos (\theta_1 + \theta)$
$v_B \sin \theta_2 = v_C \cos (\theta_2 – \theta)$
Additionally, since there is no force on the wedges, cylinder system in the horizontal direction, the momentum of the system in the horizontal direction would remain conserved i.e.
$m_1 v_A = m_2 v_B + m v_C \sin \theta$
Now since there are no dissipative forces acting on the system, mechanical energy of the system should remain conserved
i.e. $mgh = \cfrac{1}{2} m_1 v_A^2 + \cfrac{1}{2} m_2 v_B^2 + \cfrac{1}{2} m v_C^2$
Correct answer are (A,D)
Question 13 (Integer Answer)
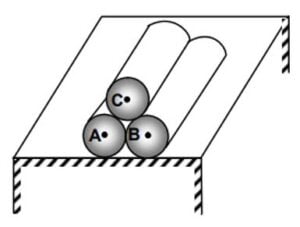
Radius of cylinder $A$ and $B$ are same and equal to $4R$ while the radius of cylinder $C$ is $R$. All three cylinders are released from rest. Magnitude of acceleration of cylinder $A$ is $a_1$ and that of cylinder $C$ is $a_2$. If the ratio of $\cfrac{a_1}{a_2}$ is $\cfrac{k}{4}$, then find the value of $k$. (all the surfaces are frictionless)
Question 14 (Numerical Answer)
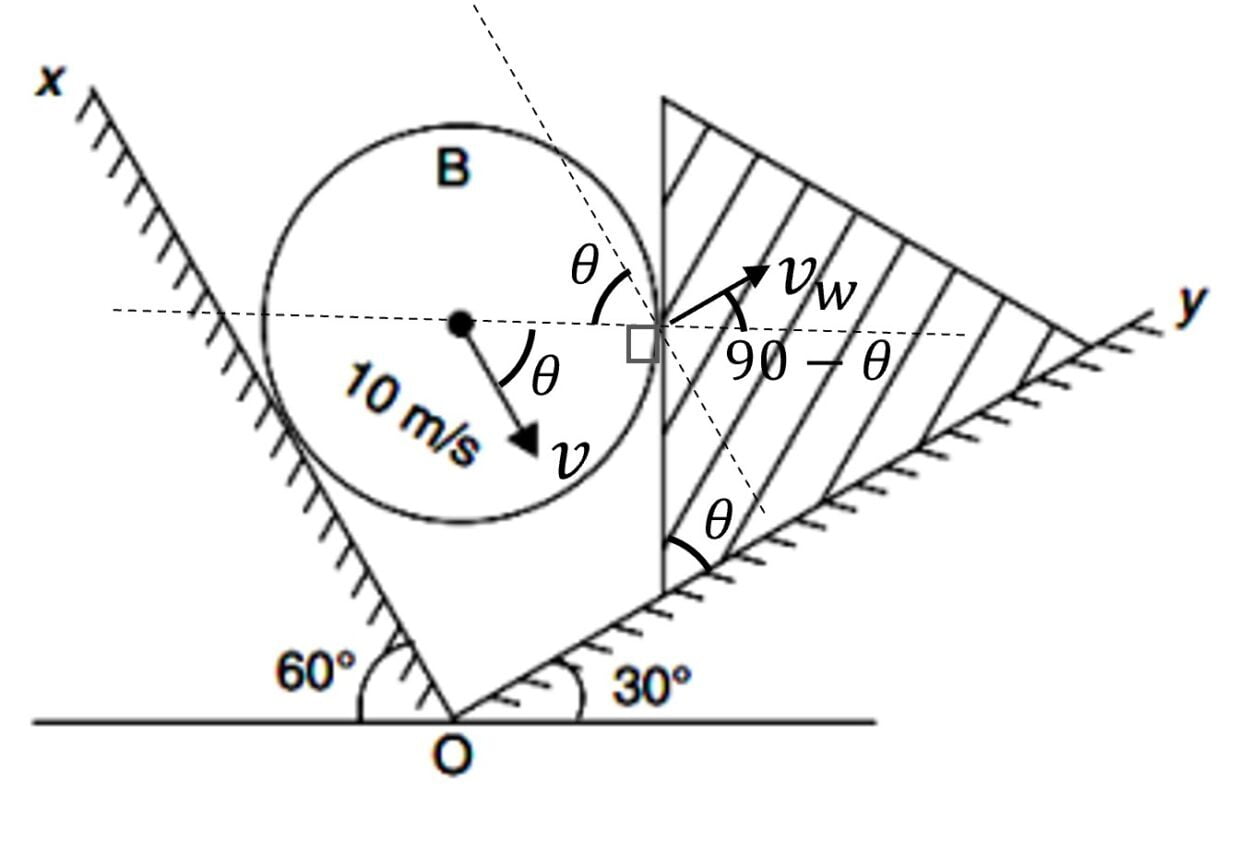
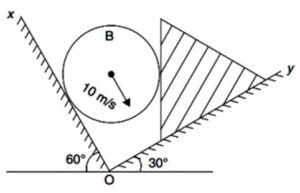
In the arrangement shown in the figure $A$ is an equilateral wedge and the ball $B$ is rolling down the incline $XO$. Find the velocity of the wedge (of course along $OY$) at the moment velocity of the ball is $10$ m/s parallel to the incline $XO$.
Question 15
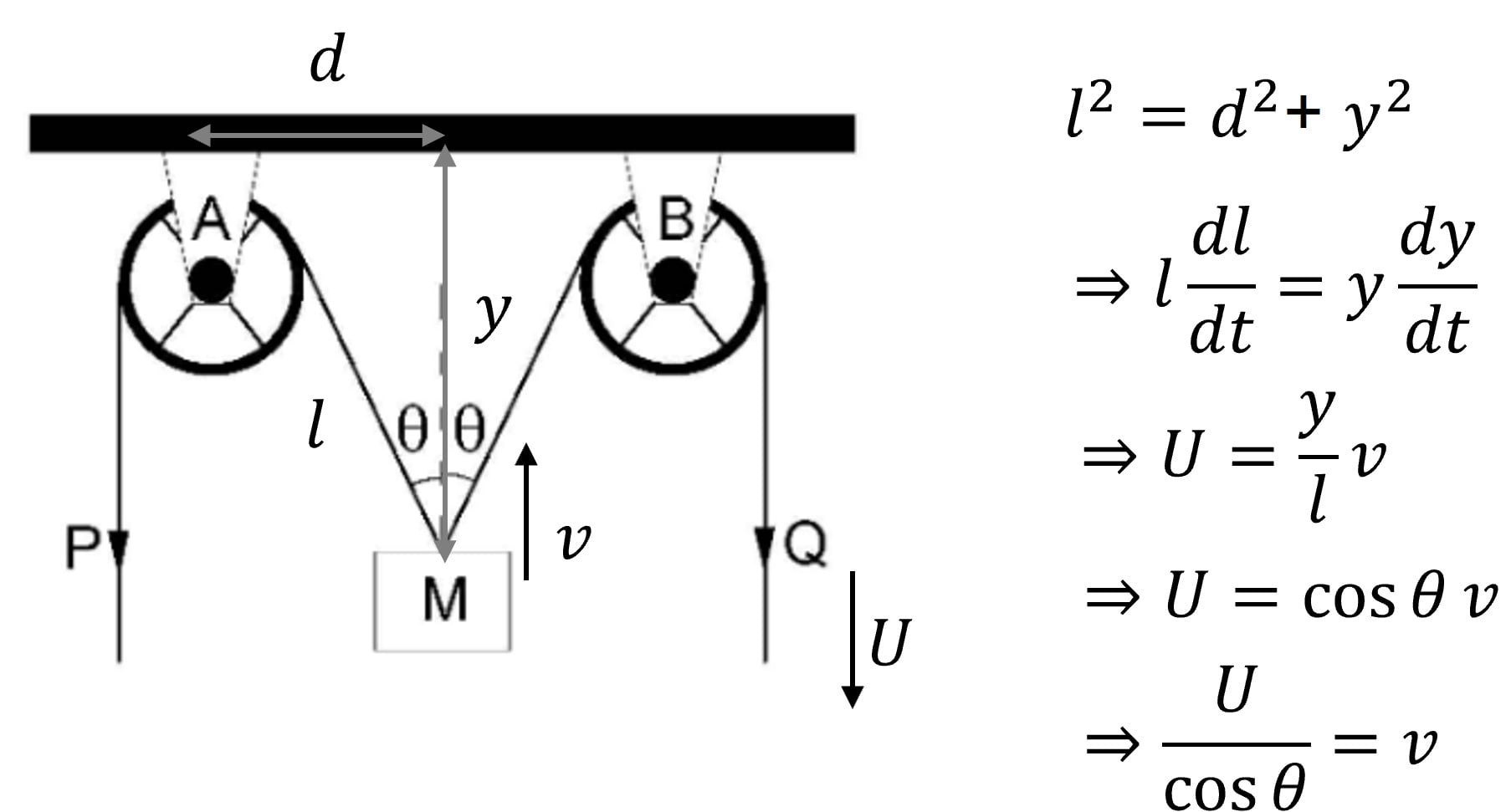
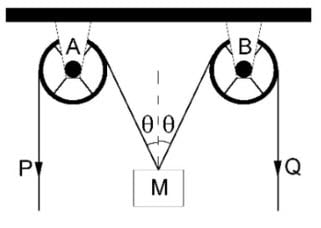
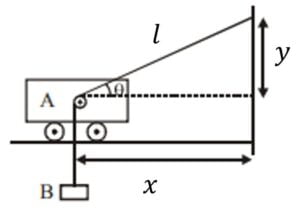
In the arrangement shown in the figure, the ends $P$ and $Q$ of an unstretchable string, move downwards with uniform speed $U$. Pulleys $A$ and $B$ are fixed. Mass $M$ move upwards with a speed:
Question 16 (Only one correct answer)
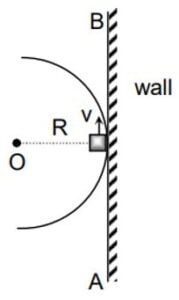
As shown in the figure, $AB$ represents an infinite wall tangential to horizontal semi-circular track. $O$ is a point source of light on the ground at the centre of the circle. A block moves along the circular track with a constant speed $v$ starting from the point where the wall touches the circular track. Then the acceleration of the shadow of the block along the length of wall is
(A) zero
(B) $\left( \cfrac{v^2}{R} \right) \ \sec^2 \left( \cfrac{vt}{R} \right) \ \tan \left( \cfrac{vt}{R} \right) $
(C) $\left( \cfrac{v^2}{2R} \right) \ \sec^2 \left( \cfrac{vt}{R} \right) \ \tan \left( \cfrac{vt}{R} \right) $
(D) $\left( \cfrac{2v^2}{R} \right) \ \sec^2 \left( \cfrac{vt}{R} \right) \ \tan \left( \cfrac{vt}{R} \right) $
Question 17 (More than one correct answers)
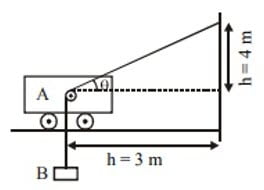
The string shown in the figure is passing over small smooth pulley rigidly attached to trolley $A$. If speed of trolley is constant and equal to $V_A$. Speed and magnitude of acceleration of block $B$ at the instant shown in figure is
(A) $v_B = v_A$, $a_B = 0$
(B) $a_B = 0$
(C) $v_B = \cfrac{3}{5} v_A$
(D) $a_B = \cfrac{16 v_A^2}{125}$
For any position of the trolley $A$, $x^2 + y^2 = l^2$
Differentiating it with respect to time $t$, we get
$l \cfrac{dl}{dt} = x \cfrac{dx}{dt}$
(Note: $y$ is constant)
i.e. $l v_B = x v_A$
Differentiating it with respect to time $t$ one more time, we get
$\cfrac{dv_B}{dt} = \cfrac{1}{l} (v_A^2 – v_B^2)$ $= \cfrac{v_A^2}{l} (1 – \cfrac{x^2}{l^2})$
Correct answer are (C, D)
Question 18 (More than one correct answers)
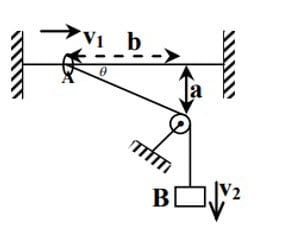
Ring $A$ can slide on a smooth horizontal rod and block $B$ can move vertically. Both are attached by an inextensible string. At a certain instant velocity of ring is $v_1$ and of block is $v_2$. At that instant ring is at a horizontal distance $b$ from pulley as shown. Then
(A) $v_2 = v_1 \cos \theta$
(B) $a_2 = a_1 \cos \theta$, where $a_2$ and $a_1$ represent the accelerations of block and ring respectively at that instant
(C) $v_1 = v_2 \cos \theta$
(D) Angular velocity of the ring with respect to an observer on the pulley is $\cfrac{v_1 \sin \theta}{\sqrt{a^2 + b^2}}$
Correct answers are (A,D)
Question 19 (Integer Answer)
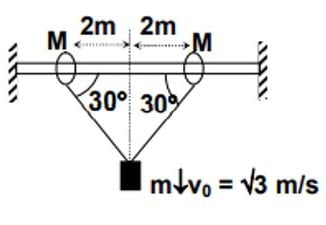
Two rings, each of mass $M = 100$ gm are constrained to move along a fixed horizontal rod. An ideal string is connected with rings and a small $m = 200$ gm is connected to the mid-point of string. At any moment $m$ is moving downward with velocity $\sqrt{3}$ m/s. The speed of ring of $M$ at the same moment is
Correct answer is (1)
Question 20 (Numerical Answer))
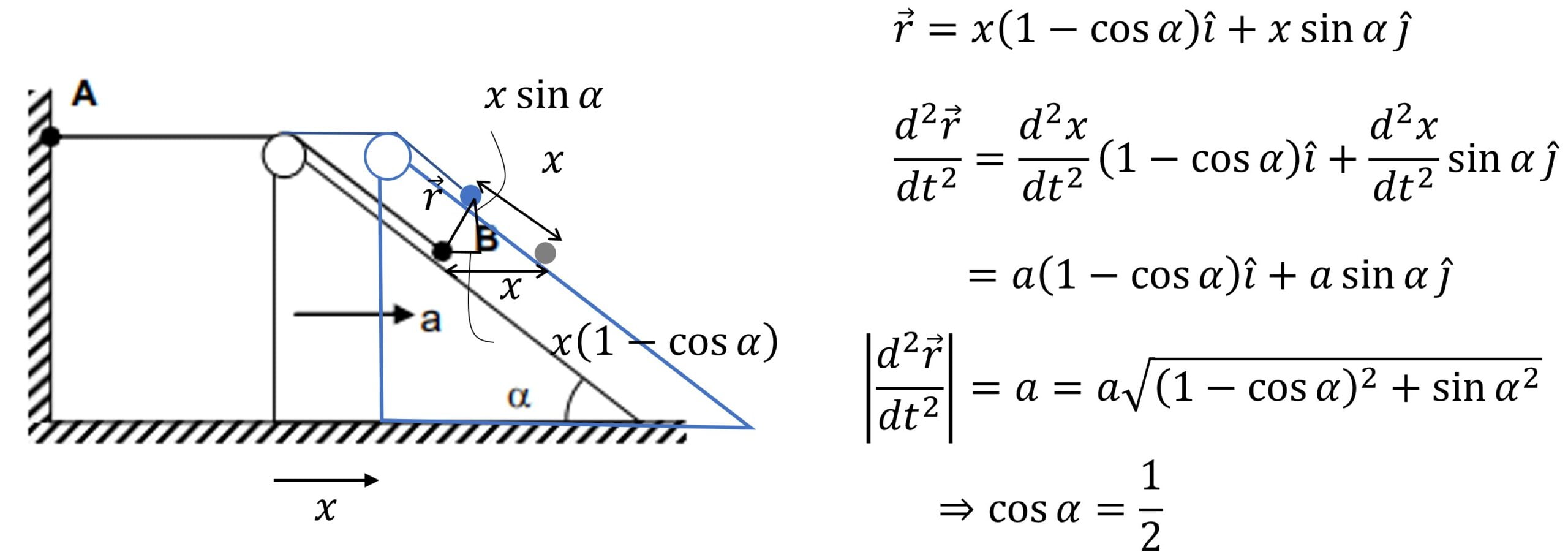
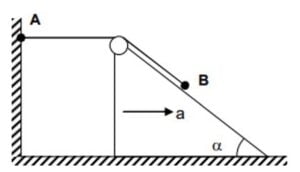
A weightless inextensible rope rests on a stationary wedge forming an angle $\alpha$ with the horizontal. One end of the rope is fixed to the wall at point $A$. A small load is attached to the rope at point $B$. Wedge starts moving to the right with a constant acceleration $a$ and same is the magnitude of acceleration of load. $\alpha$ (in degree) is
Question 21 (More than one correct answer)
A string of length ‘$2a$’ has been tied at $A$ and $B$ such that $AB$ $=$ ‘$a$’. The string is passing through a bead $C$ and initially the bead is very close to $A$. Now the bead is allowed to fall. Let $h$ be the height by which bead falls when the string becomes taut and $v$ be the speed of the bead just after the string becomes taut. Pick correct option(s):
(A) $v = \sqrt{3ag} \sin (26.5^{\circ})$
(B) $v = \sqrt{ag} \sin 26.5^{\circ})$
(C) $h = \cfrac{3a}{5}$
(D) $h = \cfrac{3a}{4}$
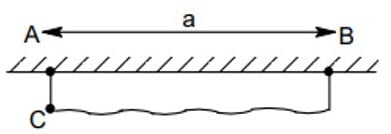
Correct answer are (B,D)