Physics NLM problems, i.e., practice problems on newton’s laws of motion. Note that you can expect up to one question from this topic in JEE Main and JEE Advanced. But more importantly, this topic is foundational for other physics topics, so it is important that you develop a good comfort with this topic
Q1 Two blocks of mass $m = 5 \ kg$ and $M = 10 \ kg$ are connected by a string passing over a pulley $B$ as shown. Another string connects the center of pulley $B$ to the floor and passes over another pulley $A$ as shown. An upward force $F$ is applied at the center of pulley $A$. Both the pulleys are massless.
Find the acceleration of blocks $m$ and $M$ if $F$ is :
(a) $100 \ N$
(b) $300 \ N$
(c) $500 \ N$ (take $g = 10 \ m/s^2$)

Correct answers are
(a) $0, \ 0$
(b) $5 \ m/s^2, \ 0$
(c) $15 \ m/s^2, \ 2.5 \ m/s^2$
Q2 Three blocks of mass $m_1, \ m_2$ and $m_3$ are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of $m_1$.
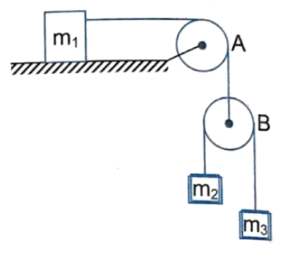
Correct answer is $\cfrac{g}{1 + \cfrac{m_1}{4}\left(\cfrac{1}{m_2} + \cfrac{1}{m_3}\right)}$
Q3 Consider the situation shown in the figure. The horizontal surface below the bigger block is smooth. The coefficient of friction between the blocks is $\mu$. Find the minimum and the maximum force $F$ that can be applied in order to keep the smaller blocks at rest with respect to the bigger block.
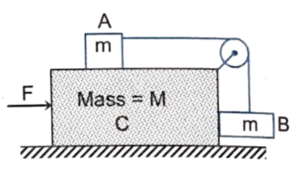
Correct answers are
$F_{\text{min}} = \cfrac{1 – \mu}{1 + \mu}(M + 2m)g$
$F_{\text{max}} = \cfrac{1 + \mu}{1 – \mu}(M + 2m)g$
Q4 A block of mass $1 \ kg$ is pushed against a rough vertical wall with a force of $20 \ N$. Coefficient of static friction being $\cfrac{1}{4}$. Another horizontal force of $10 \ N$ is applied on the block in a direction parallel to the wall. Will the block move ? If yes, with what acceleration ? If no, find the frictional force exerted by the wall on the block. ($g = 10 \ m/s^2$).
Correct answer is
Yes, $a = 9.14 \ m/s^2$
Q5 Figure shows two blocks connected by a light string placed on the two inclined parts of a triangular wedge. The coefficients of static and kinetic friction are $0.28$ and $0.25$ respectively at each of the surfaces.
(a) Find the minimum and maximum values of $m$ for which the system remains at rest.
(b) Find the acceleration of either block if $m$ is given the minimum value calculated in the first part and is gently pushed up the inclined for a short while $g = 10 \ m/s^2$
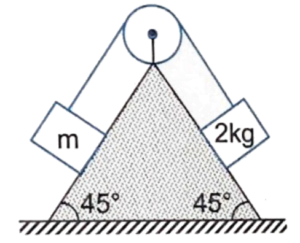
Correct answers are
(a) $9/8 \ kg, \ 32/9 \ kg$
(b) $0.21 \ m/s^2$
Q6 A block of mass $3 \ kg$ is in equilibrium with the help of three identical strings with one end of each string connected with the ceiling and other with the block and the angle between any two string is $120^{\circ}$ and all the string makes an angle of $60^{\circ}$ with the vertical. Find the tension in the string.
Correct answer is $20$ Newton
Q7 Figure shows overhead views of four situations in which forces act on a block that lies on a frictionless floor. If the force magnitudes are chosen properly, in which situation is it possible that the block is (i) stationary and (ii) moving with a constant velocity ?

Correct answers are
(i) b and d, (ii) b and d
Q8 Give the magnitude and direction of the net forces acting on:
(a) A stone of mass $0.1 \ kg$ just after it is dropped from the window of a stationary train.
(b) The same stone as above just after it is dropped from the window of train running at a constant velocity of $36 \ km/hr$
(c) The same stone as above just after it is dropped from the window of a train accelerating with $1 \ m/s^2$
(d) The same stone as above lying on the floor of a train which is accelerating with $1 \ m/s^2$, the stone being at rest relative to the train. Neglect air resistance throughout, and take $g = 9.8 \ m/s^2$
Correct answers are
(a) $m = 0.1 \ kg; \ a = g = 9.8 \ m/s^2$
Net force, $F = mg = 0.1 \times 9.8 = 0.98 \ N$ vertically downward on the stone.
(b) Net force $ = 0.1 \ kg \times 9.8 \ m/s^2 = 0.98 \ N$ on the stone vertically downwards.
(c) Net force $ = 0.1 \ kg \times 9.8 \ m/s^2 = 0.98 \ N$ vertically downwards.
(d) Net force $ = m \times a = 0.1 \ kg \times 1 \ m/s^2 = 0.1 \ N$ along the direction of the motion of the train.
Q9 A block is resting on a horizontal plate in the $xy$ plane and the coefficient of friction between block and plate is $\mu$. The plate begins to move with velocity $u = bt^2$ in $x$ direction. At what time will the block start sliding on the plate.
Correct answer is $\cfrac{\mu g}{2b}$
Q10 A block of mass $6 \ kg$ is kept on rough surface as shown in figure. Find acceleration and friction force acting on the block. (Take $g = 10 \ m/s^2$)
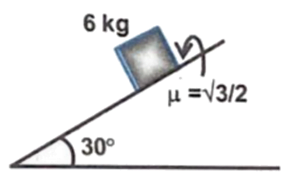
Correct answers are $a = 0, \ f = 30 \ N$
Q11 The two blocks $m = 5 \ kg$ and $M = 25 \ kg$ as shown in the figure are free to move. The co-efficient of friction between the blocks is $\mu_s = 0.4$, but the co-efficient of friction between ground and $M$ is frictionless. What is the minimum horizontal force $F$ required to hold $m$ against $M$ ?
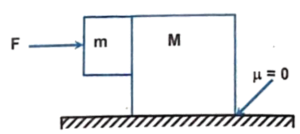
Correct answer is $150 \ N$
Q12 The frictional co-efficient between the board and the floor shown in figure is $\mu$. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor. The mass of man is $M$ and the mass of block is $m$
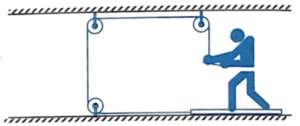
Correct answer is $\cfrac{\mu(M + m)g}{1 + \mu}$
Q13 A truck shown in the figure is driven with an acceleration $a = 3 \ m/s^2$. Find the acceleration of the bodies $A$ and $B$ of masses $10 \ kg$ and $5 \ kg$ respectively, assuming pulleys are massless and friction is absent everywhere.
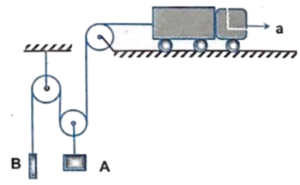
Correct answer is $a_A = a_B = 1 \ m/s^2 $ upwards
Q14 A car moves with constant tangential acceleration $a_T = 0.80 \ m/s^2$ along a horizontal surface circumscribing a circle of radius $R = 40 \ m$. The co-efficient of sliding friction between the wheels of the car and the surface is $\mu = 0.20$. What distance will the car move without sliding if its initial velocity is zero ?
Correct answer is $45.82 \ m$
Q15 In the arrangement shown in figure $m_A = m$ and $m_B = 2m$, while all the pulleys and string are massless & frictionless. At $t = 0$, a force $F = 10 \ t$ starts acting over central pulley in vertically upward direction. Find
(a) Time at which both the masses lose contact with floor.
(b) Velocity of $A$ when $B$ loses contact with floor.
[Take all the units into S.I. system, take $m = 1 \ kg$ and $g = 10 \ m/s^2$ for part (b)]
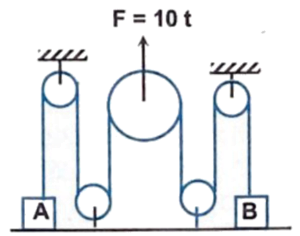
Correct answers are
(a) $\cfrac{2mg}{5} \ s$
(b) $10 \ m/s$
Q16 Three blocks $m_1 = 3 \ kg, \ m_2 = 2 \ kg, \ m_3 = 5 \ kg$, lie on an inclined frictionless surface as shown in the figure. (Take $g = 10 \ m/s^2$)
(a) What force $(F)$ parallel to the incline is needed to push the blocks up the plane with an acceleration $a = 2 \ m/s^2$ ?
(b) Find the contact force between $m_1$ & $m_2$ and $m_2$ & $m_3$. When the blocks are moving up with an acceleration of $2 \ m/s^2$ up the inclined.
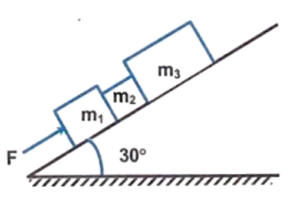
Correct answers are
(a) $70 \ N$
(b) $49 \ N, \ 35 \ N$
Q17 A balloon is descending with a constant acceleration $’a’$ less than the acceleration due to gravity. The mass of the balloon, with its basket and contents is $M$. What mass $m$, of ballast (sand bags) should be released so that the balloon will begin to accelerate upward with constant acceleration $’a’$ ? (Neglect air resistance)
Correct answer is $m = \cfrac{2Ma}{g + a}$
Q18 A ball is held at rest in position $A$ as shown in the figure by two light cords. The horizontal cord is cut and the ball swings as a pendulum. What is the ratio of the tensions in the supporting cord, in position $A$, to that in position $B$ ?
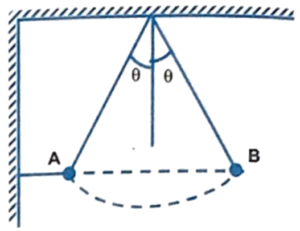
Correct answer is $\cfrac{T_A}{T_B} = \sec^2 \theta$
Q19 If the coefficient of friction between an insect and bowl is $\mu$ and the radius of the bowl is $r$, find the maximum height to which the insect can crawl in the bowl.
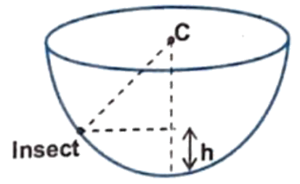
Correct answer is $r\left[1 – \cfrac{1}{\sqrt{1 + \mu^2}}\right]$
Q20 A block of mass $m = 1 \ kg$ rests on a wedge of mass $M = 9 \ kg$, which in turn is placed on a table as shown in the figure. All the surfaces are smooth.
(a) What horizontal acceleration $’a’$ must $M$ have relative to the stationary table so that $m$ remains stationary relative to the wedge ?
(b) Find the horizontal force required to maintain this acceleration.
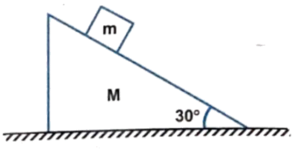
Correct answers are
(a) $5.658 \ m/s^2$ rightward,
(b) $56.58 \ N$