Given a two-dimensional variable force $\overrightarrow{F}(x,y)$ acting on a particle moving along a given curved path or moving along an unknown path, how would you determine the work done by this variable force as the particle moves from point $A$ to point $B$
$\color{blue}{\text{Solution Steps}}$
$W = \int \overrightarrow{F}.\overrightarrow{ds}$ $=\int (f_x(x,y) \hat{i} +$ $f_y(x,y) \hat{j}).$$(dx \hat{i} +$ $dy \hat{j})$ $=\int f_x(x,y) dx +$ $f_y(x,y) dy$
Now depending on the given expressions for $f_x(x,y)$ and $f_y(x,y)$, there are 3 ways we can approach the problem to find the work done
a) If $f_x(x,y) = f(x)$ and $f_y(x,y) = g(y)$, then $W=\int (f_x(x,y) dx +$ $f_y(x,y) dy)$ $=\int_{x_i}^{x_f} f(x) dx +$ $\int_{y_i}^{y_f} g(y) dy$
For example, let’s say that $\overrightarrow{F} = $ $x \hat{i} +$ $y \hat{j}$, then $W=$ $=\int_{x_i}^{x_f} x dx +$ $\int_{y_i}^{y_f} y dy$, which you can easily solve.
Note that if you were given $\overrightarrow{F} = $ $K(\cfrac{x}{(x^2+y^2)^{1/2}} \hat{i} +$ $\cfrac{y}{(x^2+y^2)^{1/2}} \hat{j})$ and it was also given that particle is moving along a circular path of radius ‘$a$’, centered at origin, then recall that $(x^2+y^2)^{1/2} = a$ and so, we can write $\overrightarrow{F} = $ $\cfrac{K}{a}(x \hat{i} +$ $y \hat{j})$ and the rest of the steps for finding $W$ will be same as mentioned above.
b) If $f_x(x,y)$ and $f_y(x,y)$ are such that $f_x(x,y) dx + f_y(x,y)dy$ can be expressed as exact differential, i.e. $f_x(x,y) dx + f_y(x,y)dy$ $=d(g(x,y))$ then $W=\int f_x(x,y) dx +$ $f_y(x,y) dy$ $=\int_{x_i, \ y_i}^{x_f, \ y_f} d(g(x,y))$ $=g(x_f,y_f) – g(x_i,y_i)$
Recall that $\cfrac{d(AB)}{dt} =A \cfrac{d(B)}{dt} + B\cfrac{d(A)}{dt}$
Or, $d(AB) = Ad(B) + Bd(A)$
For example, let’s say that $\overrightarrow{F} = $ $xy^2 \hat{i} +$ $x^2y \hat{j}$, then $W=\int (xy^2 dx +$ $x^2y dy)$ $=\int_{x_i, \ y_i}^{x_f, \ y_f} d(\cfrac{1}{2}x^2y^2)$ $=\cfrac{1}{2}(x_f^2y_f^2 – x_i^2y_i^2)$
c) If $f_x(x,y)$ and $f_y(x,y)$ are such that we CANNOT express $f_x(x,y) dx + f_y(x,y)dy$ as exact differential and if the trajectory of the path is specified, say for example $(x-a)^2+(y-b)^2 = c^2$
Then, to solve $W=\int f_x(x,y) dx +$ $f_y(x,y) dy$, we will write $y$ in terms of $x$ using the equation of trajectory for $f_x$ and write $x$ in terms of $y$ for $f_y$, then we should be able to integrate the two terms. Here you will need to be careful when writing $x$ in terms of $y$ or vice versa for the given trajectory as the expression might be different for different parts of the trajectory, so break the integral limits as appropriate and then integrate.
Work done by a variable force | Sample Problems
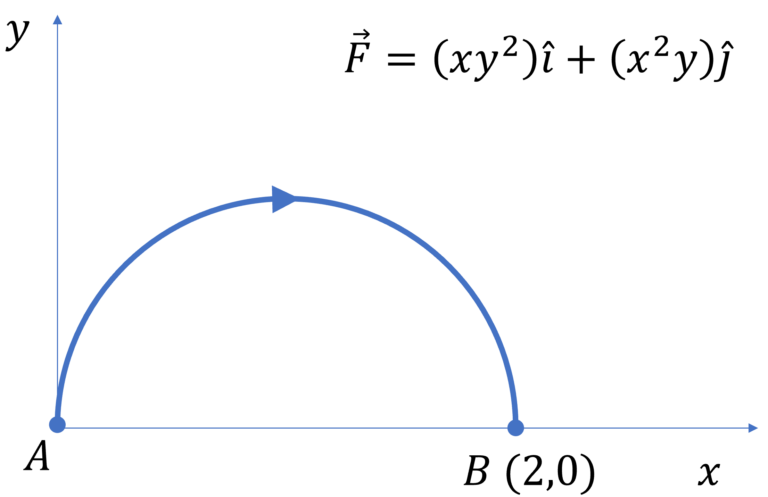
Q1 Given $\overrightarrow{F}=$ $xy^2 \hat {i} + x^2y \hat{j}$ newtons, find the work done by $\overrightarrow{F}$ when a particle is taken along the semicircular path $AB$ where the coordinates of $B$ are ($2,0$)

Zero.
$W = \int F_x dx + F_y dy$ $=\int (xy^2 dx +$ $x^2y dy)$ $=\int_{x_i, \ y_i}^{x_f, \ y_f} d(\cfrac{1}{2}x^2y^2)$ $=\cfrac{1}{2}(x_f^2y_f^2 – x_i^2y_i^2) = \cfrac{1}{2}(4.0-0.0) = 0$
Q2. Particle moves from point A to point B along the line shown in figure under the action of force $\overrightarrow{F}$ $=−x \hat{i} + y \hat{j}$. Determine the work done on the particle by $\overrightarrow{F}$ in moving the particle from point $A$ to point $B$ (all quantities are in SI units).
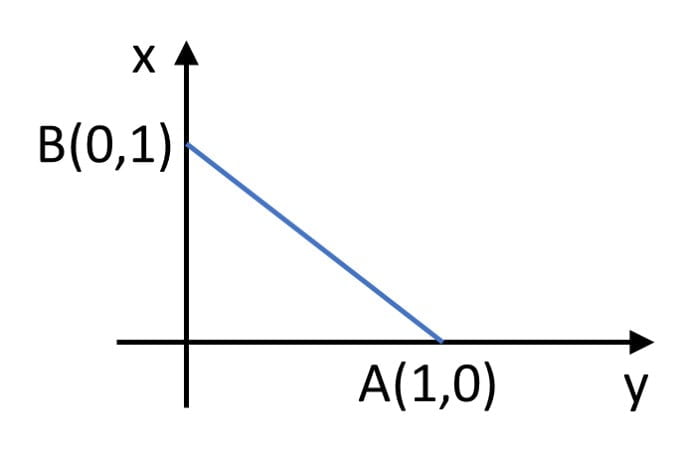
1J
$W = \int F_x dx + F_y dy$ $=\int (-x dx +$ $y dy)$ $=-\int_{1}^{0} xdx$ $+\int_{0}^{1} ydy$