Here we will review the steps involved in establishing capacitance of a parallel plate capacitor with dielectric slab for the following 5 scenarios
1) Parallel plate capacitor with two dielectric slabs in series
2) Parallel plate capacitor with two dielectric slabs in parallel
3) Parallel plate capacitor with multiple dielectric slabs in series and parallel
4) Parallel plate capacitor with triangular dielectric slab
5) Parallel plate capacitor with dielectric slab of varying dielectric strength (along the gap between capacitor plates)
Parallel plate capacitor with two dielectric slabs in series
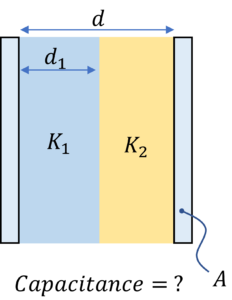
Approach 1: Imagine a metallic plate of very small thickness between the two dielectrics, then we can think of this setup as two capacitors ($C_1$ and $C_2$) in series where
$C_1 = \cfrac{K_1 \epsilon_0 A}{d_1}$, and
$C_2 = \cfrac{K_2 \epsilon_0 A}{d – d_1}$
Now for two capacitors $C_1$ and $C_2$ in series, equivalent capacitance, $C_{eq}$ is given by $\cfrac{1}{C_{eq}} = \cfrac{1}{C_1} + \cfrac{1}{C_2}$
Or, $C_{eq} = \epsilon_0 A \cfrac{K_1 K_2}{K_2 d_1 + K_1 (d – d_1)}$
Approach 2: Let’s work out the effective capacitance from the basics
$C_{eq} = \cfrac{Q}{V}$, where $Q$ is the magnitude of charge on capacitor plates and $V$ is the potential difference between two plates
Now, $|V| = \int \overrightarrow{E}.\overrightarrow{dl}$ $= \int_0^{d_1} E dx + \int_{d_1}^d E dx$
In the region $0 \leq x \leq d_1$, $E = \cfrac{\sigma}{K_1 \epsilon_0}$ $= \cfrac{Q}{K_1 \epsilon_0 A}$
In the region $d_1 \leq x \leq d$, $E = \cfrac{\sigma}{K_2 \epsilon_0}$ $= \cfrac{Q}{K_2 \epsilon_0 A}$
So, $V = \cfrac{Q d_1}{K_1 \epsilon_0 A} + \cfrac{Q (d – d_1)}{K_1 \epsilon_0 A}$
Thus, $C_{eq} = \cfrac{Q}{V}$ $= \epsilon_0 A \cfrac{K_1 K_2}{K_2 d_1 + K_1 (d – d_1)}$
Parallel plate capacitor with two dielectric slabs in parallel
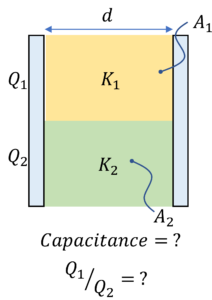
Approach 1: We can think of this setup as two capacitors ($C_1$ and $C_2$) in parallel where
$C_1 = \cfrac{K_1 \epsilon_0 A_1}{d}$, and
$C_2 = \cfrac{K_2 \epsilon_0 A_2}{d}$
Now for two capacitors $C_1$ and $C_2$ in parallel, equivalent capacitance, $C_{eq}$ is given by $C_{eq} = C_1 + C_2$
Or, $C_{eq} = \cfrac{\epsilon_0}{d} (K_1 A_1 + K_2 A_2)$
Approach 2: Now let’s work out the effective capacitance from the basics
$C_{eq} = \cfrac{Q}{V}$ $=\cfrac{Q_1 + Q_2}{V}$, where $Q_1$ is the magnitude of charge on part of the capacitor plates with dielectric of dielectric strength $K_1$ sandwiched between them, $Q_2$ is the magnitude of charge on part of the capacitor plates with dielectric of dielectric strength $K_2$ sandwiched between them, and $V$ is the potential difference between two plates
Now, $|V| = \int \overrightarrow{E}.\overrightarrow{dl}$ $= E_1 d$ $= E_2 d$
where $E_1$ is the electric field in the region with dielectric $K_1$ and $E_2$ is the electric field in the region with dielectric $K_2$
Now, $E_1 = \cfrac{\sigma_1}{K_1 \epsilon_0}$ $=\cfrac{Q_1}{K_1 A_1 \epsilon_0}$, and
$E_2 = \cfrac{\sigma_2}{K_2 \epsilon_0}$ $=\cfrac{Q_2}{K_2 A_2 \epsilon_0}$
So, $V = \cfrac{Q_1 d}{K_1 A_1 \epsilon_0}$ $= \cfrac{Q_2 d}{K_2 A_2 \epsilon_0}$
Or $Q_1 + Q_2 = V \cfrac{\epsilon_0 (A_1 K_1 + A_2 K_2)}{d}$
Or $C_{eq} =$ $\cfrac{Q_1+Q_2}{V}$ $= \cfrac{\epsilon_0 (A_1 K_1 + A_2 K_2)}{d}$
Parallel plate capacitor with multiple dielectric slabs in series and parallel
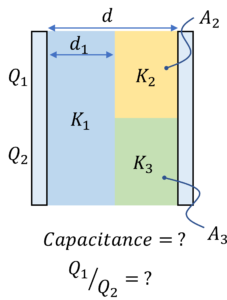
Approach 1: We can think of this setup as two capacitors ($C_1$ and $C_2$) in parallel where
$\cfrac{1}{C_1} = \cfrac{d_1}{K_1 \epsilon_0 A_1} + \cfrac{d_2}{K_2 \epsilon_0 A_1}$, and
$\cfrac{1}{C_2} = \cfrac{d_1}{K_2 \epsilon_0 A_2} + \cfrac{d_2}{K_3 \epsilon_0 A_2}$
Now for two capacitors $C_1$ and $C_2$ in parallel, equivalent capacitance, $C_{eq}$ is given by $C_{eq} = C_1 + C_2$
Or, $C_{eq} = \epsilon_0 [\cfrac{A_1 K_1 K_2}{d_1 K_2 + d_2 K_1} + \cfrac{A_2 K_1 K_3}{d_1 K_3 + d_2 K_1}]$
Approach 2: Now let’s work out the effective capacitance from the basics
$C_{eq} = \cfrac{Q}{V}$ $=\cfrac{Q_1 + Q_2}{V}$, where $Q_1$ is the magnitude of charge on part of the capacitor plates with dielectric of dielectric strength $K_1$ & $K_2$ sandwiched between them, $Q_2$ is the magnitude of charge on part of the capacitor plates with dielectric of dielectric strength $K_1$ & $K_3$ sandwiched between them, and $V$ is the potential difference between two plates
Rest of the steps are similar to what we did in previous scenario (and if you need help, feel free to ping us).
Parallel plate capacitor with triangular dielectric slab
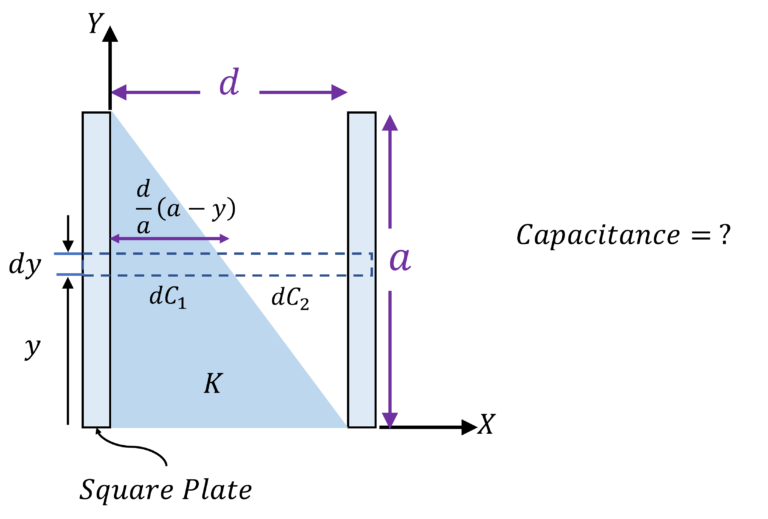
Here note that the charge is not uniformly distributed on the plate. So we will need to think of these capacitor plates as large number of capacitor plates of small area connected to each other in parallel
So, let’s consider a differential element of area $ady$ as shown (Note that we have assumed the capacitor plates to be square plates of side $a$)
Now, capacitance of this differential element $dC$ would be:
$\cfrac{1}{dC}=\cfrac{1}{dC_1}+\cfrac{1}{dC_2}$
$dC_1 = \cfrac{K \epsilon_0 a dy}{\cfrac{d}{a} (a-y)}$
$dC_2 = \cfrac{\epsilon_0 a dy}{d – \cfrac{d}{a} (a-y)}$
$\implies$ $dC = \cfrac{\epsilon_0 a^2 dy}{d} \cfrac{1}{\cfrac{a}{K} + y (1 – \cfrac{1}{K})}$
$C_{eq} = \int dC = \cfrac{K \epsilon_0 a^2}{d (K-1)} ln K$
Parallel plate capacitor with dielectric slab of varying dielectric strength
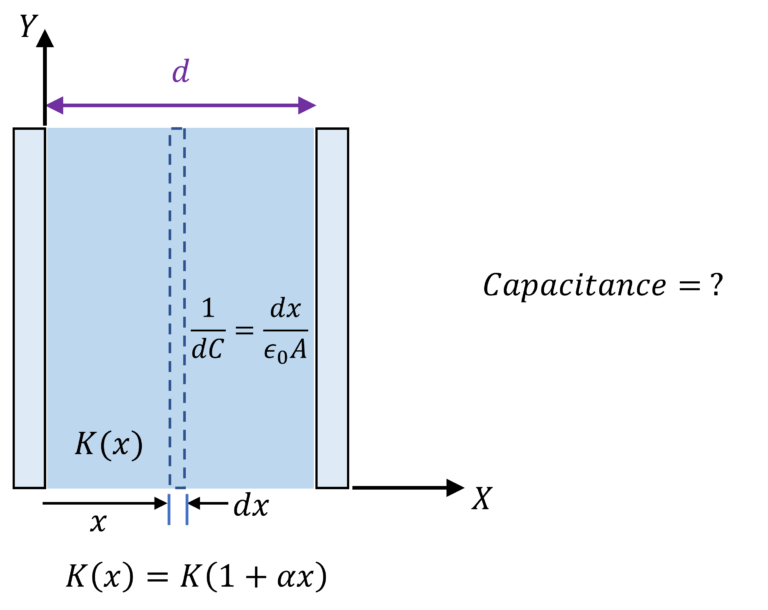
Note that the charge distribution will be uniform across the plates in the given scenario
So $\cfrac{1}{C_{eq}} = \int_0^d \cfrac{1}{dC}$
where $\cfrac{1}{dC} = \cfrac{dx}{K(x)\epsilon_0 A}$
$\implies$ $\cfrac{1}{C_{eq}} = \int_0^d \cfrac{dx}{K(1 + \alpha x) \epsilon_0 A}$ $=\cfrac{1}{K \epsilon_0 A \alpha} ln(1+ \alpha d)$
Or, $C_{eq} = \cfrac{K \epsilon_0 A \alpha}{ln (1 + \alpha d)}$