Five Conducting Parallel Plates

Consider a system of five conducting parallel plates (large plates) of area $A$. The charge on plates $1$, $2$, $3$, $4$ and $5$ is $Q$, $2Q$, $3Q$, $4Q$ and $5Q$ respectively. Initially the two switches are opened. Assume that that distance between the plates, $d$, is very small compared to the dimensions of the plate.

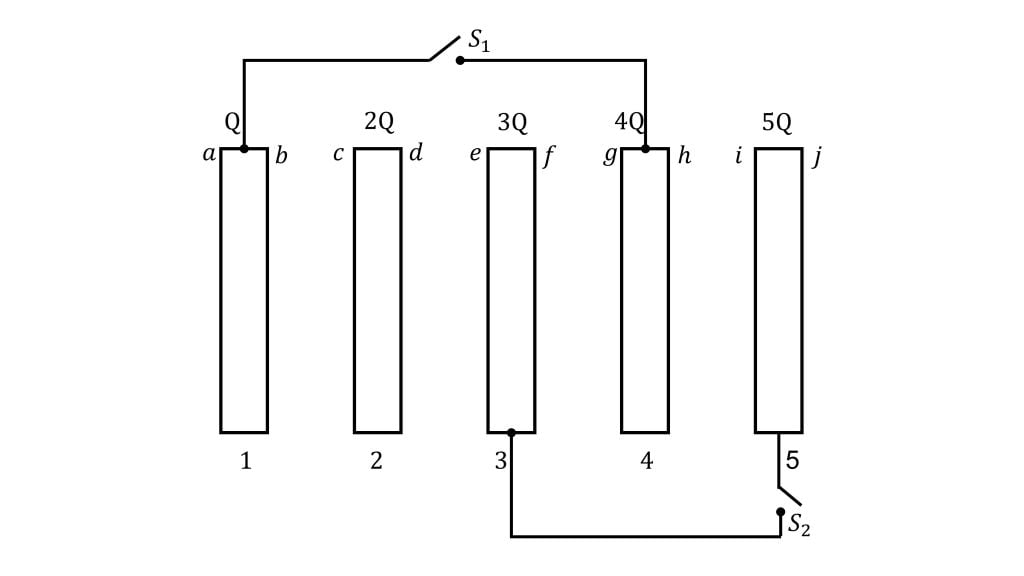
Five Parallel Conducting Plates

So, before switches $S_1$ and $S_2$ are closed, let’s determine
$(1)$ The charge on surface $b$ and
$(2)$ The potential difference between plate $2$ and $3$, i.e. $V_2 – V_3$

So let’s begin with finding the charge on surface $b$ and assume that the charge densities on respective surfaces are as shown 

Five Parallel Conducting Plates - charge on surface b

Two governing principles are: 
(i) Electric field inside all the metallic plates should be zero
(ii) Net charge on the plates (excess + induced) should be equal to the excess charge as stated in the problem statement

So, electric field inside plate $1$ should be zero implies
$\sigma_a = \sigma_b + \sigma_c + \sigma_d + \sigma_e + \sigma_f +\sigma_g + \sigma_h + \sigma_i + \sigma_j$ $\cdots$ (1)

electric field inside plate $2$ should be zero gives us
$\sigma_a + \sigma_b + \sigma_c = \sigma_d + \sigma_e + \sigma_f +\sigma_g + \sigma_h + \sigma_i + \sigma_j$ $\cdots$ (2)

electric field inside plate $3$ should be zero gives us
$\sigma_a + \sigma_b + \sigma_c + \sigma_d + \sigma_e = \sigma_f +\sigma_g + \sigma_h + \sigma_i + \sigma_j$ $\cdots$ (3)

electric field inside plate $4$ should be zero gives us
$\sigma_a + \sigma_b + \sigma_c + \sigma_d + \sigma_e + \sigma_f +\sigma_g = \sigma_h + \sigma_i + \sigma_j$ $\cdots$ (4)

electric field inside plate $5$ should be zero gives us
$\sigma_a + \sigma_b + \sigma_c + \sigma_d + \sigma_e + \sigma_f +\sigma_g + \sigma_h + \sigma_i = \sigma_j$ $\cdots$ (5)

And conservation of charge would give us
$\sigma_a + \sigma_b = \cfrac{Q}{A}$ $\cdots$ (6)
$\sigma_c + \sigma_d = \cfrac{2Q}{A}$ $\cdots$ (7)
$\sigma_e + \sigma_f = \cfrac{3Q}{A}$ $\cdots$ (8)
$\sigma_g + \sigma_h = \cfrac{4Q}{A}$ $\cdots$ (9)
$\sigma_i + \sigma_j = \cfrac{5Q}{A}$ $\cdots$ (10)

Adding (1) and (5), we get $\sigma_a = \sigma_j$

Subtracting (2) from (1) we get $\sigma_b = – \sigma_c$

Subtracting (3) from (2) we get $\sigma_d = – \sigma_e$

Subtracting (4) from (3) we get $\sigma_f = – \sigma_g$

Subtracting (5) from (4) we get $\sigma_h = – \sigma_i$

Now to find surface charge density (or total charge) on surface ‘$b$’, equations (1) and (7) to (10) give us 

$\sigma_a – \sigma_b = \cfrac{14Q}{A}$ $\cdots$ (11)

From (6) and (11) we get
$\sigma_a = \cfrac{7.5Q}{A}$
or $Q_a = 7.5Q$
$Q_b = -6.5Q$
$Q_c = 6.5Q$
$Q_d = -4.5Q$
$Q_e = 4.5Q$
$Q_f = -1.5Q$
$Q_g = 1.5Q$
$Q_h = 2.5Q$
$Q_i = -2.5Q$
$Q_j = 7.5Q$

Note $Q_a = Q_b$

Five Parallel Conducting Plates - charge on all surfaces

Potential difference between plates (2) and (3) would be:
$V_2 – V_3 = – \int \overrightarrow{E}.\overrightarrow{dl}$ $= – \cfrac{\sigma_e}{\epsilon_0}$ $= – \cfrac{4.5Q}{\epsilon_0 A}$

Now assume that both the switches $S_1$ and $S_2$ are closed simultaneously, and determine
$(3)$ The charge on surface $b$ and
$(4)$ The charge on surface $f$.

Five Parallel Conducting Plates - switches closed

Equations (1) through (5) hold true in this scenario as well, which means, that 
$\sigma_a = \sigma_j$
$\sigma_b = -\sigma_c$
$\sigma_d = -\sigma_e$
$\sigma_f = -\sigma_g$
$\sigma_h = -\sigma_i$

Now, total excess charge on plates 1 + 4 $=5Q$
& total excess charge on plates 3 + 5 $=8Q$

So, $\sigma_a + \sigma_b + \sigma_g + \sigma_h = \cfrac{5Q}{A}$
$\sigma_c + \sigma_d = \cfrac{2Q}{A}$
$\sigma_e + \sigma_f + \sigma_i + \sigma_j = \cfrac{8Q}{A}$

Moreover, potential difference between plates 1 and 4 is zero and potential difference between 3 and 5 is zero, which means 
$\sigma_b + \sigma_d + \sigma_f = 0$
& $\sigma_f + \sigma_h = 0$

Solving we get $\sigma_a = \cfrac{7.5Q}{A}$
and $\sigma_f = \cfrac{3}{5} \cfrac{Q}{A}$