Q1 A string of length $L$ and mass $M$ hangs freely from a fixed point. Calculate the velocity of the transverse wave travelling along the string, at a point which is at a distance $x$ from the bottom of the string.
$v = \sqrt{gx}$
Q2 A source of sound of frequency $256 \ Hz$ is moving rapidly towards a wall with a velocity of $5 \ m/s$. How many beats per second will be heard if sound travels at a speed of $330 \ m/s$ and the source is between the wall and the observer?
$8$
Q3 Standing waves are produced by the superposition of two waves:
$y_1 = 0.05 \sin (3 \pi t – 0.5 \pi x)$ and $y_2 = 0.05 \sin (3 \pi t + 0.5 \pi x)$, where $x$ and $y$ are measured in meter and $t$ in second. Find the amplitude of the particle located at $x = 0.5 \ m$.
$\cfrac{01}{\sqrt{2}} \ m$
Q4 A standing wave set up in a medium is given by $y = 4 \cos \left(\cfrac{\pi x}{3}\right) \sin 40 \pi t$ where $x$ and $y$ are in $cm$ and $t$ is in seconds,
(a) What are the amplitude and velocity of the two component waves which produce this standing wave?
(b) What is the distance between the adjacent nodes?
(c) What is the velocity of the particle of the medium at $x = 3 \ cm$ at time $t = \cfrac{1}{8} \ sec$?
(a) $2 \ cm, \ 120 \ m/s$
(b) $3 \ cm$
(c) $160 \pi \ cm/sec$
Q5 A $2 \ m$ long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is $200 \ m/s$ and the amplitude of standing wave is $0.5 \ cm$.
(a) Find the wavelength and the frequency
(b) Write the equation giving the displacement of different points as a function of time. Choose the $X$-axis along the string with the origin at one end and $t = 0$ at the instant when the point $x = 50 \ cm$ reached its maximum displacement.
(a) $2 \ m, \ 100 \ Hz$;
(b) $(0.5 \ cm)$ $\sin$$ [(\pi m^{-1})x]$ $\cos$$ [(200 \ \pi s^{-1})t]$
Q6 A bus is moving towards a huge wall with a velocity of $5 \ m/s$. The driver sounds a horn of frequency $200 \ Hz$. The frequency of the beats heard by a passenger of the bus will be (in $Hz$) nearly ( velocity of sound in air $ = 338 \ m/s$)
$6$
Q7 A string is stretched along the $X$ axis. A disturbance given by the equation $y(x, t) = 4 \sin \left(\cfrac{\pi x}{3}\right) \cos (10 \pi t)$, is produced in the string. Where $X$ is in $cm$ and $t$ is in seconds. If the Distance between two adjacent nodes is $n \ cm$, then find the value of $n$.
$3$
Q8 When two progressive waves $y_1 = 4 \sin (2x – 6 t)$ and $y_2 = 4 \sin \left(2x – 6t – \cfrac{2 \pi}{3}\right)$ are superimposed, find the amplitude of the resultant wave.
$4$
Q9 The fundamental frequency of a sonometer wire increases by $6 \ Hz$ if its tension is increased by $44$% keeping the length constant. What will be the change in the fundamental frequency when length of wire is increased by $20$% keeping the original tension in the wire.
$5$
Q10 An open pipe is suddenly closed at one end, as a result of which the frequency of third harmonic of the closed pipe is found to be $100 \ Hz$ higher than the fundamental frequency of the open pipe. If fundamental frequency of the open pipe is $400/n \ Hz$. Find the value of $n$.
$2$
Q11 A simple harmonic wave has the equation $y = 0.5 \sin (314 t – 1.57 x)$, where $y, \ x$ are in meters and $t$ is in seconds.
(a) Find the frequency and the wavelength of this wave.
(b) Another wave has the equation $y’ = 0.1 \sin (314 t – 1.57 x + 1.57)$. Deduce the Phase difference between them and the ratio of their intensities.
(a) $50 \ Hz, \ 4 \ m$
(b) $\pi/2, \ 25$
Q12 The water level in a vertical glass tube $1 \ m$ long can be adjusted to any position in the tube. A tuning fork vibrating at $686 \ Hz$ is held just over the open top end of the tube. At what positions the water level will there be resonance? ( velocity of sound $ = 330 \ m/s$)
$12 \ cm, \ 36 \ cm, \ 60 \ cm, \ 84 \ cm$
Q13 A tuning fork $P$ of unknown frequency gives $7$ beats in $2$ second with another tuning fork $Q$. When $Q$ is moved rightward towards a wall with speed $5 \ m/s$, it gives $5$ beats per Second for a stationary observer located left to it. On filing, $P$ gives $6$ beats per second with $Q$. What is the frequency of $P$? [Speed of sound $ = 332 \ m/s$].
$169.5 \ Hz$
Q14 A steel wire is rigidly fixed at both ends. Its length, mass and cross-sectional area are $1 \ m, \ 0.1 \ kg$ and $10^{-8} \ m^2$ respectively. Tension in the wire is produced by lowering the temperature by $20^{\circ}C$. If transverse waves are set up by plucking the wire at $0.25 \ m$ from one end, and assuming that the wire vibrates with minimum number of loops possible for such a case. The frequency of vibration (in $Hz$) is found to be $11K$. Find the value of $K$. Given $\alpha = 1.21 \times 10^{-5} \ {^{\circ}C^{-1}}, \ Y = 2 \times 10^{11} \ N/m^2$.
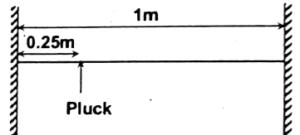
$2$
Q15 A point like sound source emits sound in all direction uniformly. An observer who is at a distance of $50 \ m$ from the source detects sound of intensity $10^{-5} \ watt/m^2$. If the bulk modulus of air is $1.6 \times 10^5 \ N/m^2$ and velocity of sound is $340 \ m/a$. Find power developed by sound source and pressure amplitude at the position of observer.
$3.14 \times 10^{-4} \ Watt, \ 3.07 \times 10%{-3} \ N/m^2$
Q16 Acceleration of point $x = 2 \ m$ of a transverse wave is $5 \hat{j} \ m/s^2$ and the slope of waveform is given by $\cfrac{dy}{dx} = 5 \sin \cfrac{\pi}{12}x$. Then the speed of the point at that instant is given in $m/s$ as
$\sqrt{\cfrac{150}{\pi \sqrt{3}}}$
Q17 The speed of sound in air is $332 \ m/s$ at NTP. What will be the speed of sound in hydrogen at NTP if the density of hydrogen at NTP is $1/16$ that of air $[$assume $P_H = P_{\text{air}}]$?
$1328 \ m/s$
Q18 Two wires made up of same material and having same length and radii $r$ and $2r$, respectively, are welded together end to end. This combination is used as a sonometer wire, kept under tension $T$. The welded point is midway between the two bridges. What would be the ratio of the number of loops formed in the wires such that the joint is a node when stationary vibrations are set up in the wires.
$n_r : n_{2r} = 1 : 2$
Q19 Two tuning forks $A$ and $B$ give three beats per second. A resonates with a closed column of air $30 \ cm$ long and $B$ with an open column $71 \ cm$ long, both in their fundamental modes. Calculate the frequencies of the tuning forks.
$19.32 \ Hz, \ 16.32 \ Hz$
Q20 A transverse wave is travelling along a string from left to right. Adjoining figure represents the snapshot at a given instant. At this instant,
(a) which of the points will have an upward velocity?
(b) which of the points will have downward velocity?
(c) which of the points have zero velocity?
(d) which of the points have maximum magnitude of velocity ?
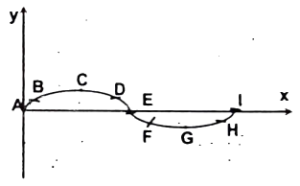
(a) $D, E, F$;
(b) $A, B, H, I$;
(c) $C, G$;
(d) $A, E, I$
Q21 A person standing between two parallel hills fires a gun. He hears the first echo after $1.5 \ sec$ and the second after $2.5 \ sec$. If the speed of sound in air is $332 \ m/s$. Then find the time (in $sec$) when he hear the third echo?
$4$
Q22 Two identical flutes produces fundamental notes of frequency $300 \ Hz$ at $27^{\circ}C$. If the temperature of the air in one flute is increased to $31^{\circ}C$. Find the number of beats (approx.) heard per second.
$2$
Q23 A tuning fork produces first resonance in a glass tube containing an air column when the length of the air column was $44 \ cm$ and again when length was $140 \ cm$ in the same tube. Calculate the end correction in $cm$.
$4$
Q24 A closed organ pipe and an open pipe of the same length produce $4$ beats when they are set into vibrations simultaneously. If the length of each of them were twice their initial lengths, then find the number of beats produced.
$2$




