Center of Mass of Semicircular and Annular Semicircular Disc(s)

Here is the center of mass of a semicircular and annular semicircular disc.

Center of Mass of Semicircular Disc

Moment of Inertia of Semicircular Disc
Moment of Inertia of Semicircular Disc

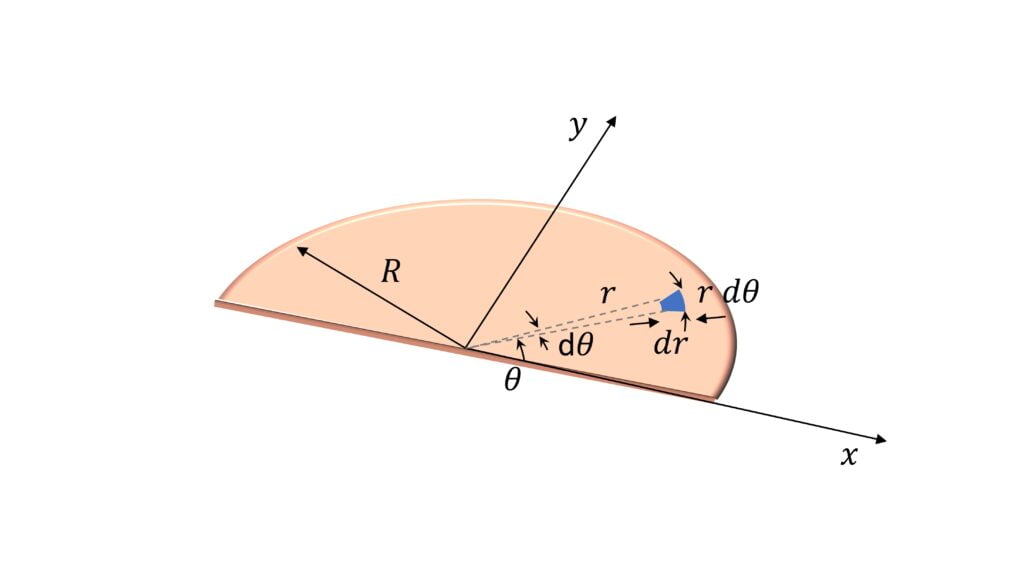
$x_{cm} = 0$
$y_{cm} = \cfrac{4R}{3 \pi}$

Approach 1: Use the expression derived for uniform circular arc (disc), where we found that $y_{cm} = \cfrac{2}{3} R \cfrac{\sin (\alpha /2)}{(\alpha /2)}$

Approach 2:
$y_{cm} = \cfrac{\int ydm}{\int dm}$
$y = r \sin \theta$
$dm = \sigma r dr d \theta$

$\implies$ $y_{cm} = \cfrac{\sigma \int_0^R r^2 dr \int_0^{\pi} \sin \theta d \theta}{\sigma \int_0^R r dr \int_0^{\pi} d \theta}$
$=\cfrac{4R}{3 \pi}$

Center of Mass of Annular Semicircular Disc

Moment of inertia of annular semicircular disc
Moment of inertia of annular semicircular disc

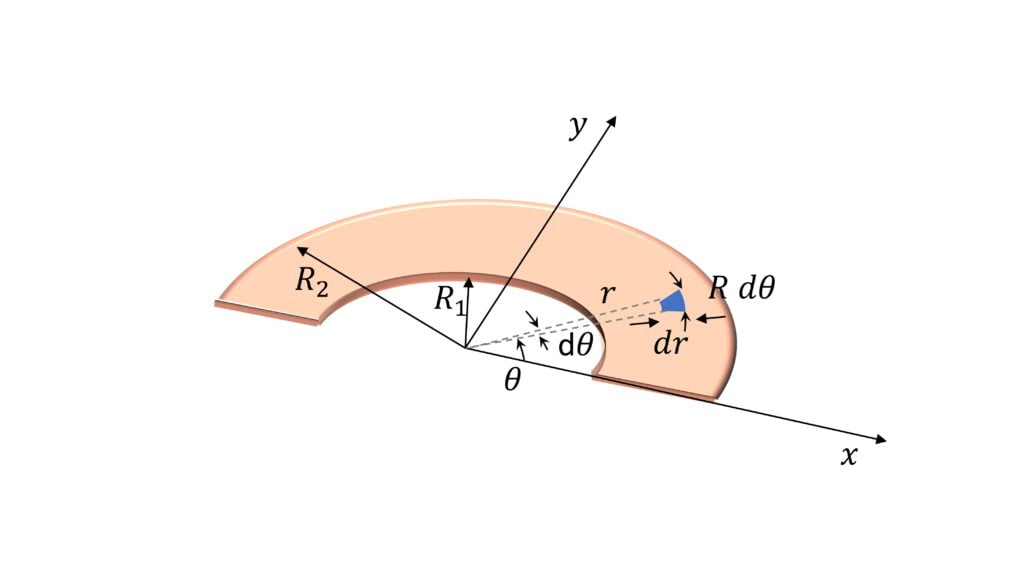
$x_{cm}=0$
$y_{cm} = \cfrac{4}{3 \pi} \cfrac{R_1^2 + R_1 R_2 + R_2^2}{R_1+R_2}$

$y_{cm} = \cfrac{\int ydm}{\int dm}$
$y = r \sin \theta$
$dm = \sigma r dr d \theta$

$\implies$ $y_{cm} = \cfrac{\sigma \int_0^R r^2 dr \int_0^{\pi} \sin \theta d \theta}{\sigma \int_0^R r dr \int_0^{\pi} d \theta}$
$=\cfrac{4}{3 \pi} \cfrac{R_1^2 + R_1 R_2 + R_2^2}{R_1+R_2}$

To continue to explore center of mass of other commonly encountered shapes, click here…

JEE Physics Online Classes