Center of Mass of Solid and Hollow Hemisphere’s

Here is the center of a solid hemisphere and that of a hollow hemisphere

Center of Mass of Solid Hemisphere

Moment of inertia of solid hemisphere
Moment of inertia of solid hemisphere

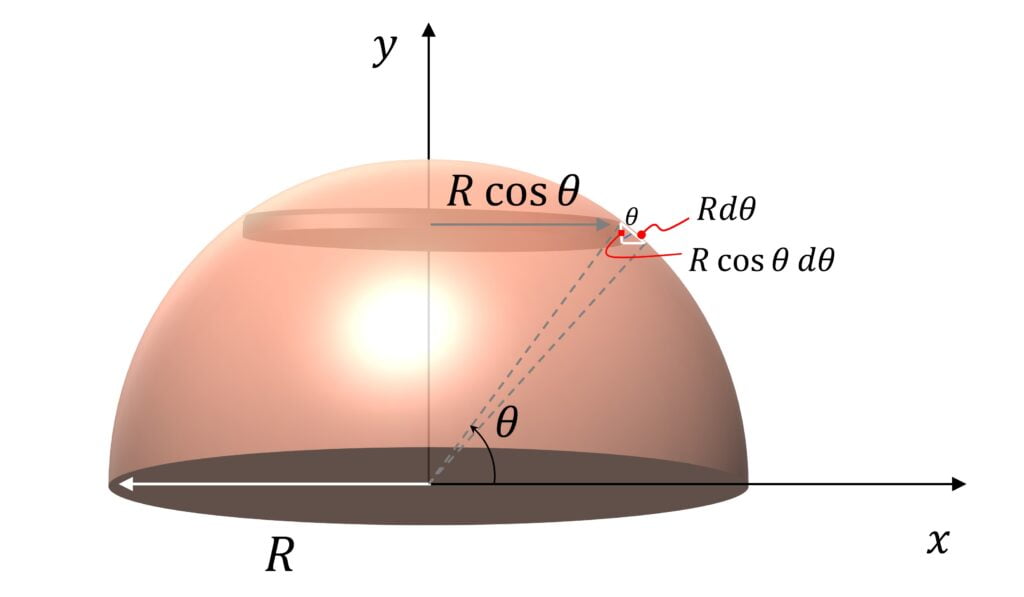
$x_{cm} = 0$
$y_{cm} = \cfrac{3R}{8}$

$x_{cm} = 0$ because of symmetry about $y-$axis

$y_{cm} = \cfrac{\int ydm}{\int dm}$

$dm = \pi (R \cos \theta)^2 (R \cos \theta) d \theta$ $=\pi R^3 \cos^3 \theta d \theta$
$y = R \sin \theta$
So,
$y_{cm} = R\cfrac{\int_0^{\pi/2} \sin \theta \cos^3 \theta d \theta}{\int_0^{\pi/2} \cos^3 \theta d \theta}$

Solving we get $y_{cm} = \cfrac{3R}{8}$

Center of Mass of Hollow Hemisphere

Moment of inertia of hollow hemisphere
Moment of inertia of hollow hemisphere

$y_{cm} = \cfrac{3}{8} \cfrac{(R_2^2 + R_1^2)(R_1 + R_2)}{R_2^2 +R_1 R_2 + R_1^2}$

$(m_1 + m_2) \cfrac{3R_2}{8} = m_2 y_{cm} + m_1 \cfrac{3R_1}{8}$

$m_1 = \cfrac{4}{3} \pi R_1^3 \rho$

$m_2 = \cfrac{4}{3} \pi (R_2^3 – R_1^3) \rho$

Solving we get
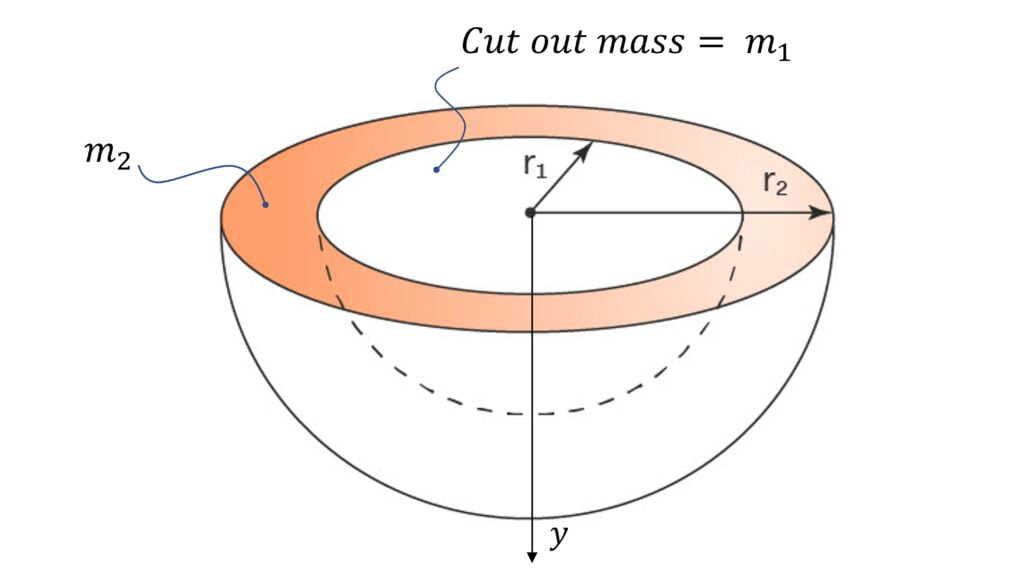
$y_{cm} = \cfrac{3}{8} \cfrac{(R_2^2 + R_1^2)(R_1 + R_2)}{R_2^2 +R_1 R_2 + R_1^2}$

To continue to explore center of mass of other commonly encountered shapes, click here…

JEE Physics Online Classes