In JEE Main paper, you can expect up to 2 questions from ‘Kinematics’ while in JEE Advanced (IIT JEE) you can expect up to 1 question. It is generally considered to be a scoring topic, if you can master the different types questions that have been or could be asked in JEE Main and JEE Advanced papers on Kinematics. So here in this blog, we would examine all different types of questions asked on this topic and will highlight the Important Questions of Kinematics Class 11 topic.
A rating of 5 stars means that you should have that question mastered, so make sure that you practice similar questions on AceJEE platform and do listen to the explanation video on that question type by Vikas Sir where he covers all the basics, step by step approach along with a solved problem from latest JEE Main / Advanced papers. A rating of 3 stars means that there is a good chance that questions might be asked on that question type as well based on previous 3 year question papers and a rating of 1 means we have not seen the focus on that question type in last 3 to 5 years but that does not mean that you should ignore that question type as examiners do tend to move around between the question types.
So let’s begin with a quick overview of one dimensional motion
Kinematics | One Dimensional Motion

For a body moving along one dimension, say $x$,
- it’s displacement $\Delta x$ is defined as final position minus initial position i.e. $x_f – $ $x_i$ which may be positive or may be negative and may or may not be equal to the distance travelled in going from $x_i$ to $x_f$
- it’s average speed is defined as $=\cfrac{Total \ Distance}{Time \ Duration}$ or distance travelled in 1 sec and may or may NOT be same as average velocity ($\cfrac{Net \ Displacement}{Time \ Duration}$)
- it’s instantaneous velocity is $\cfrac{ds}{dt}$, i.e. small displacement $ds$ in small time duration $dt$ at time $t$. Note instantaneous speed = magnitude of instantaneous velocity
- it’s two independent equations of motion for constant acceleration are given by $v =$ $u +$ $at$, $\Delta x =$ $ut+$ $\cfrac{1}{2} at^2$, where you have 5 variables $u$, $v$, $\Delta x$, $a$, and $t$, which means you can only solve for 2 unknown variables or you must be given information on other 3 variables.
- Alternate form of above equations are $v^2 =$ $u^2 +$ $2a \Delta x$, no $t$ involved here (more commonly used), $\Delta x =$ $vt -$ $\cfrac{1}{2} at^2$, no $u$ involved here and $\Delta x =$ $(\cfrac{v+u}{2})t$
Now let’s take a look at different types of questions asked in JEE Main and JEE Advanced on one dimensional motion
Important Questions | One Dimensional Motion
In JEE Advanced we have not seen many questions over last 5 to 10 years but in JEE Mains 2020 and 2021, we saw an equal spread of questions between 1D (one dimensional) Motion and 2D (two dimensional) Motion (including vectors)
So here we will look at questions involving variable acceleration and questions involving constant acceleration
Variable Acceleration
There are 5 different types of questions you can expect in JEE Main or JEE Advanced on 1D Motion involving variable acceleration
Questions Type 1/40: Given position $x(t)$ or velocity $v(t)$ or acceleration, $a(t)$ of a particle, you will be asked to determine information about the other two kinematic variables. For example,

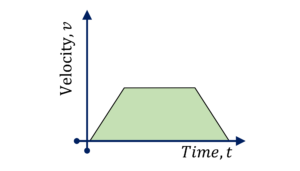
Question Type 2/40: Given information on speed, $v$, vs time, $t$ graph, you will be asked to determine some information about particle’s position or acceleration (average or instantaneous). For example,
Question Type 3/40: Given acceleration $a$ as a function of time $t$, determine speed, $v$ as a function of time $t$ and further you might be asked to determine parameters such as maximum speed in the given time duration. For example,

Question Type 4/40: Given acceleration $a$, as a function of position, $x$, determine velocity $v$ as a function of position $x$. For example,
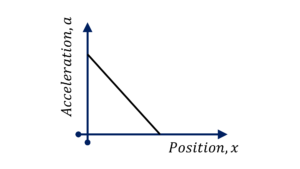
Question Type 5/40: Given acceleration $a$ of a particle as a function of its velocity $v$, determine the velocity or position of the particle at some time $t$. For example,

Constant Acceleration
Questions on 1D Motion with particle under constant acceleration can be divided into the following 4 question types.
Question Type 6/40: Simpler application | For a particle under constant acceleration, determine the unknown using two independent kinematic equations $v=$ $u+$ $at$, $x=$ $ut+$ $\cfrac{1}{2} a t^2$. For example,
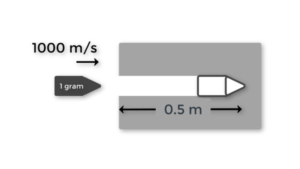
Question Type 7/40: 1D Motion with constant acceleration without change in direction of motion. Here the information on 3 of the 5 kinematic variables ($v$, $u$, $a$, $t$ and displacement $s$) is given at three points along the particle’s path (instead of initial and final points only). Use $v=$ $u+$ $at$, $x=$ $ut+$ $\cfrac{1}{2} a t^2$. Note that sometimes $v^2 +$ $u^2 +$ $2as$, comes in handy when information is not given on time $t$. For example,
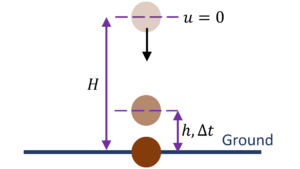
Question Type 8/40: 1D Motion with constant acceleration but particle’s initial velocity is in opposite direction to its acceleration which means that the particle would undergo change in direction during its motion. In such situations, the distance and displacement will not be equal if the time duration of interest includes the moment when particle changes direction. Here you might be given position $x$ as an algebraic function of time $t$ ($x=A +$ $Bt + Ct^2$ – constant acceleration) and you might be asked to determine the distance traveled. In such questions check for signs of velocity and acceleration at time $t = 0$ and if the signs are opposite, note that displacement will not be same as distance, if the particle has zero velocity at some time $t$ in the duration of interest. For example,

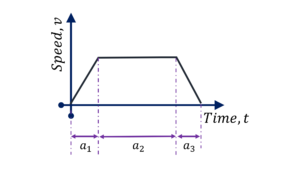
Question Type 9/40: 1D Motion with different acceleration for different segments of the journey. Here you need to make sure that you write your kinematic equations for constant acceleration, $v=$ $u+$ $at$, $x=$ $ut+$ $\cfrac{1}{2} a t^2$, separately for the two segments and then solve for the unknown. For example,
Vectors

Vectors are physical quantities which have a magnitude as well as a direction and they obey laws of vector algebra. Please refer to the lecture video for detailed understanding of vectors. But make sure that you are comfortable with graphical representation and treatment of vectors as well as treatment of vectors in unit vector notation ($\overrightarrow{a} =$ $a_x \hat{i} +$ $a_y \hat{j} +$ $a_z \hat{k}$).
And note that vectors can be multiplied in two different ways, a scalar/dot product or a cross/vector product
Scalar/Dot product: $\overrightarrow{A}.\overrightarrow{B}=$ $AB \cos \theta=$ $A_x B_x+$ $A_y B_y+$ $A_z B_z$
Vector/Cross Product: $\overrightarrow{A} \times \overrightarrow{B}=$ $AB \sin \theta \hat{n}=$ $(A_y B_z – A_z B_y)$ $\hat{i}-$ $(A_x B_z – A_z B_x)$ $\hat{j}+$ $(A_x B_y – A_y B_x)$ $\hat{k}$
Now let’s take a look at different types of questions asked in JEE Main and JEE Advanced on vectors.
Important Questions of Kinematics Class 11 | Vectors
Question Type 10/40: Given coordinates of two points, find the vector joining those two points. For example,
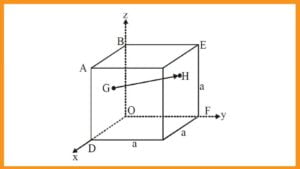
Question Type 11/40: Find angle between two vectors given some relation between the two vectors. Here the two vector algebra operations that come in handy are (1) $\overrightarrow{A}.\overrightarrow{B}=$ $AB \cos \theta$ (2) $|\overrightarrow{A}+\overrightarrow{B}|^2=$ $(\overrightarrow{A}+\overrightarrow{B}).(\overrightarrow{A}+\overrightarrow{B})$
For example,

Question Type 12/40: Questions involving use of vector algebra with vectors either given in unit vector notation or in graphical representation. For example,
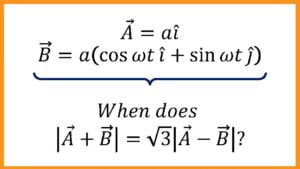
Two Dimensional Motion
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Kinematics Class 11 Important Questions | Two Dimensional Motion
Question Type 13/40: For a particle moving along $x$ and $y$, given $x(t)$ and $y(t)$ i.e. given $x$ and $y$ as a function of time $t$, determine it’s velocity or acceleration vector at some time $t$ or determine it’s trajectory (which is nothing but equation relating $x$ and $y$, without $t$ in it). For example,

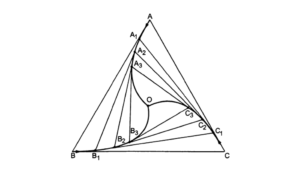
Question Type 14/40: For a group of particles that are symmetrically placed and moving towards each other at constant speed, determine the time it will taken for them to meet/collide. For example,
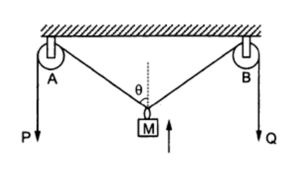
Question Type 15/40: Establish motion of connected objects. For example,
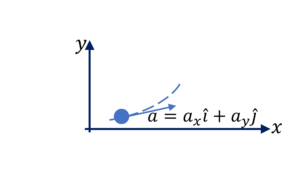
Question Type 16/40: Given that a particle is under constant acceleration with the 2D/3D acceleration vector given in unit vector notation $\overrightarrow{a}=$ $a_x \hat{i} +$ $a_y \hat{j} +$ $a_z \hat{k}$, determine velocity vector, $\overrightarrow{v}$ or position vector $\overrightarrow{r}$ at time $t$. For example:
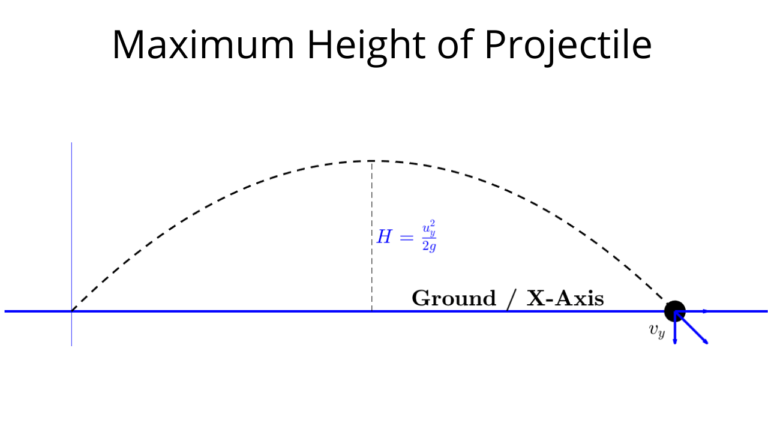
Projectile Motion (Sign up for Free for question types on projectile motion)
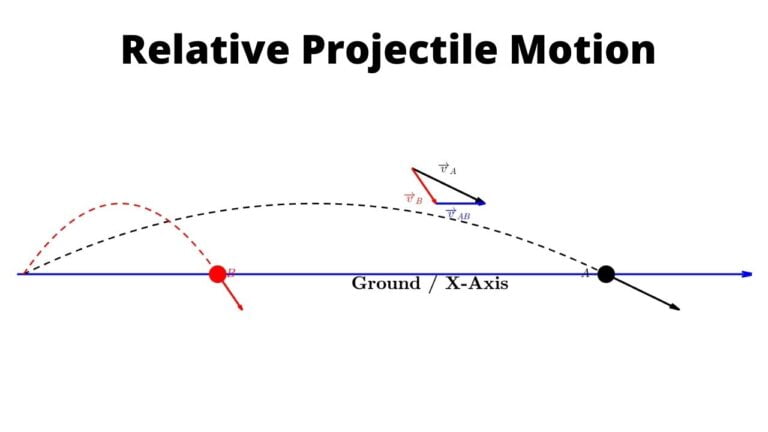
Relative Velocity (Sign up for Free for question types on relative velocity)