Maximum height of projectile thrown from ground is given by $\cfrac{u^2 \sin^2 \theta}{2g}$ and if the projectile is projected from a height $H$, then the maximum height attained by projectile during it’s flight is $H + \cfrac{u^2 \sin^2 \theta}{2g}$ as measured from the ground
So let’s see how we can quickly derive the maximum height from the equations of motion of a projectile
Maximum Height in Projectile Motion
Maximum height of a projectile, i.e., the maximum displacement in the y -direction is governed only by the kinematic equations in y – direction i.e. $v_y =$ $u_y -$ $gt$ & $y =$ $ut -$ $\cfrac{1}{2} gt^2$ or $v_y^2 = u_y^2 – 2gy$
Now, what is the vertical component of velocity or speed in vertical direction at maximum height? Well, it is zero at that point i.e. $v_y = 0$ at maximum height
So $0 = u_y^2 – 2gH$ or $H = \cfrac{u_y^2}{2g}$ $=\cfrac{u^2 \sin^2 \theta}{2g}$
The horizontal range and maximum height of a projectile are equal - When?
Maximum height of a projectile, $H$ $=\cfrac{u^2 \sin^2 \theta}{2g}$, where once again $u$ is the initial speed, $\theta$ is the angle of projection, and $g$ is the acceleration due to gravity
Horizontal Range of a projectile, $R$ $=\cfrac{2u^2 \ sin \theta \cos \theta}{g}$
$H=R$ when $\cfrac{u^2 \sin^2 \theta}{2g}$ $=\cfrac{2u^2 \ sin \theta \cos \theta}{g}$
or when, $\tan \theta = 4$ or when the angle of projection, $\theta =$ $\tan^{-1} 4$
With that, now let’s explore the trajectory of a projectile, i.e. establish expression $y = f(x)$ for the path traced by the projectile
Projectile Motion | Important Questions | JEE PYQs
- Types of projectile motion
- Equations of projectile motion
- Range of a projectile
- Maximum height of a projectile
- Trajectory of a projectile
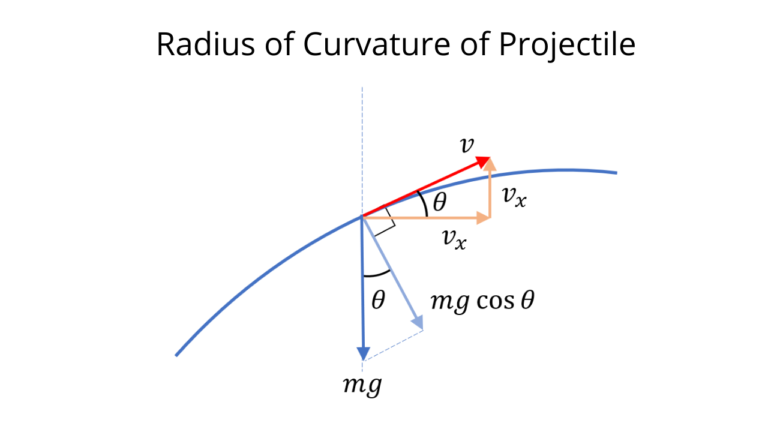
- Radius of curvature of projectile
- Velocity of projectile at time $t$ or height $h$
- Projectile Motion Examples
- Projectile motion along an inclined plane
- Relative motion of projectile(s)
Kinematics Overview – What you need to know for JEE Main and JEE Advanced