(Physics) Kinematics DPP | Daily Practice Problems ( 2 / 12)
Q1. Two vectors have magnitudes 3 unit and 4 unit respectively. What should be the angle between them if the magnitude of the resultant is
a) 1 unit
b) 5 unit and
c) 7 unit
Answer
Correct answer is (a) $180^\circ$ (b) $90^\circ$ (c) $0^\circ$
Q2. Establish the following vector inequalities geometrically or otherwise:
a) |$\overrightarrow{a}$ + $\overrightarrow{b}$| $\leq$ $\overrightarrow{a}$| + |$\overrightarrow{b}$|
b) |$\overrightarrow{a}$ + $\overrightarrow{b}$| $\geq$ $\overrightarrow{a}$| – |$\overrightarrow{b}$|
Answer
The sum (difference) of any two sides of a triangle is never less (greater) than the third side
Q3. If the vectors $2 \hat{i} + 3 \hat{j} + c \hat{k}$ and $-3 \hat{i} + 6 \hat{k}$, the value of $c$ is
Answer
Correct answer is 1
Q4. In the given figure, two numerically equal forces are acting at a point A. Find the magnitude of the resultant force.
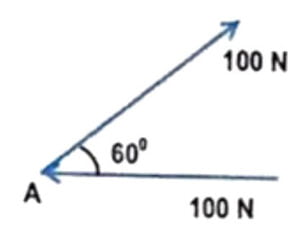
Answer
Correct answer is 100 N
Q5. Three forces $\overrightarrow{F_1}$, $\overrightarrow{F_2}$ and $\overrightarrow{F_3}$ are acting on a particle such that the particle remains in equilibrium. If $\overrightarrow{F_1}=$ $(2 \hat{i} + 3 \hat{j})$ N and $\overrightarrow{F_2}=$ $(2 \hat{j} + 2 \hat{k})$ N, find $\overrightarrow{F_3}$
Answer
Correct answer is $\overrightarrow{F}_3=-(2 \hat{i} + 5 \hat{j} + 2\hat{k})$ N
Q6. Prove that the vectors $\overrightarrow{A}=$ $ 3\hat{i} + 2\hat{j} -2 \hat{k}$, $\overrightarrow{B}=$ $ -\hat{i} +3 \hat{j} +4 \hat{k}$ and $\overrightarrow{C}=$ $4 \hat{i} – \hat{j} -6 \hat{k}$ can form a triangle.
Answer
$\overrightarrow{A}-\overrightarrow{B}+\overrightarrow{C}=0$
Q7. If $\overrightarrow{a}$ + $\overrightarrow{b}$ = $\overrightarrow{c}$ and a + b = c. What is the angle between $\overrightarrow{a}$ and $\overrightarrow{b}$
Answer
Correct answer is $0^\circ$
Q8. If $\overrightarrow{P}$ $= m\hat{i} -2 \hat{j} +2 \hat{k}$ and $\overrightarrow{}$ $=2 \hat{i} -n \hat{j} + \hat{k}$ are parallel to each other, then find m and n.
Answer
Correct answer is m = 4, n = 1
Q9. If $\alpha$, $\beta$, and $\gamma$ are the angles made by an vector with x, y, and z axes respectively, then find the value of $\cos^2 \alpha + $\cos^2 \beta – \sin^2 \gamma$.
Answer
Correct answer is zero
Q10. A football is kicked vertically upward from the ground, and a student gazing out of the window sees it moving upwards past hear at 5.00 m/s. The window is 15.0m above the ground, Air resistance may be ignored
(a) How high does the football go above the ground?
(b) How much time does it take to go from the ground to its highest point? Take g = 10 $m/s^2$
Answer
Correct answer is (a) 16.25 m (b) 1.8 sec
Q11. A projectile takes off with an initial velocity of 10 takes off with an initial velocity of 10 m/s at an angle of elevation of $45^\circ$. It is just able to clear two hurdles of height 2m each, separated from each other by a distance d. Calculate d. At what distance from the point of projection is the first hurdle placed? Take g = 10 $m/s^2$
Answer
Correct answer is 4.5 m, 2.75 m
Q12. The v-s graph for an airplane travelling on a straight run-way is shown. Determine the acceleration of the plane at $s = 50$ m and $s = 150$ m. Draw the $a-s$ graph.
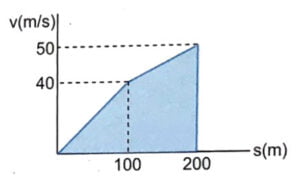
Answer
Correct answer is 8 $m/s^2$, 4.5 $m/s^2$
Q13. A point moving in a straight line traversed half the distance with a velocity $v_0$. The remaining part of the distance was covered with velocity $v_1$ for half the time, and with velocity $v_2$ for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
Answer
Correct answer is $\cfrac{2v_0 (v_1+v_2)}{2v_0+v_1+v_2}$
Q14. At the instant the traffic light turns green, a car starts with a constant acceleration of 2.2 $m/s^2$. At the same instant a truck, travelling with a constant speed of 9.5 m/s, overtakes and passes the car.
(a) How far beyond the starting point will the car overtake the truck?
(b) How fast will the car be travelling at the instant?
Answer
Correct answer is (a) 82 m; (b) 19 m/s
Q15. A train is crossing an observer standing on a platform. The first compartment of the train takes 2 second to cross the observer while the second compartment takes 2.5 seconds to cross him. The train is moving with uniform acceleration. Find : (a) the velocity of the train when the front of the first compartment crosses the observer, and (b) the acceleration of the train. Given, the length of each compartment is 15 meters
Answer
Correct answer is (a) 8.17 m/s (b) -0.67 m/s^2
Q16. (i) A ball is thrown vertically upwards with a speed of 20 m/s from a hard floor. Draw a graph showing the velocity of the ball as a function of time, if the ball suffers elastic collisions continuously.
(ii) Figure shows the x-coordinate of a particle as a function of time. Find the signs of $v_x$ and $a_x$ at $t=t_1$ , $t=t_2$, and $t=t_3$
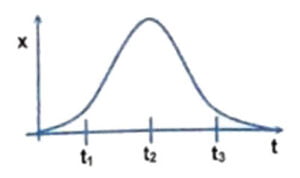
Answer
Correct answer is (ii) $v_x$ is +ve at $t_1$, 0 at $t_2$, -ve at $t_3$, while $a_x$ is +ve at $t_1$, -ve at $t_2$ and +ve at $t_3$
Q17. A projectile is thrown with a velocity $\overrightarrow{v_0}=$ $3 \hat{i} + 4 \hat{j}$ m/s where $\hat{i}$ and $\hat{j}$ are the unit vectors along the horizontal and vertical direction respectively. What is the speed of the projectile at the highest point of its motion?
Answer
Correct answer is 3 m/s
Q18. A particle is thrown over a triangle from one end of a horizontal base and grazing the vertex, it falls on other end of base. If $\alpha$ and $\beta$ are base angles and $\theta$ the angle of projection, prove that $\tan \theta=$ $\tan \alpha +$ $\tan \beta$

Answer
If the coordinates of vertex of the triangle are (x,y), then
$\tan \alpha =$ $\cfrac{y}{x}$; $\tan \beta =$ $\cfrac{y}{R-x}$, where $R$ is the range of the projectile ($\cfrac{u^2 \sin 2\theta}{g}$). $\implies$ $\tan \alpha + \tan \beta = $ $\cfrac{y}{x} \cfrac{R}{R-x}$
Now, $x = u \cos \theta t$; $y = u \sin \theta t – 1/2 g t^2$, where $t$ is the time when projectile is at (x,y)
Substituting the expression for y, x and R in the equation for $\tan \alpha + \tan \beta$, we will get $\tan \theta$ on the right hand side
Q19. A particle is projected from point A perpendicular to inclined plane with a velocity of 50 m/s as shown in the figure. Particle strikes a vertical plane perpendicularly at point B. Find the time taken by particle in going from point A to point B.
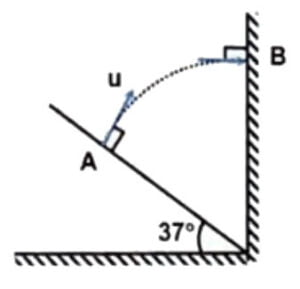
Answer
Correct answer is 4 sec
Q20. A river is flowing with the velocity of $2 \sqrt{3}$ m/s. A boat has to move from A to B. Find the minimum velocity of boat in still water.
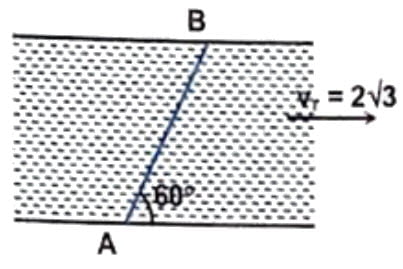
Answer
Correct answer is 3 m/s