From gravitation you can expect 1 question each in JEE Main and JEE Advanced. This topic can be scoring if you can master all different types of questions
Q1 A Saturn year is $29.5$ times the Earth year. How far is the Saturn from the Sun if the Earth is $1.50 \times 10^8 \ km$ away from the Sun ?
Correct answer is $1.43 \times 10^{12} \ m$
Q2 Assuming the Earth to be a sphere of uniform mass density. How much would a body weigh half way down to the center of the Earth if it weighed $250 \ N$ on the surface ?
Correct answer is $125 \ N$
Q3 If the Earth were a perfect sphere of radius $6.37 \times 10^6 \ m$, rotating about its axis with a period of one day $( = 8.64 \times 10^4 \ s)$, how much would the acceleration due to gravity $(g)$ differ from the poles to equator ?
Correct answer is $g_{\text{pole}} – g_{\text{equator}} = 3.37 \times 10^{-2} \ ms^{-2}$
Q4 A rocket is fired vertically with a speed of $5 \ km \ s^{-1}$ from the Earth’s surface. How far from the Earth does the rocket go before returning to the Earth ? Mass of the earth $ = 6.0 \times 10^{24} \ kg$. Mean radius of the Earth $ = 6.4 \times 10^6 \ m; \ G = 6.67 \times 10^{-11} \ N \ m^2 \ kg^{-2}$.
Correct answer is $8.0 \times 10^6 \ m$ from the earth’s center
Q5 The escape speed of a projectile on the Earth’s surface is $11.2 \ km \ s^{-1}$. A body is projected out with thrice this speed. What is the speed of the body far away from the Earth ? Ignore the presence of the Sun and other planets.
Correct answer is $31.7 \ km/s$
Q6 Find the gravitational force of attraction between a particle of mass $m$ and a uniform slender rod of mass $M$ and length $L$ for the two orientations shown in the figure below.
Correct answers are
(a) $\cfrac{GmM}{d(d + L)}$
(b) $\cfrac{2GmM}{d\sqrt{L^2 + 4d^2}} \ \downarrow$
Q7 Two bodies of masses $m_1$ and $m_2$ are connected by a long inextensible cord of length (mass $m_e$), the direction of the cord being always radial as shown in the figure. Find: (a) the tension in the cord and (b) the accelerations of $m_1$ and $m_2$. Does the cord ever become slack ? (ignore the gravitational interaction between $m_1$ and $m_2$)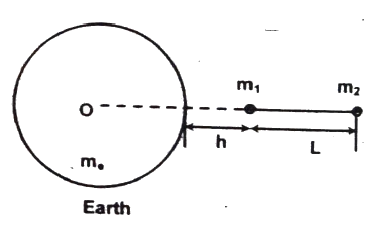
Correct answers are
Tension in the cord $ = \cfrac{Gm_em_1m_2}{m_1 + m_2} \left[\cfrac{1}{(h + R)^2} – \cfrac{1}{(h + R + L)^2}\right]$
Acceleration $a_1 = a_2 = \cfrac{Gm_e}{m_1 + m_2} \left[\cfrac{m_1}{(h + R)^2} + \cfrac{m_2}{(h + R + L)^2}\right]$
towards the center of the earth. The cord will always be in tension.
Q8 A body is thrown up (radially outward from the surface of the earth) with a velocity equal to one-fourth of the escape velocity. Find the maximum height-reached from the surface of the earth. (Radius of earth is $R_e$)
Correct answer is $\cfrac{R_e}{15}$
Q9 A satellite is put in an orbit just above the earth’s atmosphere with a velocity $\sqrt{1.5}$ times the velocity for a circular orbit at that height. The initial velocity imported is horizontal. What would be the maximum distance of the satellite from the surface of the earth when it is in the orbit ?
Correct answer is $2R$
Q10 Two concentric shells of masses $M_1$ and $M_2$ are situated as shown in Figure. Find the force on a particle of mass $m$ when the particle is located at (a) $r = a$ (b) $r = b$ and (c) $r = c$.
The distance $r$ is measured from the center of the shell.
Given that $OA = a, \ OB = b, \ OC = c$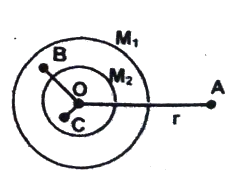
Correct answers are
(a) $\cfrac{Gm}{a^2}[M_1 + M_2]$
(b) $\cfrac{GM_2m}{b^2}$
(c) zero
Q11 Can an artificial satellite be put into orbit in such a way that it will always remain directly over New Delhi ?
Correct answer is No
Q12 How much quicker than at present must the earth revolve on its axis to make bodies at the equator experience weightlessness ? What will be the duration of day then ?
Correct answer is $17$ times, $1412$ hrs
Q13 How will weight of a body change at a height equal to earth’s radius ?
Correct answer is one-fourth
Q14 The gravitational field in a region is given by $E = (2 \hat{i} + 3 \hat{j}) \ N/kg$. Show that no work is done by the gravitational field when a particle is moved on the line $3y + 2x = 5$.
Q15 A body is weighed by a spring balance to be $1.000 \ kg$ at the north pole. How much will it weigh at the equator ? Account for the earth’s rotation only.
Correct answer is $0.997 \ kg$
Q16 Does the escape speed of a body from the earth depend on: (a) the mass of the body, (b) the location from where it is projected, (c) the direction of projection, and (d) the height of the location from where the body is launched ? Explain your answer.
Correct answer is Depends on the height of the location from where the body is launched.
Q17 A comet orbits the sun in highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed. (c) angular momentum, and (d) kinetic energy when it comes very close to the sun ?
Correct answer is Only the angular momentum is constant.
Q18 The gravitational potential at an internal point inside a solid sphere is known to be $V_r = – \cfrac{GM}{2a^3}(3a^2 – r^2)$. Find the magnitude of gravitational field at that point.
Correct answer is $\cfrac{GM}{a^3}r$ toward the center of solid sphere.
Q19 The gravitational field in a region is given by $\overrightarrow{E} = (10 \ N/kg)(\overrightarrow{i} + 2\overrightarrow{j} + 3\overrightarrow{k})$. Find the work done by an external agent to slowly shift a particle of mass $3 \ kg$ from the point $O = (0, 0, 0)$ to a point $P = (3m, 4m, 5m)$.
Correct answer is $- 780 \ J$
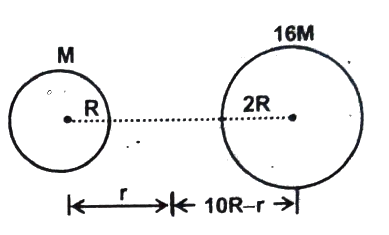
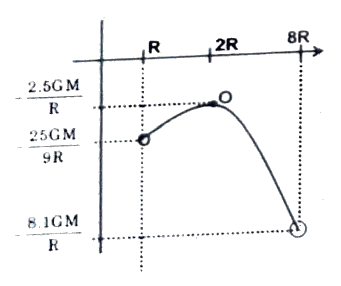
Q20 The centers of two stars of masses $M$ and $16M$ of radii $R$ and $2R$ are separated by a distance of $10R$. Draw a graph between gravitational potential $(V)$ and the distance $(r)$ from the center of the smaller star along the line joining their centers for $R \leq r \leq 8R$.
Correct answer is
Q21 Find the ratio of the kinetic energy required to be given to the satellite to escape earth’s gravitational field to the $KE$ required to be given so that the satellite moves in a circular orbit just above earth’s atmosphere.
Correct answer is $2$.
Q22 A mass equal to the mass of the earth is to be compressed in a sphere in such a way that the escape velocity from its surface is $3 \times 10^8 \ m/s$. What should be the radius of the sphere in $mm$ ? (take $GM_E = 40.5 \times 10^{13} \ Nm^2 kg^{-1}$)
Correct answer is $9$.
Q23 A body stretches a spring by a particular length at the earth’s surface at equator. At height $3\lambda \ km$ above the South Pole it will stretch the same spring by the same length. Assume the earth to be spherical. (take $\omega^2R = 0.0375$, where $\omega$ and $R$ have usual meanings). Find $\lambda$.
Correct answer is $4$.