Let’s explore circular motion! And we will begin with a brief understanding of types of circular motion (uniform and non-uniform circular motion). Following which we will quickly dive into difference between circular motion (of a particle) and rotational motion (of a rigid body, where in different particles of the rigid body may be in circular motion moving at different speeds).
Then we will get into the kinematics of the circular motion, where we will talk about the centripetal and tangential accelerations (Note: in uniform circular motion we only have centripetal acceleration), and we will also touch upon ways to determine average acceleration or average velocity over a given duration of interest.
Afterwards, we will deep dive into uniform circular motion and we will study horizontal circular motion, conical pendulum moving in a circle, circular motion of a car on a level road, circular motion of a car on a banked road and circular motion at constant speed in vertical plane.
And then we will jump into non-uniform circular motion and examine non-uniform circular motion in horizontal plane, accelerated circular motion of a car on a level road, and non-uniform motion in a vertical plane
Towards the end we will look at the simple harmonic motion of the $x$ and $y$ projections of the particle in uniform circular motion
With that, let’s start with types of circular motion for which you might want to carefully examine the video and carefully look at the involved forces and accelerations
Types of Circular Motion
In uniform circular motion, the ‘speed’ of the particle is constant. In other words, while the direction of the velocity is changing, it’s magnitude is constant. And this means that its angular velocity (number of radians covered per second) is also constant.
So what does this mean for its acceleration?
Well as we will see later when discussing kinematics of circular motion, there is NO acceleration in the direction of the velocity but there is an acceleration perpendicular to it, which is, as we will shall see later, always pointed towards the center of the circle and hence the name centripetal acceleration
In non-uniform acceleration, the magnitude and direction of the velocity of the particle are changing with time, which means it has a component in the direction of the velocity (tangential acceleration) and an acceleration perpendicular to it’s direction (centripetal acceleration) which rotates the velocity vector.
Now before we get into the kinematics of circular motion, let’s understand the difference between two similar terms circular motion and rotational motion
Difference between Circular and Rotational Motion
Circular motion typically refers to the motion of particle along a circle while rotational motion refers to rotation of a rigid body about some axis. Note that the speed of different particles of the rigid body is different.
Now let’s explore the kinematics of circular motion.
Kinematics of circular motion
Centripetal acceleration in uniform circular motion
Let’s begin with particle in uniform circular motion and let’s determine the acceleration of this particle which is moving at constant speed.
Note that we can do so either geometrically as highlighted in the video below (Note that the direction of the acceleration is towards the center) or we can determine acceleration algebraically by writing the position vector of particle in circular motion and then using $\cfrac{d^2 \overrightarrow{r}}{dt^2}$ to determine the acceleration vector $\overrightarrow{a}$
Now let’s derive the expression for centripetal acceleration algebraically
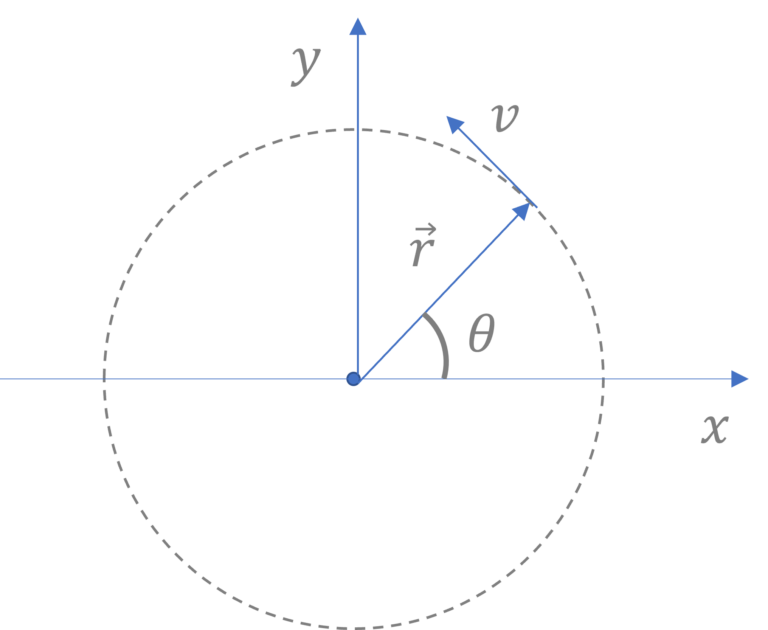
When the position vector of the particle is making an angle $\theta$ (at some time $t$), it’s position vector $\overrightarrow{r}$ can be written as:
$\overrightarrow{r} = r(\cos \theta \hat{i} + \sin \theta \hat{j})$
or $\overrightarrow{r} = r(\cos \omega t \hat{i} + \sin \omega t \hat{j})$, where angular velocity $\omega =\cfrac{v}{r}$
So, it’s acceleration at that position and time would be $\cfrac{d^2 \overrightarrow{r}}{dt^2}$
And $\cfrac{d^2 \overrightarrow{r}}{dt^2}=-\omega^2 r (\cos \theta \hat{i} + \sin \theta \hat{j})$, which we can write as
$\overrightarrow{a} =- \cfrac{v^2}{r} (\cos \theta \hat{i} + \sin \theta \hat{j})$
Note that the magnitude of $\overrightarrow{a}$ is $\cfrac{v^2}{r}$ and it’s direction is $- \hat{r}$ i.e. pointed towards the center and hence the name centripetal acceleration
Now let’s examine the accelerations in a non-uniform circular motion.
Accelerations (tangential and centripetal) in non-uniform circular motion
Here in this animation a particle is undergoing circular motion in vertical plane with string tension $T$ and gravitational force $mg$ acting on it. Note that since there are no dissipative forces, total mechanical energy of the particle remains constant i.e. $U + K = $ constant at all times. And as you will expect, kinetic energy $K$ will be maximum at the bottom and potential energy $U$ will be maximum at the top.
Also note that gravitational force, $mg \hat{k}$, is constant at all times though tension $T$ is constantly changing in magnitude and direction. $T$ is maximum at the bottom $T = mg + m \cfrac{v^2}{r}$ and it will be minimum at the top $T = m\cfrac{v^2}{r} – mg$
So, as mentioned before, non uniform circular motion refers to scenarios where in the speed of the particle is also changing as it is moving along a circular path. In such cases, particle has tangential as well as centripetal acceleration. Note that magnitude of centripetal acceleration ($=\cfrac{v^2}{r}$) is changing as speed $v$ is changing with time.
And once again, centripetal acceleration changes the direction of velocity vector while tangential acceleration changes the magnitude of velocity vector (i.e. speed $v$)
Now let’s deep dive into commonly encountered examples of uniform and non-uniform circular motion in text and we will try and understand a bit about the forces acting on the particle in circular motion
Uniform Circular Motion Examples
Uniform Circular Motion | Horizontal Motion
Given that a mass, tied to one end of a spring of spring constant $k$, is rotating in a circle with constant speed $v$ or angular velocity $\omega=\cfrac{v}{r}$. How would you determine the radius of circle, given that the natural or free length of the spring is $l$?
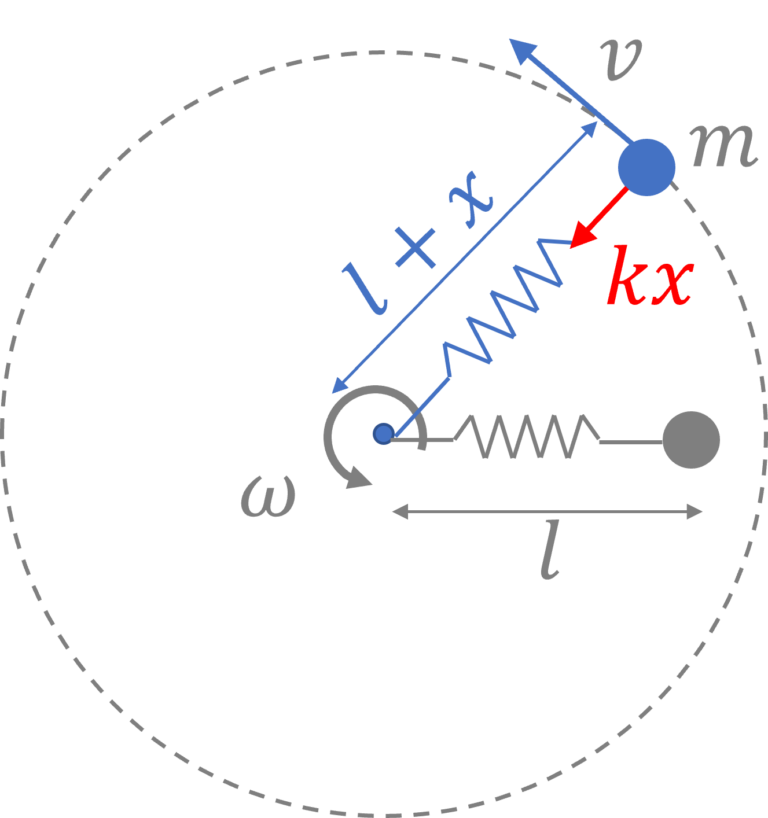
We are interested in finding $l+x$ where $x$ is the amount by which spring is stretched.
So, let’s start with writing the force acting on the mass
$F = -kx$, with minus sign indicating that the force is a restoring force and as such, it will be pointed towards the center of the circle. Going forward we will drop the minus sign.
Now, given that the particle is moving around the circle at speed $v$, it will have a centripetal acceleration $a _r= \cfrac{v^2}{l+x}$
Now, as per newton’s 2nd law, force acting on the particle $F$ and its acceleration $a_r$ must be related by the relation $F=ma_r$, So we have $kx = m \cfrac{v^2}{l+x}$, solving which we will get $x$ and thus the radius of circle traced by the particle will be $l+x$.
With that let’s explore the motion of conical pendulum moving in a circle.
Uniform Circular Motion | Conical Pendulum moving in a circle
Let’s say that the string makes an angle $\theta$ with the vertical.
So, there are two external forces acting on the mass $m$, gravitational force $mg$ pointed vertically downwards and tension $T$ acting along the string as shown.
Now, there is no acceleration in the vertical direction, so net forces in the vertical or $y$ direction must be zero i.e. $F_{net,y} = T \cos \theta – mg = 0$ or $T \cos \theta = mg$
As for the horizontal direction, at any given point in time, there is a centripetal force in the amount $T \sin \theta$ pointed towards $O$ and since the mass is moving at speed $v$, it has a centripetal acceleration in the amount $\cfrac{v^2}{r}$ (in the inertial frame of reference)
So as per newtons 2nd law $F=ma$, along the radius $T \sin \theta = m \cfrac{v^2}{r}$
Solving the two equations we can determine the desired unknown.
Note that you may choose to write the equations in a frame of rotating at the same angular speed in which the observer in that reference frame will report that the particle is stationary and there is a centrifugal force in the amount $ma$ pointed radially outwards. (If you look closely you go from $F = ma$ in the inertial frame of reference to $F-ma = 0$ in the accelerated frame of reference i.e. you treat it as a force balance problem in the accelerated frame of reference)
Uniform circular motion | circular motion of a car on a level road
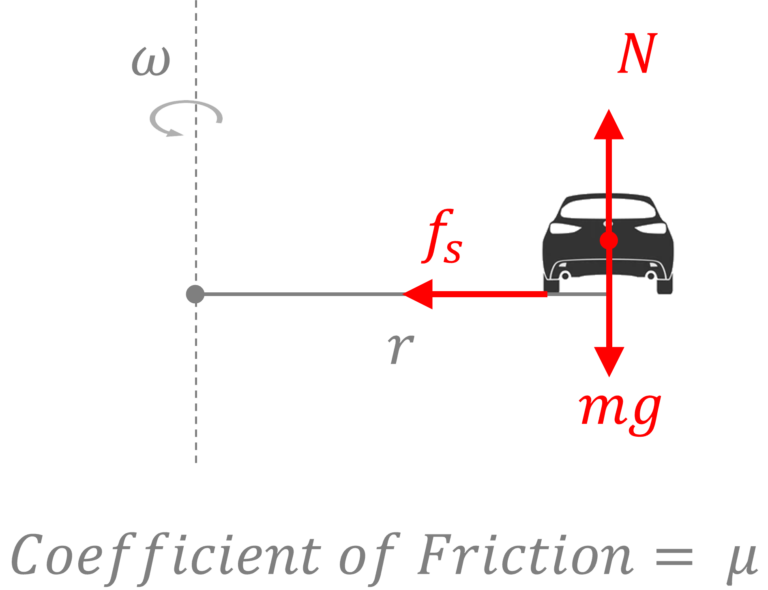
Given that the coefficient of friction $= \mu$, let’s find the limiting speed of the car (beyond which the car will slip outwards)
Now the limiting frictional force, pointed towards the center of the circle, $=\mu mg$ and centripetal acceleration $=\cfrac{v^2}{r}$ (Note $v = \omega r$
So, using the newton’s 2nd law $F = ma$, we get $f_s = m \cfrac{v^2}{r}$ and in the limiting scenario, we will have $\mu mg = m \cfrac{v^2_{max}}{r}$ or $v_{max} = \sqrt{\mu g r}$
Now, let’s see how the scenario changes a bit when the car is on a banked road
Uniform Circular Motion | Car on a banked road
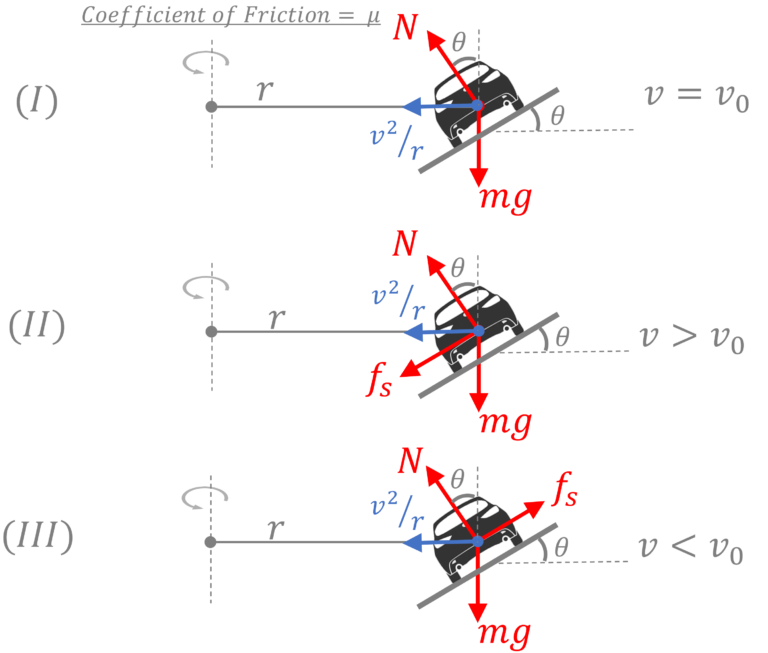
There are 3 possible scenarios depending on the speed of the car, $v$.
I) For certain speed $v_o$, there is no friction force between the car and the ground
II) For $v>v_o$, frictional force would act down the incline as shown
III) For $v<v_o$, frictional force would act up the incline as shown
So, let’s begin with establishing $v_o$ for which frictional force, $f_s = 0$
In this scenario, $N \cos \theta = mg$ and $N \sin \theta = m \cfrac{v_o^2}{r}$. Dividing the two equations we get $v_o = \sqrt{gr \tan \theta}$.
For $v> v_o$, $N \sin \theta$ will not be able to provide the needed centripetal force and the car would have tendency to slip outwards (up the incline) and as such a frictional force would kick in. Now, the two equations in the vertical and horizontal direction would become
$N \cos \theta = mg + f_s \sin \theta$ and
$N \sin \theta + f_s \cos \theta = m \cfrac{v^2}{r}$
Solving the two we can find the desired unknown. Note, to find $v_max$ at which car is about to slip, use $f_s = \mu N$
We trust that you will be able to write equations for the 3rd scenario on your own.
With that, now let’s explore the motion of a daredevil’s bike tracing a vertical circular path at a constant speed
Uniform Circular Motion | Vertical Circular Motion
Here let’s determine the normal force and frictional force on the bike at different points along the circular path
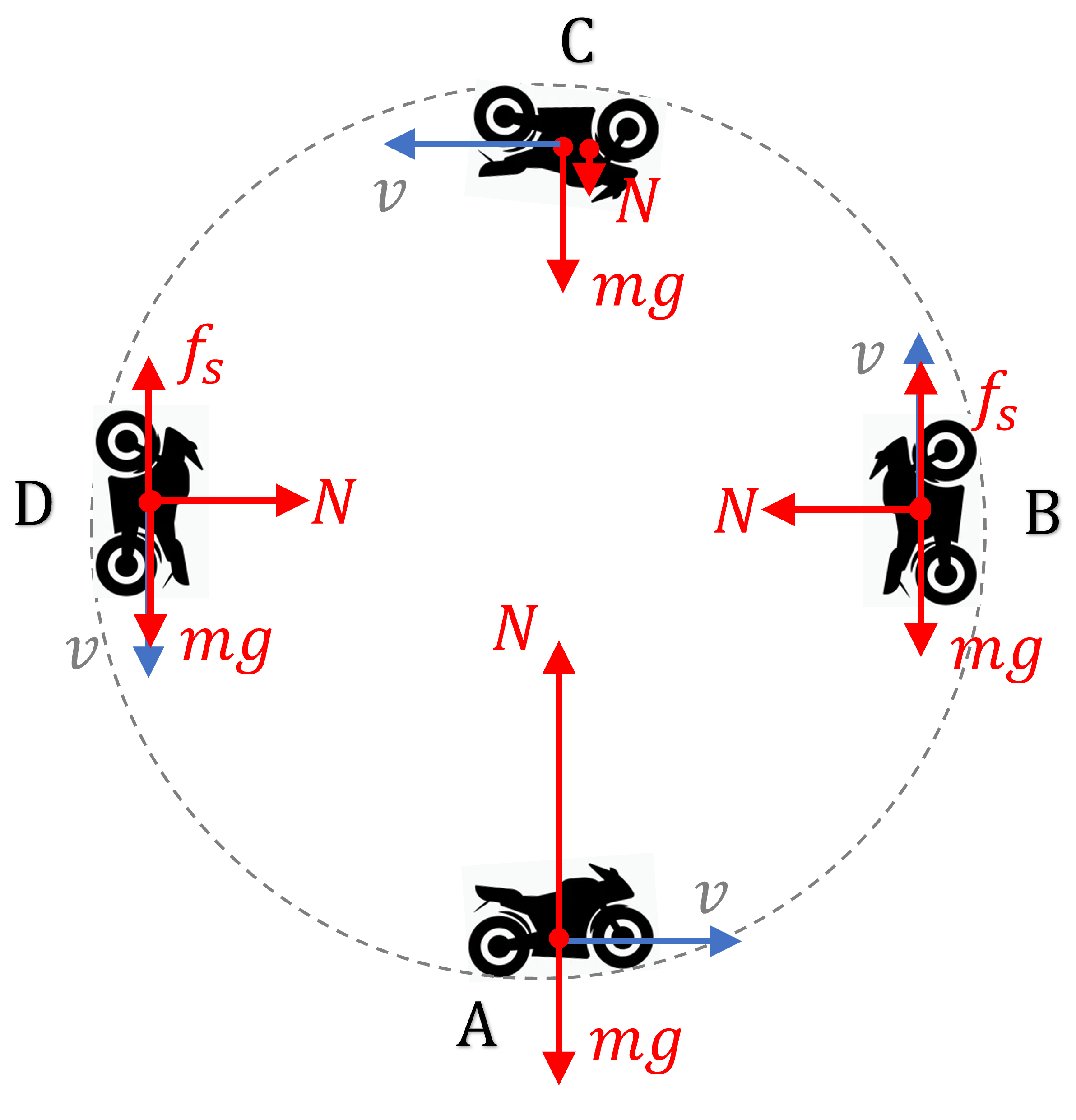
At A: $N = mg + \cfrac{mv^2}{r}$ and $f_s = 0$
At B: $N = \cfrac{mv^2}{r}$ and $f_s = mg$
At C: $N = \cfrac{mv^2}{r} – mg$ and $f_s = 0$
At A: $N = \cfrac{mv^2}{r}$ and $f_s = mg$
With that, we will now move to non uniform circular motion
Non uniform circular motion
In non-uniform circular motion, particle has a centripetal component as well as tangential component of the acceleration. The tangential component results in a change in its speed while the centripetal component of the accelerations changes direction of the velocity vector.
So let’s go ahead and look at some examples of non uniform circular motion in horizontal and vertical planes.
Non Uniform Circular Motion Examples
Non uniform circular motion | Accelerated circular motion of a car on a level road
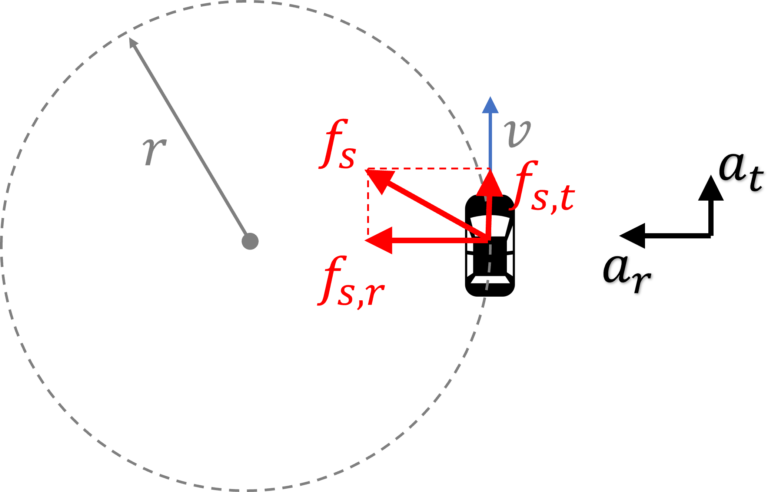
Here a component of the frictional force, $f_{s,t}$, is providing the tangential acceleration $a_t$ and another component $f_{s,r}$ is providing the centripetal acceleration
So, $f_{s,t} = ma_t$ and
$f_{s,r} = \cfrac{mv^2}{r}$
In the about to slip situation (i.e. when $f_s = \mu mg$), we will have
$\sqrt{f_{s,t}^2 + f_{s,r}^2} = \mu mg$
Non Uniform Circular Motion | Vertical Circular Motion
Here is the particle is moving under the influence of gravitational force $mg$ and tension $T$. And since there are no dissipative forces involved here, the total mechanical energy ($=U+K$) will remain constant.
So, what is the minimum speed that the particle should have at the bottom, i.e. $v_b$ such that it completes the circle.
Well, to complete the circle, at the very top $\cfrac{mv_t^2}{r} \geq mg$ in other words speed at the top should be sufficient enough so that all of $mg$ is consumed in turning the direction of velocity at that point. Note that when $mg = \cfrac{mv_t^2}{r}$, tension $T$ is zero at the very top.
or $v_{t,min} = \sqrt{gr}$.
So, how much should $v_{b,min}$ be in order to have $v_{t,min} = \sqrt{gr}$.
Well using conservation of mechanical energy, $U_b + K_b = U_t + K_t$, where assuming $U_b = 0$, $U_t$ would be $2mgr$, we will get $v_b = \sqrt{5gr}$.
Hope that helped.
Now let’s take a quick look at the motion of $x$ and $y$ projections of a particle in uniform circular motion
Simple Harmonic Motion and Uniform Circular Motion
As discussed earlier in the section on kinematics of circular motion, acceleration vector of the particle at time $t$, is given by
$\overrightarrow{a} = -\cfrac{v^2}{r} (\cos \omega t \hat{i} + \sin \omega t \hat{j})$
or $a_x = -\cfrac{v^2}{r} \cos \omega t$ and $a_y = -\cfrac{v^2}{r} \sin \omega t$.
In other words the $x$ projection is moving with an acceleration $a_x = -\cfrac{v^2}{r} \cos \omega t$ (simple harmonic motion) and $y$ projection is moving with an acceleration $a_y = -\cfrac{v^2}{r} \sin \omega t$ (also a simple harmonic motion).
And that concludes the discussion on circular motion. Hope it helped. Do drop a comment if you have any questions on this topic or have any suggestions for us.