Instructions
- Attempt all 13 multiple choice questions in section A (3 marks each) and attempt 3 out of 5 subjective questions in section B (4 marks each)
- You are allotted 1 hour
- Submit your answer sheet at the end of the exam
- Maximum Marks : 51
Section A
Q1. A body is acted upon by a force which is inversely proportional to the distance covered. The work done will be propotional to
A) $s$
B) $s^2$
C) $\sqrt{s}$
D) $k$ $ln(s/s_1)$
Correct Answer is D)
Q2. A particle of mass $m$ slides on a frictionless surface $ABCD$, starting from rest as shown in the figure. The part $BCD$ is a circular arc. If it loses contact at point $P$, find the maximum height attained by the particle from point $C$.
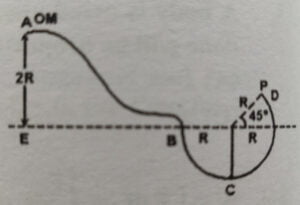
A) $R (2 + \cfrac{1}{2 \sqrt{2}})$
B) $R (2 – \cfrac{1}{2 \sqrt{2}})$
C) $3R$
D) none of these.
Correct Answer is A)
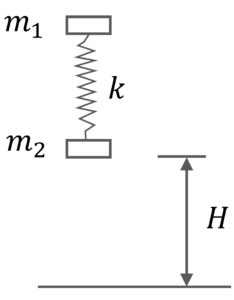
Q3. A force shown in the $F-x$ graph is applied to a $2$ Kg block horizontal as shown in the figure. The change in kinetic energy is
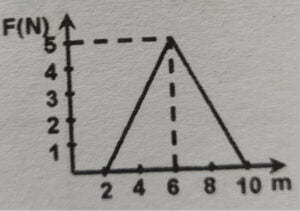
A) $15 \ J$
B) $20 \ J$
C) $25 \ J$
D) $30 \ J$
Correct Answer is B)
Q4. Two bodies $A$ and $B$, each of mass $100$ gm are allowed to move along a frictionless typical path as shown below. In order to have the same kinetic energy for both the bodies at $M$, the initial velocity that should be given to $B$, if $A$ starts from rest is
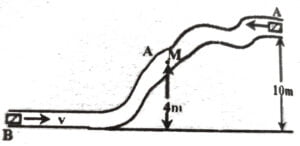
A) $10 \ m/s$
A) $\sqrt{2} \ m/s$
A) $11 \ m/s$
A) $10 \sqrt{2} \ m/s$
Correct Answer is D)
Q5. A machine delivers power to a body which is proportional to the instantaneous velocity $v$ of the body. If the body starts with a velocity that is almost negligible, the distance covered by the body is proportional to
A) $\sqrt{v}$
B) $(\cfrac{v}{2})^{1/3}$
C) $v^{5/3}$
D) $v^2$
Correct Answer is D)
Q6. A force given by the relation $F = 8t$, acts on a body of mass $2$ kg, initially at rest. Find the work done by this force on the body during first 2 seconds of its motion
A) $64$ J
B) zero
C) $-64$ J
D) none of these
Correct Answer is A)
Q7. The kinetic energy acquired by a mass $m$ in travelling a certain distance $d$, starting from rest, under the action of a force $F$ such that the force $F$ is proportional to $t$ is
A) directly proportional to $t^2$
B) independent of $t$
C) directly proportional to $t^4$
D) directly proportional to $t$
Correct Answer is C)
Q8. A projectile is fired with some velocity making certain angle with the horizontal. Which of the following graphs is the best representation for the kinetic energy of a projectile ($K.E$) versus its horizontal displacement ($x$)?
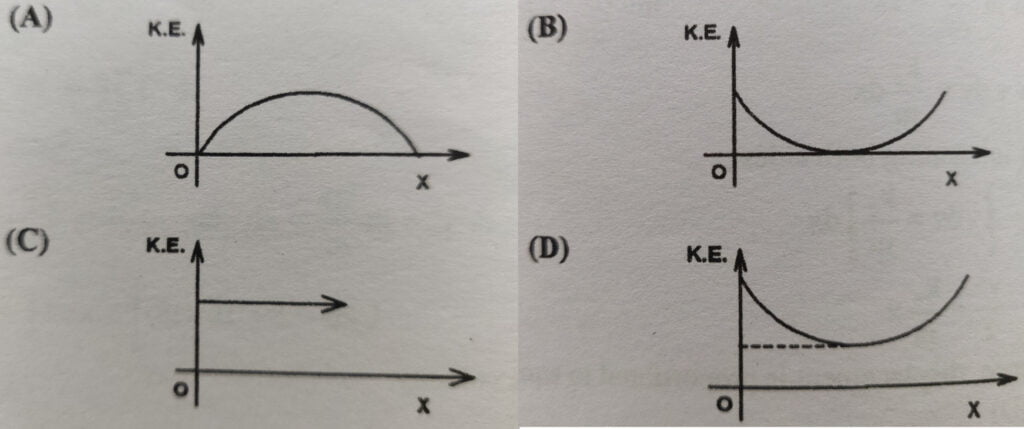
Correct Answer is D)
Q9. A particle is moving on a circle of radius $R$ such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be $v_0$ at $t=0$, the time for the completion of the half of the first revolution will be
A) $R/v_0$
B) $(R/v_0) (1-e^{-\pi})$
C) $(R/v_0) (1-e^{-2 \pi})$
D) $(R/v_0) e^{-\pi}$
Correct Answer is B)
Q10. A particle of mass $m$ is moving horizontally with a constant velocity $v$ towards a rigid wall that is moving in opposite direction with a constant speed $u$. Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
A) $(1/2) m (u+v)^2$
B) $(1/2) m (u+v)$
C) $(1/2) muv$
D) $2mu (u+v)$
Correct Answer is D)
Paragraph for Question Nos. 11 to 13
The potential energy function for the force between two in a diatomic molecule can approximately be expressed as $U(x) = \cfrac{a}{x^{12}} – \cfrac{b}{x^6}$, where $a$ and $b$ are positive constants, and $x$ is the distance between the atoms. Answer the following questions by selecting most appropriate alternative.
Q11. The graph between potential energy $U(x)$ vs $x$ will be
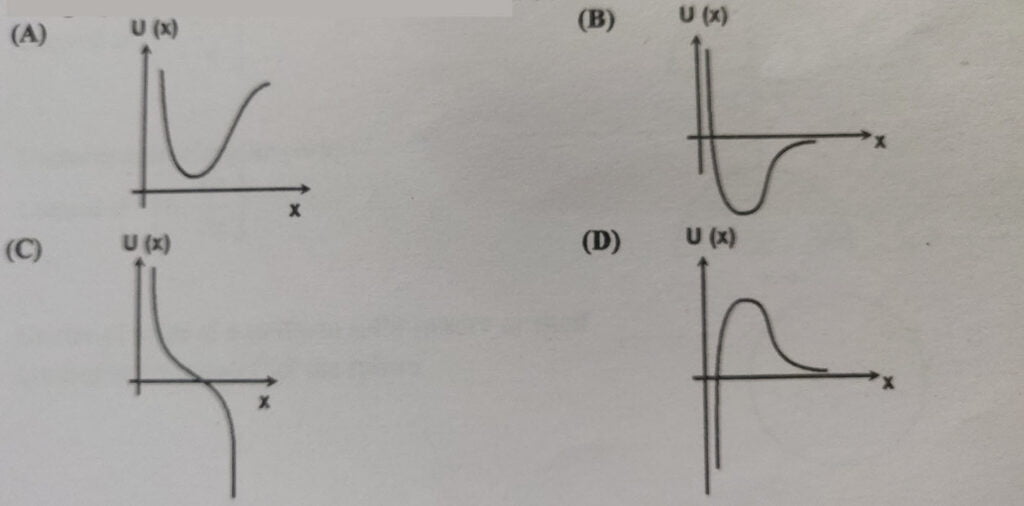
Correct Answer is B)
Q12. The dissociation energy of the molecule is (initially molecule is at rest at equilibrium)
A) $- \cfrac{b^2}{4a}$
B) $- \cfrac{b^2}{2a}$
C) $+ \cfrac{b^2}{4a}$
D) $+ \cfrac{b^2}{2a}$
Correct Answer is C)
Q13. The graph between force between the atoms $F(x)$ vs $x$ will be
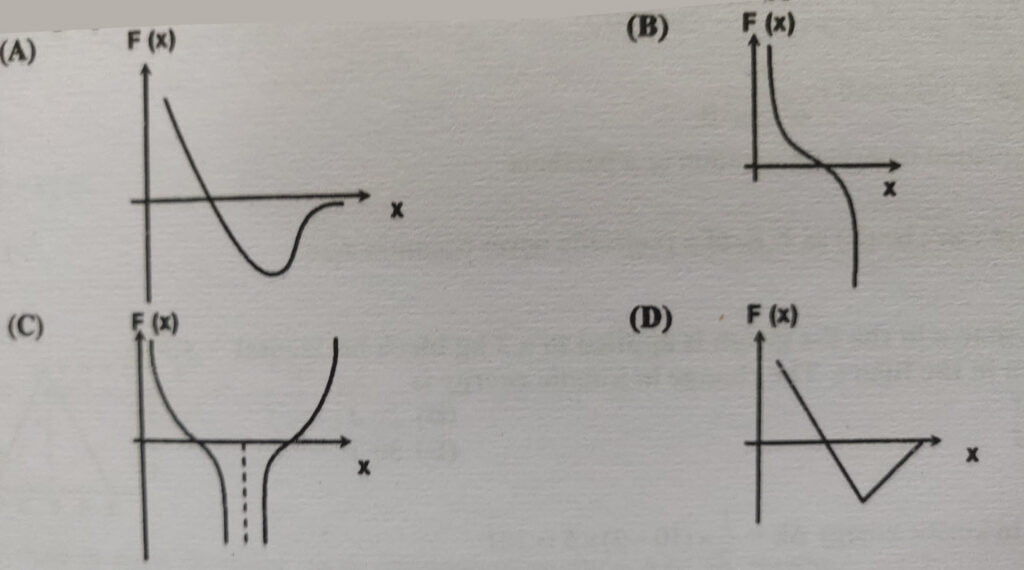
Correct Answer is A)
Section B
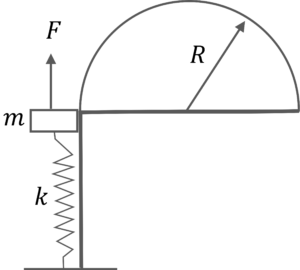
Q14. In the figure shown, a semi-cylinder of radius $R$ is rigidly fixed on a horizontal table of height $l_0$ from the ground such that there is a common edge of the table and the semi-cylinder. A block of mass $m$ is attached rigidly to a light spring of stiffness $k$, whose other end is rigidly attached to the ground. The natural length of the spring is $l_0$. A force of constant magnitude $F$ is applied on the block to move it on the frictionless surface of the semi-cylinder in a vertical plane such that the path followed by the block is a semi-circle of radius $R$
The force is always tangential to the cylinder. Find the contact force between the cylinder and the block as a function of $\theta$. The initial speed of the block is zero and the initial length of the spring is $l_0$. $\theta$ is the angular displacement of the block w.r.t the center of the circular path as shown in the figure
Q15. The arrangement shown in the diagram is moving in space with an acceleration $a = 4 \hat{i} + 4 \hat{j}$ $m/s^2$. An ideal spring of natural length $l_0$ having spring constant $k = 50$ $N/m$, is connected to block $A$. Blocks $A$ and $B$ are connected by an ideal string passing through a frictionless pulley. Mass of each block $A$ and $B$ is equal to $m = 2$ kg.
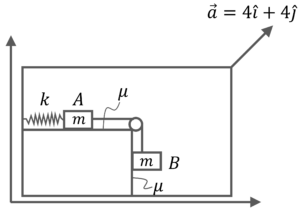
a) Calculate the minimum value of coefficient of friction so that spring remains in its natural length
b) If $\mu$ is reduced to $(9/35)^{th}$ of the original value, calculate the maximum extension of the spring.
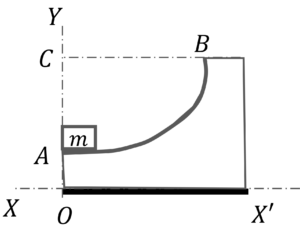
Q16. A wedge with a rough circular track $AB$, is fixed on the plane $XX$. The radius of the track is $R$ and the coefficient of friction of the track varies as $\mu = \mu_0 x$. Find the work done on mass $m$ in moving from $A$ to $B$. Here $C$ is the center of the circular track $AB$ and $x$ is the distance along +ve $x$ axis from origin $O$.
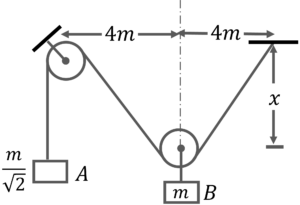
Q17. The system of mass $A$ and $B$ shown in the figure is released from rest with $x=0$, determine the velocity of mass $B$ when $x = 3$ m. Also find the maximum displacement of mass $B$.
Q18. A spring mass system is held at rest at height $H$ from the ground with the spring in the relaxed state. Find the minimum value of $H$ so that the system has a tendency to rebound after hitting the ground. The coefficient of restitution between $m_2$ and ground is zero