Here are the kinematics notes (concepts summary) which you should use for your revision. And, if you are just getting started with this chapter in class 11th, this will provide you a good overview of what to expect and which concepts to focus on.
So, let’s get started.!
The notes on kinematics concepts have been divided into four groups, as listed below. (Note that there is an audio summary of the notes for each section by Vikas Sir (IIT Delhi Alumni) which you should not miss)
1. One Dimensional Motion (concepts)
3 Two Dimensional Motion (concepts)
4 Two Dimensional Motion | Projectiles | Circular Motion | Relative Velocity (concepts)
Kinematics Notes | One Dimensional Motion (concepts)
Welcome to this podcast on, kinematics of one dimensional motion, where in we will review key concepts around motion of a particle or an object along one dimension or direction.
Here we will revisit definition of displacement, instantaneous speed & instantaneous velocity, average speed & average velocity, and instantaneous & average acceleration.
Afterwards we will briefly talk about one dimensional motion with constant acceleration, i.e. scenario in which particle is moving at constant acceleration
And we will conclude with a quick overview of scenarios where acceleration is not constant and will talk about the approach to finding the desired unknown.
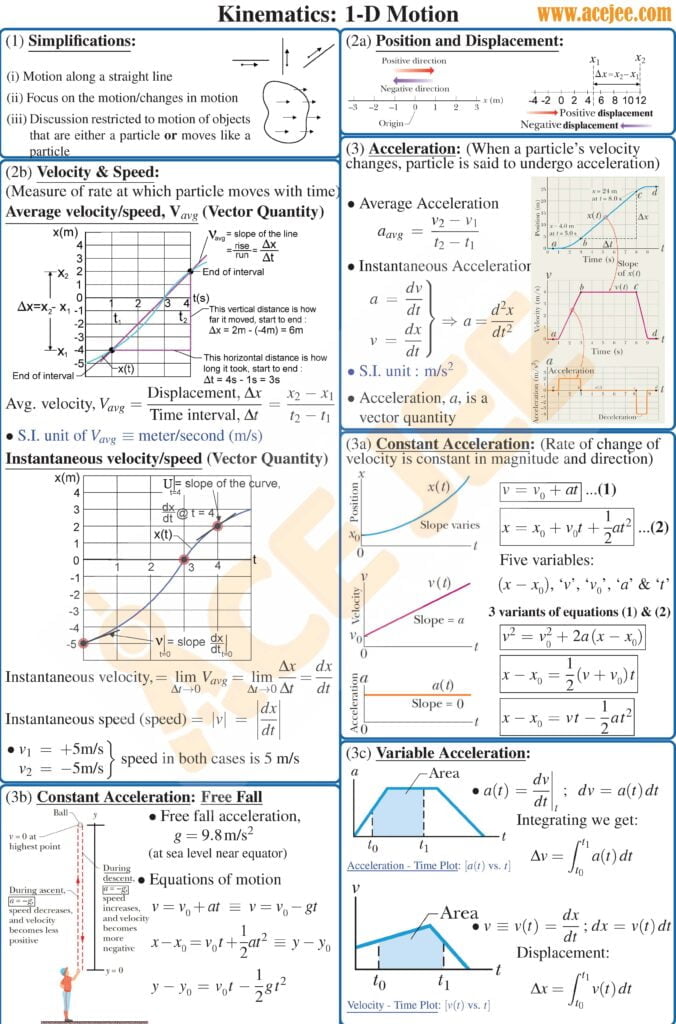
So starting with displacement, displacement is defined as final position minus initial position and is a vector quantity. So in case of one dimensional motion, displacement may be positive or may be negative depending on where the final position is with respect to initial position and note that the displacement is independent of the choice of the origin. If you didn’t understand the last statement, think about it, I am sure you will get it.
Now before we move ahead, note that distance travelled by the particle in going from initial position to final position may or may not be same as displacement. Note that the two will not be same if the particle reversed direction at some point in time in going from initial position to final position
Moving on to average speed and average velocity. Average speed, a scalar quantity, is defined as the distance travelled divided by the time taken in going from initial to final position. Average velocity, a vector quantity with magnitude and direction, on the other hand is defined as the displacement i.e. final position minus the initial position divided by the time duration. And for the reasons mentioned earlier, the magnitude of the two may or may not be same depending on whether or not distance travelled is same as displacement. In other words, average speed will be same as average velocity, in magnitude, if the particle does not reverse it’s direction. So, can you tell what the average velocity of a tennis ball thrown vertically upwards with speed v would be, between launch and the landing i.e. when it returns back to the ground and will it be same as the average speed. If in doubt, ping us.
With that, now let’s talk about the instantaneous speed and instantaneous velocity at some time ‘t’. Well instantaneous speed, a scalar quantity, is defined as distance travelled in very small or differential time dt divided by dt, while instantaneous velocity, a vector quantity, is defined as displacement in very small or differential time dt divided by dt. And how small is ‘dt’, well, it should theoretically be small enough that speed or velocity does not change significantly during that duration. And as you might be able to guess, the differential distance covered by the particle in such a small duration will be equal, in magnitude, to differential displacement and hence instantaneous speed and instantaneous velocity are same in magnitude
And before we move to a brief discussion on acceleration, note that you should become comfortable with position versus time graph, where slope of position vs time curve, representing motion of a particle, gives us the instantaneous velocity.
Now, let’s move on to average and instantaneous acceleration.
So, average acceleration, a vector quantity, is defined as final velocity minus the initial velocity divided by the time duration. It’s that simple and straightforward. And now let’s test our understanding. So, for a particle moving around a circular path with constant speed, what will be it’s average acceleration over one revolution. Well, as you would have guessed, it will be zero.
Ok, so how do we define instantaneous acceleration at some point in time t, well it is defined as change in velocity i.e. dv, divided by the small or differential time duration dt or we can say, rate of change of velocity at that time.
Now, before we move on to kinematic equations for a particle moving with constant acceleration, it is important to point out that velocity vs time graph are quite handy in describing the motion of a particle and as such, you should become comfortable with them. Note that the slope of ‘v’ vs ‘t’ graph at some time ‘t’ gives us the instantaneous acceleration at that time and the area under the curve gives us the displacement, if you assign a negative sign to the area with negative velocity and it gives us the distance travelled if you take the sum of absolute value of the area under the curve
By the way note that in acceleration vs time t graph, the area under the curve will give us the change in velocity, recall a = dv/dt or dv = a dt, so if we were to sum or rather integrate a dt over the duration of interest we will get delta v or change in velocity.
With that, let’s talk about the kinematic equations of motion for a particle moving at constant acceleration.
I trust that you will be able to refer to any standard text to understand the derivation of these kinematic equations for motion with constant acceleration, where the equations would be derived either graphically using ‘v’ vs ‘t’ graph or algebraically by integrating dv = a dt and dx = v dt.
Here we will just talk these equations from application standpoint.
So, you will come across 5 equations for motion under constant acceleration
v = u + at
Displacement, s = x_f – x_i = ut + 1/2 at^2
v^2 = u^2 + 2as
s = vt – 1/2 at^2
s = 1/2(v+u) t
Now it is important to note that there are only 2 independent equations, that means you can derive other 3 from any two of these equations. Moreover you can only determine two unknown variables. Once again you can determine only two unknowns from these equations.
So how many variables are there. Well there are 5: initial velocity u, final velocity v, displacement s, which is simply final position minus the initial position, acceleration ‘a’ and time duration ‘t’
Note that any of these 5 equations has 4 variables in it. so depending on what you have been asked to determine, you can choose the appropriate equation. Though most commonly used equations are v = u + at, s = u t + 1/2 at^2 and v^2 = u^ + 2 as.
So what else is important as you are learning to apply these equations. Well, choose your origin and coordinate axes and stick with it. For example, for a particle thrown vertically straight up from a height, you can choose the positive y-axis to be pointed up or pointed downwards and you can choose your origin at the ground or at the launch point, it doesn’t really matter, but once you make a choice then make sure you carefully write down the signs of initial velocity u, acceleration a and carefully write the expression for displacement. Rest will be simple maths beyond that point.
Hope that helped but key would be to practice different types of questions and practice regularly. So make sure that you cover all the question types and associated practice questions on the AceJEE platform.
Best Wishes
Kinematics Notes | Vectors (concepts)

Welcome. In this podcast we will briefly talk about vectors, physical quantities with magnitude and direction, which follow the laws of vector algebra.
Note that the treatment of vectors here in this podcast is from the perspective of physics which will help us apply physics concepts to two or three dimensional situations
So, to begin with, what did we mean by laws of vector algebra. Well, by laws of vector algebra we mean laws pertaining to addition of vectors, their multiplication with a scalar and multiplication of one vector with the other.
Ok, now before we dive into the vector algebra, let’s quickly talk about the unit vector notation of a vector. So, we can express any vector in three dimensions in terms of unit vectors i, j, and k along three perpendicular cartesian coordinate axes x, y, and z. For example, say we write vector A as Ax i + Ay j + Az k, what this means is that the projection of vector A along the x-axis is Ax, it’s projection along y axis is Ay and projection along z axis is Az, and, length of vector A is equal to square root of Ax^2 + Ay^2 + Az^2 and if want to know the angle that this vector makes with say x-axis, it is cos inverse of component of vector along that axis i.e. Ax divided by length or magnitude of vector A.
Ok, and now that we have used the phrase unit vector, what is it. Well is simply a vector of magnitude 1 in the direction of interest. So what will be the unit vector along the direction of vector A. Well that will be vector A divided by its magnitude.
With that, now let’s talk about vector algebra and let’s address the statement made in the beginning that vector is a physical quantity with magnitude and direction and it follows the laws of vector algebra. So can you think of a physical quantity which has a magnitude and a direction but is NOT a vector. Well, angular displacement is one such quantity. So angular displacement has a magnitude, it has direction i.e. in 2D it can be clockwise or anticlockwise but still it is not a vector because it does not follow the commutative law of vector addition. i.e vector A + vector B is not equal to vector B + vector A in case of angular displacement. Not convinced. Well take a thick book and rotate it by 90 degrees along one of its edges and then rotate it by 90 degrees along one of the other edges. Note down the final position of the book. Now bring the book back to original position and switch the order of rotation about the two edges and you will see that the final position of the book has changed.
Ok. before we move forward and talk about two different ways in which we can multiply vectors i.e. a scalar product and a vector product, note that while angular displacement is not a vector but angular velocity and angular acceleration are.
With that, let’s quickly talk about scalar product and vector products.
Scalar product as the name suggests gives a scalar result when we multiply two vectors. And we can write the result of scalar product between two vectors say A and B in two ways. AB \cos \theta where A and B are their magnitudes and theta is the angle between the two vectors or we can express the scalar product in terms of their x, y and z components as AxBx + AyBy + AzBz. These two definitions together allow us to algebraically deduce the angle between two vectors whose unit vector notations are known. Now an interesting use case from the exam point of view is, finding angle between two vectors for which unit vector notation is not given rather some relation is given between their magnitudes. For example, given that vector P plus vector Q is equal to vector R and given that magnitude of P and resultant vector R is equal. What is the angle between vectors (2P+Q) and Q. In such cases use the relation square of magnitude of vector A is equal to scalar product of A with itself i.e. A.A
Now, let’s quickly talk about cross or vector product of two vectors, result of which is a vector. And once again we can express the result of A x B as AB sin theta n cap where n cap is the unit vector perpendicular to plane of A and B and it’s direction is given by right hand thumb rule. It can also be expressed in terms of components of vectors A and B as highlighted in the notes.
And that concludes a brief overview of vectors. Once again I would recommend that you go through the different types of questions on vectors for better understanding and exam readiness.
Bye and take care
Kinematics Notes | Two Dimensional Motion (concepts)
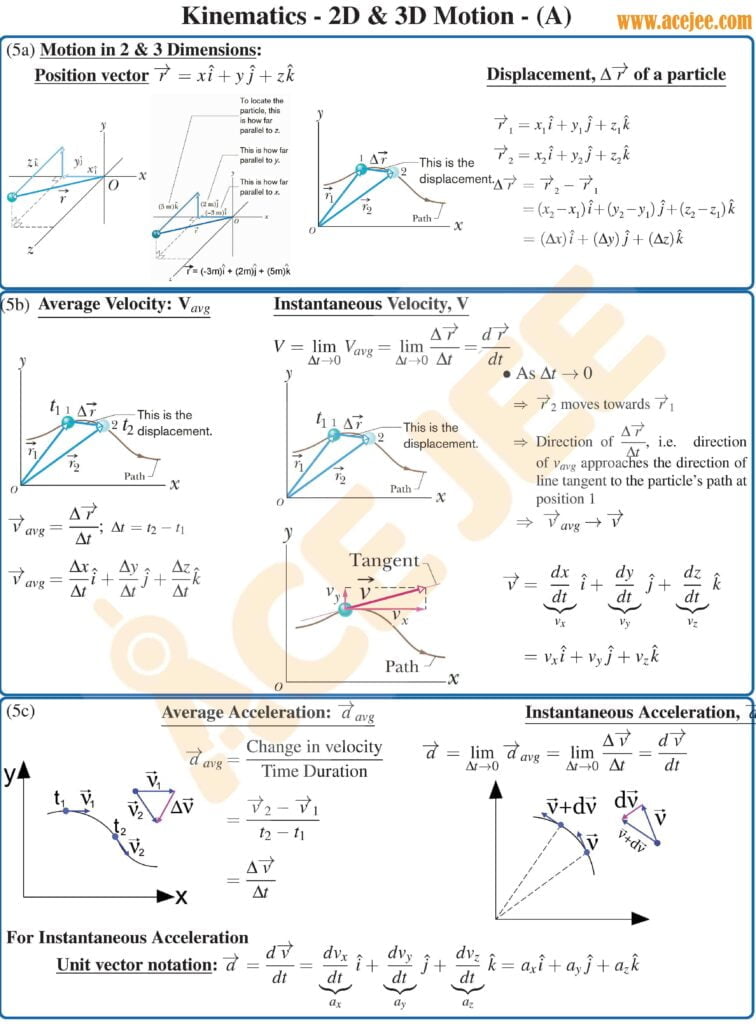
In this podcast we will expand our discussion on displacement, velocity and acceleration in one dimension to 2 dimensions. And as a heads up, you might want to refer to notes in the blog as diagrams or visual representations would help.
But before we start our discussion on displacement which is a vector quantity defined as final position minus initial position, let’s quickly talk about the position vector in 2 or 3 dimensions.
So, position vector, is a vector from origin to the position of the particle at time t and let’s say that the coordinates of that point are x, y, and z. So, the position vector in the unit vector notation will be x i + y j + z k,
Now displacement vector is simply a vector from initial position to final position. So, in terms of position vectors we can write it as r_f minus r_i where r_f is the position vector of final position and r_i is the position vector of initial position.
As for average and instantaneous velocity. Average velocity is defined as net displacement i.e. final position vector minus the initial position vector divided by the time duration
And instantaneous velocity is simply defined as dr/dt or rate of change of position vector.
Note that these might sound tricky but if you spend some time with it, it is fairly straight forward and if you are struggling with vectors, make sure that you develop sufficient comfort level with vectors especially graphical representation of sum or difference of two vectors.
Moving on, once we have the instantaneous velocity vector, rate of change of velocity i.e. dv/dt will give us the acceleration vector.
Now let’s say that you have been given a situation where in a particle is moving at a constant acceleration with constant acceleration vector given by 2i + 3 j + 1 k meaning along x-direction, acceleration is 2 m/s^2, along y it is 3 m/s^2 and along z it is 1 m/s^2, then what will be it’s position at t = 2 seconds if the particle is at rest at origin at time t = 0. Well here you will need to use the kinematic equation s = ut + 1/2 at^2 for each individual direction and determine the coordinates of the position at t = 2 seconds.
So we will conclude this discussion here and discuss projectile motion in the next podcast. And if you have any questions, feel free to ping us.
Two Dimensional Motion | Projectile Motion | Circular Motion | Relative Motion (concept notes)

Welcome to the podcast on projectile motion, and relative velocity where in we will review the basics and key concepts. To develop a deeper understanding of these topics, please refer to the blogs on projectile motion and relative motion, link for which have been provided in the description of the podcast
So, starting with the projectile motion, or rather oblique projectile motion, where in a projectile is thrown at an angle with the horizontal.
In such a scenario, particle moves along the horizontal or say x direction as well as in the vertical or y – direction. Along the horizontal direction, there is no force or no acceleration, so the projectile moves through the space with constant horizontal speed but in the vertical direction, it experiences a gravitational pull mg or we can say a gravitational acceleration ‘g’ pointed vertically downwards. In other words, we can say that it in the vertical direction it moves with a constant acceleration.
So in the horizontal direction, displacement = horizontal speed of the projectile times ‘t’ while in the vertical direction, we can use the 3 commonly used kinematics equations v_y = u_y – gt, displacement in y direction = u_y t – 1/2 gt^2 and v_y^2 = u_y^2 – 2gy
Ok, now what is some of that information examiners are typically interested in about this projectile motion. Well maximum height, range and time of flight would be basic information that you would be supposed to remember or know how to calculate. But scenarios of interest might involve, maximum range which, in case of launch and landing point being at the same height, is 45 degrees. Note that put differently for a projectile to have the desired range, required speed of projection would be minimum at 45 degrees
Now, also keep in mind that for a given initial velocity range of the projectile would be same for theta and 90 – theta.
Also note that for two points along the projectile that are at the same height ‘h’, time taken by the projectile to reach those points are given by the roots of the equation h = u sin theta t – 1/2 gt^2
Ok, at times, you might be asked to determine where the projectile will hit a given profile say for example a flight of stairs
Or you might be asked to determine the radius of curvature at some point along the trajectory, which by the way is an inverted parabola,
Or you might be asked to establish the average velocity of the projectile over a given time duration during its flight
or given the equation of trajectory y = ax – bx^2, you might be asked to determine it’s initial speed, it’s angle of projection, its maximum height, its range and it’s time of flight
or you might be given two projectiles and might be asked to determine the point of their intersection
or you might be given that a projectile is launched from a moving platform and you will be given the velocity and angle of projection with respect to the moving platform and you will need to determine the initial speed and angle of projection with respect to the ground to determine the unknown.
or you might be given that a projectile is launched from a height and you might be asked to determine the time of flight and the horizontal distance it travels before hitting the ground
or you might be given that a projectile is launched along an incline and you will be asked to determine the range, time of flight and maximum height from the incline. In this scenario, an alternate way would be to choose your x-axis to be pointed upwards along the incline and y axis to be perpendicular to the incline. In which case your acceleration along x would be – g sin theta and your acceleration along y would be – g cos theta
Now before we move on to a brief discussion on relative motion, i would highly encourage you to explore all these different question types on the acejee platform and listen through the explanation video to understand how to approach them if you have any difficulty
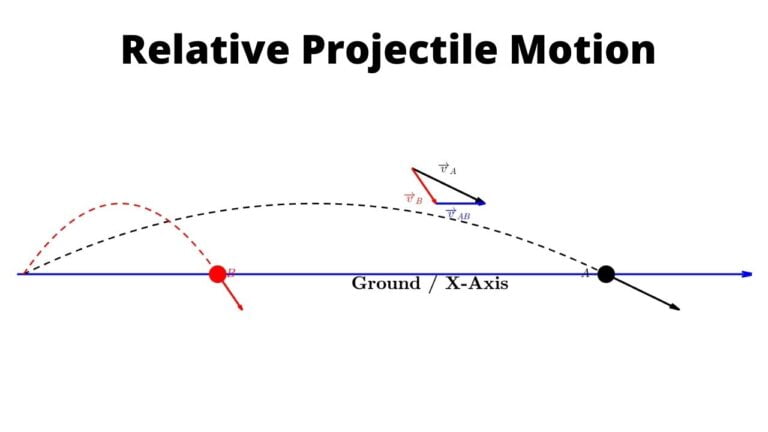
Ok, moving on to relative motion, i.e. motion of one particle as observed by another particle or observer. Here you should be able to determine relative position and relative velocity.
Relative position of say A with respect to B at some time t would simply be r_a – r_b where r_a is the position vector of A at that time t and r_b is the position vector of B at that time t. So as long as you can determine the position vectors of A and B at the time of interest, you can easily determine their relative position
As for relative velocity, I would highly recommend that you read through the blog, link for which has been provided in the description, but in summary, first of all, you need to become comfortable with determining relative velocity of one object with respect to another in one dimension i.e. in the scenario where in both the particles are moving along one dimension say along x-axis. Here if you are given their velocities with respect to ground then relative velocity of A with respect to B would simply be V_A – V_B. And if you are given the relative velocity of say a man with respect to say a train moving at some velocity then the velocity of man with respect to ground would be v_train + v_man_rel_train
Now let’s move to 2 dimensions, and to begin with let’s talk about rain man problems and problems involving say a swimmer in river
In rain man problems, you will be given that the observer is moving along the ground at some speed and rain is falling at some angle with the vertical and you might be asked to determine the velocity of rain drops with respect to man or the angle that the velocity of rain drops make with the vertical as seen by the observer. Please refer to the blog on how to approach such problems
As for the swimmer in river, you will be given the speed of swimmer relative to water and you will be given the speed of river and then you might be asked to determine the minimum time to cross the river or landing point of the swimmer or time taken by the swimmer if he has to land just opposite to his start point or you might be asked to determine the minimum velocity for him to reach the designated landing point
Moving on, in another scenario you might be given two objects moving at constant velocities in 2 dimensions and you might be asked to determine the minimum distance between the two
Or you might be given two objects that are moving under constant accelerations in 2 dimensions and you will be asked to determine the time after which they meet or collide.
And that concludes a quick overview of key concepts and problem solving skills you should develop to master this topic.
Best wishes