This blog covers section A-1 of the paper, which had 48 questions of 3 marks each. The other section (A-2) had 12 questions, 6 marks each. To access section A-2 click here
1) A sound source of fix frequency is in unison with an open end organ pipe of length $30.0 \ cm$ and a close end organ pipe of length $23.0 \ cm$ (both of same diameter). Both pipes are sounding their first overtone. If velocity of sound is $340 \ ms^{-1}$, frequency of sound source is nearly
(a) $1000 \ Hz$
(b) $1062 \ Hz$
(c) $1100 \ Hz$
(d) $1018 \ Hz$
2) Solar constant for Earth is $2.0 \ cal \ per \ cm^2$ per minute. [1 cal = 4.2 \ J]. Angular diameter of the Sun (as seen from the Earth) is $\cfrac{1}{2}^{\circ}$ ($=$ half a degree). Treating Sun as a black body, its surface temperature is estimated to be nearly
(a) $6000 \ K$
(b) $5800 \ K$
(c) $6200 \ K$
(d) $5500 \ K$
3) A concave mirror when placed in air has a focal length $f = 20 \ cm$. The mirror is now placed horizontally and filled with a thin layer of water having refractive index $\cfrac{4}{3}$. The object is placed horizontally near the principal axis at a distance $d$ from the mirror such that a real, inverted image is formed at the same plane as the object, as shown in the figure. What is the value of $d$?
(a) $30 \ cm$
(b) $20 \ cm$
(c) $15 \ cm$
(d) $40 \ cm$

4) When a sample of atoms is irradiated by neutrons, radioactive atoms are produced at a constant rate $R$, which decay with decay constant $\lambda$. The number of radioactive atoms accumulated after an irradiation time $t$ is given by
(a) $N(t) = R t e^{-\lambda t}$
(b) $N(t) = \cfrac{R}{\lambda} e^{-\lambda t}$
(c) $N(t) = \cfrac{R}{\lambda} \left( 1 – e^{-\lambda t} \right)$
(d) $N(t) = R t \left( 1 – e^{-\lambda t} \right)$
Correct answer is (c)
5) Three uncharged capacitors of capacitances $C_1 = 2 \mu F$, $C_2 = 3 \mu F$ and $C_3 = 5 \mu F$ are connected as shown in figure to one another at $O$ and to points $A$, $B$ and $D$ at potentials $V_A = 300 \ V$, $V_B = 200 \ V$ and $V_D = 400 \ V$ respectively, the potential V_o at $O$ is
(a) $300$ V
(b) $320$ V
(c) $240$ V
(d) $280$ V
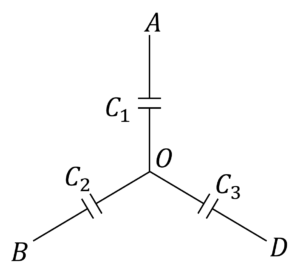
Correct answer is (b)
(a) $\cfrac{1}{2}nR(T_2 – T_1)$ $\left( \cfrac{T_2}{T_1} + \cfrac{T_3}{T_4} -2 \right)$
(b) $\cfrac{1}{2}nR(T_3 – T_2)$ $\left( \cfrac{T_3}{T_2} + \cfrac{T_4}{T_1} -2 \right)$
(c) $\cfrac{1}{2}nR(T_2 – T_1)$ $\left( \cfrac{T_3}{T_1} + \cfrac{T_3}{T_2} -2 \right)$
(d) zero
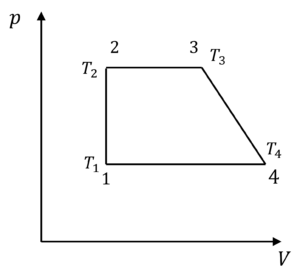
Correct answer is (b)
(a) $2A \sqrt{\cfrac{K}{M}}$
(b) $A \sqrt{\cfrac{3K}{M}}$
(c) $A \sqrt{\cfrac{K}{M}}$
(d) zero

Correct answer is (b)
8) A concave lens of focal length $10 \ cm$ is placed between two convex lenses of focal length $10 \ cm$ and $20 \ cm$ at a separation of $5 \ cm$ between the first and second lens and $10 \ cm$ between the second and third lens. An object is placed at $30 \ cm$ in front of the first convex lens. The final image is formed beyond the third lens at a distance $v$ from it. Then
(a) $v = 15 \ cm$
(b) $v = \infty$
(c) $v = 45 \ cm$
(d) $v = 20 \ cm$

Correct answer is (d)
(a) $\sqrt{1 – \cfrac{1}{\mu^2}}$
(b) $\cfrac{1}{2} \sqrt{1 – \cfrac{1}{\mu^2}}$
(c) $\cfrac{1}{2} \left\{ 1 – \sqrt{1 – \cfrac{1}{\mu^2}} \right\}$
(d) depends on $d$ and increases with increasing $d$

Correct answer is (c)
10) A convex lens is held $45 \ cm$ above the bottom of an empty tank. The image of a point object at bottom of tank is formed $36 \ cm$ above the lens. Now a liquid is poured into the tank upto a height of $40 \ cm$ above the bottom. It is found that distance of image of same point object at the bottom of the tank is $60 \ cm$ above the lens. Refractive index of liquid is
(a) $1.33$
(b) $1.37$
(c) $1.40$
(d) $1.60$
Correct answer is (d)
11) A potential of $5 \ V$ is applied across the faces of a pure germanium plate of area $2 \times 10^{4} \ m^2$ and of thickness $1.2 \times 10^{-3} \ m$. Concentraion of carriers in germanium at room temperature is $1.6 \times 10^6 m^{-3}$. Mobility of electrons and holes are $0.4 m^2 V^{-1} s^{-1}$ and $0.2 m^2 V^{-1} s^{-1}$ respectively. The current produced in germanium plate at room temperature is
(a) $1.2 \times 10^{-13}$ A
(b) $1.28 \times 10^{-9}$ A
(c) $1.536 \times 10^{-13}$ A
(d) $6.4 \times 10^{-10}$ A
Correct answer is (a)
12) Fission of one nucleus of ^{235}U releases $200 \ MeV$ energy in average. Minimum amount of $^{235}U$ required to run $1000 \ MW$ reactor per year of continuous operation (assuming $30%$ efficiency) is
(a) $1280$ ton
(b) $1.28$ ton
(c) $1.1$ ton
(d) $1.1 \times 10^3$ ton
Correct answer is (b)
13) In a young’s double slit experiment distance between slits is $d=1 \ mm$, Wavelength of light used is $600 \ nm$ and distance of screen from the plane of slits is $D = 1 \ m$. The minimum distance between two points on the screen where intensity falls to $75%$ of maximum intensity will be (Assume both souorces of equal power).
(a) $0.1$ mm
(b) $0.2$ mm
(c) $0.45$ mm
(d) $0.9$ mm
Correct answer is (a)
14) A ball is projected from horizontal ground. It attains a maximum height $H$ on its projectile path and there after strikes a stationary smooth vertical wall and falls on ground vertically below the point of maximum height. Assume the collision with wall to be perfectly elastic, the height of the point on the wall where the ball strikes is
(a) $\cfrac{3H}{4}$
(b) $\cfrac{2H}{3}$
(c) $\cfrac{H}{2}$
(d) $\cfrac{4H}{5}$
Correct answer is (a)
15) As shown in figure, a block of mass $m$ is projected from wall $A$ with velocity $2 v_o$ on the rough surface with constant sliding friction to hit the wall $B$ with velocity $v_o$. With what velocity same mass $m$ should be projected to hit the wall $B$ with same velocity $v_o$ if the surface is now moving upward with an acceleration of $a = 4g$?
(a) $2 v_0$
(b) $3 v_0$
(c) $4 v_0$
(d) $5 v_0$

Correct answer is (c)
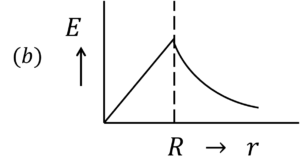
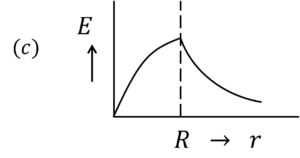
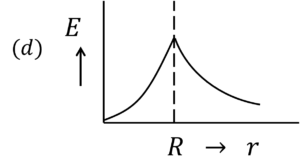
Correct answer is (d)
17) A system of capacitors $C_1 = 4 \mu F$, $C_2 = 1 \mu F$, $C_3 = 2 \mu F$ and $C_4 = 3 \mu F$ connected across a battery of emf $E=15 \ V$ is shown in figure. The charge that will flow, through the switch $K$, when it is closed, is
(a) $15 \ \mu C$ $c$ to $d$
(b) $12 \ \mu C$ $c$ to $d$
(c) $6 \ \mu C$ $d$ to $c$
(d) $9 \ \mu C$ $d$ to $c$

Correct answer is (a)
18) A simplification of a kind of interlock is shown in figure. All surfaces are smooth and frictionless. The body $m$ has a mass $m = 1 \ Kg$ and the block $M = 15 \ Kg$. The time ‘$m$’ takes to reach the base if it is released at height $h=4$ meter above the base of $M$, is [$use $g = 10 \ ms^{-2}$]
(a) $1$ s
(b) $\sqrt{3}$ s
(c) $2$ s
(d) $2 \sqrt{2}$ s

Correct answer is (d)
(a) $\cfrac{mv^2}{2(L-2nr)}$
(b) $\cfrac{mv^2}{(L-2nr)}$
(c) $\cfrac{2mv^2}{(L-2nr)}$
(d) $\cfrac{mv^2}{L}$

Correct answer is (b)
(a) $\sin^{-1} \left( \cfrac{d}{L} \right)^{\cfrac{1}{2}}$
(b) $\cos^{-1} \left( \cfrac{2d}{L} \right)^{\cfrac{1}{3}}$
(c) $\cos^{-1} \left( \cfrac{d}{L} \right)^{\cfrac{1}{3}}$
(d) $\sin^{-1} \left( \cfrac{2d}{L} \right)^{\cfrac{1}{3}}$

Correct answer is (b)
21) End $A$ of a uniform thin rod of length $2L$ is in boiling water ($100^{\circ} C$) and end $B$ is in melting ice ($0^{\circ} C$). $P$ and $Q$ are two points at distance $\cfrac{L}{2}$ from $A$ and $B$ respectively. A similar bent rod of length $\cfrac{3L}{2}$ of same material and equal cross section is joined to rod $AB$ between points $P$ and $Q$ as shown in figure. Then
(a) Temperature at $P$ will increase and that at $Q$ will decrease
(b)Rate of flow of heat will increase by $25%$
(c) Rate of flow ot heat will decrease by $20%$
(d) Rate of heat flow will increase by $37.5%$

Correct answer is (b)
22) Two stars of masses $M$ and $m$ ($M = 2m$) separated by a distance $d=3$ astronomical unit, revolve in circular orbit about their centre of mass with a period of $2$ years. If $M_s$ is the mass of Sun then
(a) $m = 2.25 \ M_s$
(b) $m = 1.25 \ M_s$
(c) $m = 2.50 \ M_s$
(d) $m = 4.50 \ M_s$
Correct answer is (a)
(a) $\cfrac{17}{2} MR^2$
(b) $44 MR^2$
(c) $22 MR^2$
(d) $\cfrac{43}{2} MR^2$

Correct answer is (c)
24) Three point charges $+q$, $-2q$ and $+q$ are placed on $x-$ axis at $x = -d$, $x=0$ and $x = +d$ respectively. The value of electric field at a point $P$ on $x-$axis at $x=r$ ($r >> d$) is given by $E = \cfrac{1}{4 \pi \epsilon_o} \cfrac{aQ}{r^n}$ (Here $Q = 2 q d^2$). Then
(a) $a = 3$, $n = 3$
(b) $a = 6$, $n = 4$
(c) $a = 3$, $n = 4$
(d) $a = \cfrac{3}{2}$, $n = 4$
Correct answer is (c)
25) The frequency of the transverse oscillations of a proton (mass $M$) trapped in a cylindrical relativistic electrom beam of circular cross section of radius $R$ and current $I$ is given by [assume that speed $v$ of relativistic electrons $\approx c$ (the speed of light in vacuum) and ignore magnetic effects]
(a) $\cfrac{1}{2 \pi R} \sqrt{\cfrac{eI}{2 \pi \epsilon_0 Mc}}$
(b) $\cfrac{1}{2 \pi R} \sqrt{\cfrac{2 \pi \epsilon_0 I}{Mc}}$
(c) $\cfrac{1}{R} \sqrt{\cfrac{2 \pi \epsilon_0 Mc}{eI}}$
(d) $\cfrac{1}{2 \pi \epsilon_0} \sqrt{\cfrac{2 \pi \epsilon_0 Mc}{eI}}$
Correct answer is
26) Current $I$ flows through a long thin walled metallic cylinder of radius $R$ with a thin longitudinal strip of width $\xi$ ($\xi << R$) running parallel to the axis of the cylinder. The magnetic induction $B$ produced at any point on the axis of the cylinder is approximately
(a) $B =$ zero
(b) $B = \cfrac{\mu_0 I}{2 \pi R^2}$
(c) $B = \cfrac{\mu_0 I \xi}{4 \pi^2 R^2}$
(d) $B = \cfrac{\mu_0 I \xi}{2 \pi R^2}$
Correct answer is (a)
27) The reading of the ammeter, used in the electrical network shown below, is $20 \ mA$, a long time after the key $K$ is closed
The reading of the ammeter, immediately after the key was closed was
(a) zero
(b) $16 \ mA$
(c) $25 \ mA$
(d) $32 \ mA$

Correct answer is (b)
28) At the Earth’s surface, a projectile is launched straight up at a speed of $10.0 \ km/s$. Height to which it will rise is [$g$ at surface of Earth $= 9.8 \ m/s^2$ and radius of earth $R = 6400 \ Km$]
(a) $1.63 \times 10^3$ $Km$
(b) $1.56 \times 10^4$ $Km$
(c) $2.52 \times 10^4$ $Km$
(d) $5.1 \times 10^3$ $Km$
Correct answer is (d)
29) A small sphere of mas $2.00 \ g$ is released from rest in a large cylindrical vessel filled with oil. The resistive force due to viscosity of oil acting on sphere is proportional to its velocity. Sphere approaches a terminal speed of $5.00 \ cm/s$. The time it takes the sphere to reach $90.0 %$ of its terminal speed is approximately.
(a) $3.22$ $ms$
(b) $5.10$ $ms$
(c) $10.2$ $ms$
(d) $11.7$ $ms$
Correct answer is (d)
(a) Zero
(b) $\cfrac{Q}{4 \epsilon_0}$
(c) $\cfrac{Q}{2 \epsilon_0}$
(d) $\cfrac{Q}{\epsilon_0}$

Correct answer is (c)
31) Three small identical neutral metal balls are at the vertices of an equilateral triangle. The balls are in turn touched to an isolated large charged conducting sphere whose centre is on a line perpendicular to the plane of triangle and passing through its center. As a result the first and second balls have acquired charges $q_1$ and $q_2$ respectively. The charge acquired by the third ball is [Assume that charge and potential of large spherical conductor change insignificantly in charging of the balls and that charges on balls are spherically symmetric]
(a) $\cfrac{q_1^2}{q_2}$
(b) $\cfrac{q_2^2}{q_1}$
(c) $2q_2 – q_1$
(d) $q_3 = q_2 = q_1$
Correct answer is (b)
32) Voltage across the load $L$ is controlled by using circuit as shown in figure. $P$ is a potentiometer. Resistance $R_L$ of the load and $R_p$ of the potentiometer are equal to $R$. Load $L$ is connected to the middle of potentiometer. Input voltage $V$ is constant. If now $R_L$ is doubled, the voltage across load will change by a factor
(a) $\cfrac{5}{4}$
(b) $\cfrac{7}{5}$
(c) $\cfrac{8}{9}$
(d) $\cfrac{10}{9}$
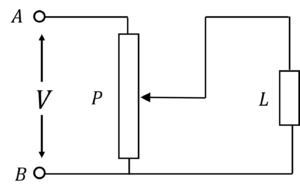
Correct answer is (d)
(a) $x = 0.173 \cos 20 t$
(b) $x = 0.1 \cos 40 \pi t$
(c) $x = -0.173 \sin \cfrac{\pi}{10} t$
(d) $x = -0.1 \sin 20 t$
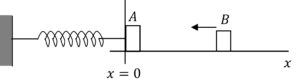
Correct answer is (d)
34) Two plane glass testing slides of surface area $A$ are stuck with each other by a small water drop squeezed between them as an extremely thin film of thickness $d$. If the surface tension of water be $T$ and the angle of contact be zero, then the force required to pull apart the two glass plates will be
(a) $8 \cfrac{TA}{d}$
(b) $4 \cfrac{TA}{d}$
(c) $2 \cfrac{TA}{d}$
(d) $\cfrac{TA}{d}$
Correct answer is (c)
35) The rate of flow of a certain liquid of viscosity $\eta$ through a horizontal capillary of length $l$ and radius $r$ is $Q$, when the pressure head at the inlet is just twice the atmospheric pressure. The rate of flow of the same liquid through another capillary of length $2l$ and radius $2r$ when the inlet pressure head is $4$ times the atmospheric pressure will be (The outlet being open to atmosphere in each case)
(a) $24 Q$
(b) $16 Q$
(c) $8 Q$
(d) $4 Q$
Correct answer is (b)
36) A uniform rod of the material of Young’s modulus $Y$ is pushed over a smooth horizontal surface by a constant horizontal force $F$. The area of cross-section of the rod is $A$. The compressional strain in the rod is
(a) $\cfrac{F}{AY}$
(b) $\cfrac{F}{2AY}$
(c) $\cfrac{3F}{2AY}$
(d) $\cfrac{2F}{AY}$
Correct answer is (b)
37) A total charge $Q$ is uniformly distributed over a non-conducting ring of radius $r$. There is a time varying magnetic field perpendicular to its plane and changing at the uniform rate of $\cfrac{dB}{dt}$. The magnitude of induced tangential electric field $E$ on ring is
(a) $r \cfrac{dB}{dt}$
(b) $r^2 \cfrac{dB}{dt}$
(c) $\cfrac{1}{2} r \cfrac{dB}{dt}$
(d) $\cfrac{1}{2} r^2 \cfrac{dB}{dt}$
Correct answer is (c)
38) DC $emf$ of $15 \ V$ is applied to a circuit containing $5 \ H$ inductance and $10 \ \Omega$ resistance in series at $t=0$. The ratio of the currents in the circuit at $t=0.5$ sec and at $t=1.0$ sec is
(a) $\cfrac{e^2}{e^2-1}$
(b) $\cfrac{\sqrt{e}}{\sqrt{e} -1}$
(c) $\cfrac{e}{e+1}$
(d) $\cfrac{1}{e}$
Correct answer is (c)
39) An insulating rod of length $l$ carries a charge $q$ distributed uniformly all over its length. The rod is pivoted at its midpoint and is rotated at a frequency $f$ (in Hz) about an axis perpendicular to the rod passing through the point at the pivot. The magnetic moment of the system is
(a) $\cfrac{1}{12} \pi q f t^2$
(b) $\cfrac{1}{6} \pi q f t^2$
(c) $\cfrac{1}{3} \pi q f t^2$
(d) $\pi q f t^2$
Correct answer is (a)
40) A circular loop of radius $r$ is placed inside another circular loop of radius $R$ ($R >> r$). The loops are coplanar and concentric. The mutual inductance ($M$) of the system is proportional to
(a) $\cfrac{r}{R}$
(b) $\cfrac{r^2}{R}$
(c) $\cfrac{R^2}{r}$
(d) $\cfrac{r^2}{R^2}$
Correct answer is (b)
41) The amplitude of the electric and magnetic fields associated with a beam of light of intensity $477.9 \ W/m^2$ are, respectively,
(a) $6 \times 10^2$ $V/m$ and $2 \times 10^{-6}$ $T$
(b) $3 \times 10^2$ $V/m$ and $1 \times 10^{-6}$ $T$
(c) $12 \times 10^2$ $V/m$ and $4 \times 10^{-6}$ $T$
(d) $9 \times 10^2$ $V/m$ and $3 \times 10^{-6}$ $T$
Correct answer is (a)
42) Given that the critical angle of incidence for total internal reflection within a transparent material when placed in air is $45^{\circ}$. The Brewster’s angle of incidence for light propagating from air to the transparent material will be
(a) $54.74^{\circ}$
(b) $35.26^{\circ}$
(c) $25.26^{\circ}$
(d) $44.74^{\circ}$
Correct answer is (a)
43) A particle moves along a straight line. Its displacement $S$ varies with time $t$ according to the law $S^2 = at^2 + 2bt + c$ ($a$, $b$ and $c$ are constants). The acceleration of this particle varies as
(a) $S^0$
(b) $S^{-1}$
(c) $S^{-2}$
(d) $S^{-3}$
Correct answer is (d)
44) A ball $A$ (of mass $m_1$) moving with velocity $v$ experiences an elastic collision with another stationary ball $B$ (of mass $m_2$). Each ball flies apart symmetrically relative to the initial direction of motion of ball $A$ at an angle $\theta$. Ratio of the masses of balls $\cfrac{m_1}{m_2}$ is
(a) $1 + 2 \cos \theta$
(b) $2 \cos 2 \theta$
(c) $1 + 2 \cos 2 \theta$
(d) $1 + \cos 2 \theta$
Correct answer is (c)
(a) Acceleration of center of cylinder is $\cfrac{F}{m}$
(b) Frictional force on cylinder acts forward
(c) Magnitude of frication force is $\cfrac{F}{3}$
(d) None of the above

Correct answer is (c)
46) A motor pump is used to deliver water at a certain rate $r$ from a given pipe. To obtain thrice as much water from the same pipe in the same time, the power of the motor has to be increased to
(a) $3$ times
(b) $9$ times
(c) $27$ times
(d) $81$ times
Correct answer is (c)
47) Two small solid balls of masses $m$ and $8 \ m$ made up of same material are tied at the two ends of a thin weightless thread. They are dropped from a ballon in air. The tension $T$ of thread during fall, after the motion of balls has reached steady state is
(a) $2$ mg
(b) $3.5$ mg
(c) $4.5$ mg
(d) zero
Correct answer is (a)
48) Obtain the value of $\cfrac{e^2}{2 \epsilon_o} hc$
(a) $0.0073$
(b) $0.0073$ m
(c) $0.073$ $s^{-1}$
(d) $0.0346$ $m^{-1}$
Correct answer is (a)