(Physics) Kinematics DPP | Daily Practice Problems (1/12)

In JEE Main, you can expect 1 to 2 questions from Kinematics while in JEE advanced (Paper 1 and Paper 2 put together) you can expect 0 to 1 question. And it might be helpful to point out that in JEE Main 2020 and 2021, we saw equal spread of questions between 1D (1 Dimensional) Motion and 2D (2 Dimensional) Motion (including Vectors) but in JEE Advanced the question primarily involves 2 dimensional motion as 2D questions tend to have higher complexity. But you should remember that Kinematics forms the foundation for chapters to come. So it is important that you get very comfortable with this chapter. So to help you practice, we have included more than 300 questions on Kinematics in AceJEE question bank and mock tests. Here, as a part of Physics DPP (Daily Practice Problems), we are sharing 2 Kinematics DPP (20 questions) along with a review of these questions with Vikas Sir
But to make the most of these practice problems and learn about steps that you need to solve Kinematics questions, I strongly recommend that you first go through the 40 question types on Kinematics and do listen through the videos on each of the question type where in Vikas Sir walk you through the concepts and step by step approach (along with a solved sample problem) that you can then apply to any question on Kinematics
Note that if you have any doubts / comments about any question, please comment down below and we will provide the supporting explanation / audio / video as appropriate. Remember problem solving is a skill that you can acquire through practice and a good understanding of concepts
Q1. The magnitude of component of $\overrightarrow{A}=$ $2 \hat{i} + 3 \hat{j} + 4 \hat{k}$ in direction of $\overrightarrow{B}=$ $4 \hat{i} + 5 \hat{j} + 6 \hat{k}$ is.
Answer
Correct answer is $\cfrac{47}{\sqrt{77}}$
Q2. The acceleration time graph of a particle is shown in the figure. What is the velocity of particle at $t = 8s$, if initial velocity of particle is 3 m/s?
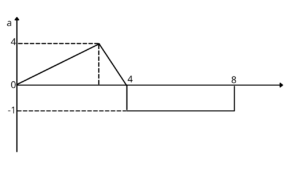
Answer
Correct answer is 7 m/s
Q3. A particle is moving along a straight line such that its position depends on time as $x = 1 – at + bt^2$, where $a = 2 m/s$, $b=1 \ m/s^2$, then distance covered by the particle during first 3 seconds from starting of the motion
Answer
Correct answer is 5m
Q4. A stone is thrown vertically upwards with an initial velocity $v_0$. The distance travelled in time $\cfrac{1.5 v_0}{g}$ is given by $\cfrac{cv_0^2}{8g}$, find the value of C.
Answer
Correct answer is 5
Q5. Considering two vectors $\overrightarrow{F}=$ $(4 \hat{i}) – 10 \hat{j}$ N and $\overrightarrow{r}=$ $(-5 \hat{i}) – 3 \hat{j}$ m, compute $\cfrac{|\overrightarrow{r} \times \overrightarrow{F}|}{31}$
Answer
Correct answer is 2
Q6. Vectors $\overrightarrow{P}$, $\overrightarrow{Q}$, and $\overrightarrow{R}$ have magnitudes 5, 12 and 13 units and $\overrightarrow{P} + \overrightarrow{Q}$ $=\overrightarrow{R}$. If angle between $\overrightarrow{Q}$ and $\overrightarrow{R}$ is $\theta$. Then find $\cfrac{13}{2} \cos \theta$
Answer
Correct answer is 6
Q7. If $\overrightarrow{A}$ and $\overrightarrow{B}$ ar two mutually perpendicular vectors, where $\overrightarrow{A}=$ $5 \hat{i} + 7 \hat{j} + 3 \hat{k}$ and $\overrightarrow{B}=$ $2 \hat{i} + 2 \hat{j} – a \hat{k}$, then find the value of $a$.
Answer
Correct answer is 8
Q8. If $\overrightarrow{A}=$ $0.4 \hat{i} + 0.3 \hat{j} + c \hat{k}$ is a unit vector. The value of $c$ is $\sqrt{K}$. Find the value of K.
Answer
Correct answer is 0.75
Q9. Find the magnitude of a given vector whose end points are (4, -4, 0) and (-2, -2, 0). (take $\sqrt{10}=3.16$)
Answer
Correct answer is 6.32
Q10. A bulb is accidentally dropped from the ceiling of a train moving with constant velocity. What shape of the path will be seen from an observer on the ground?
Answer
Correct answer is parabolic
Q11. A cabin is moved up the inclined plane with constant acceleration $g \sin \theta$. A particle is projected with some velocity with respect to the cabin in a direction perpendicular to the inclined plane. If maximum height attained by particle perpendicular to inclined plane is same as range of particle with respect to the cabin parallel to plane, then calculate values of $\cot \theta$

Answer
Correct answer is 8
Q12. Two boats A and B move away from buoy anchored at the middle of a river along mutually perpendicular straight lines, the boat A moves along the river and the boat B across the river. Having moved off an equal distance from the buoy the boat returned. Find the times of motion of boats $\cfrac{t_A}{t_B}$, if the velocity of each boat with respect to water is $n$ times greater than the stream velocity.
Answer
Correct answer is $[\cfrac{n}{\sqrt{n^2 – 1}}]$
Q13. A train of length $200\ m$ switches on its headlight when it starts moving with acceleration $0.5 \ m/s^2$. Some time later, its tail light is switched ON. An observer on the ground notices that the two events occur at the same place. The time interval between the two events is $K \times 10 \sqrt{2}$. Then find the value of $K$
Answer
Correct answer is 2
Q14. A particle starting from rest moves in a straight line with acceleration as shown in $a-t$ graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
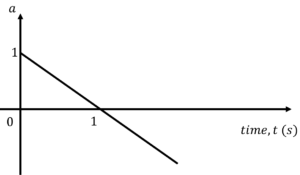
Answer
Correct answer is 4
Q15. A bead moves along straight horizontal wire of length L, starting from the left end with a velocity $v_0$. Its retardation is proportional to the distance from the right end of the wire. Find the initial retardation (in $m/s^2$) (at left end of the wire). If the bead reaches the right end of the wire with a velocity $\cfrac{v_0}{2}$. (given $v_0 = 5$ m/s and $L=1$ m)
Answer
Correct answer is 18.75
Q16. A particle is projected from the ground at an angle with the horizontal. The velocity of the projectile when it is at the greatest height is $\sqrt{\cfrac{3}{5}}$ times when it is at one third of its greatest height. The angle of projection is $2K^\circ$. Find the value of K.
Answer
Correct answer is 22.50
Q17. A stone is projected at an angle $45^\circ$ with horizontal. A bee follows the trajectory of the stone at a constant speed equal to the initial speed of the stone. Neglect air resistance for motion of stone. If the magnitude of acceleration of the bee at the topmost point of its trajectory is (4.9)k $m/s^2$. Find the value of k. (g = 9.8 $m/s^2$)
Answer
Correct answer is 4
Q18. The following figure shows the velocity and acceleration of a point like body at the initial moment of its motion. The acceleration vector of the body remains constant. The time (in sec) after which its speed becomes 8 m/s again is
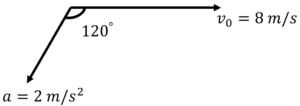
Answer
Correct answer is 4
Q19. At what speed (in m/s) must a pebble be thrown from a height of h = 3.6 m, and at an angle of $30^\circ$ measured from the horizontal, if it is to hit the ground at an angle of $45^\circ$. (Air drag can be neglected.) (Take g = 10 $m/s^2$)
Answer
Correct answer is 12.00
Q20. A motor car moving with a uniform speed of 20 m/s comes to stop on the application of brakes after traveling a distance of 10 m. Its magnitude of acceleration is
Answer
Correct answer is 20
Solution of Q1 to Q5 - with Vikas Sir
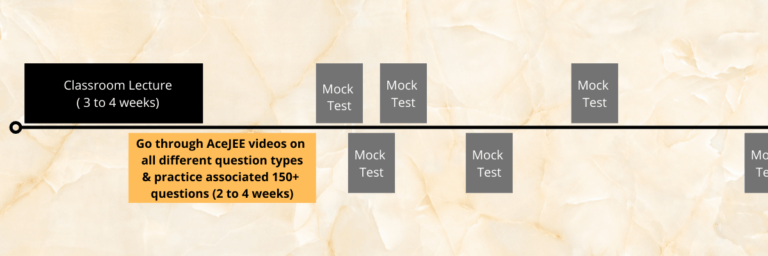
Additional Practice Problems
Recommended Study Plan