Moment of inertia or mass moment of inertia is the resistance of a rigid body to change in its angular velocity or we can say, resistance to angular acceleration, when a net external torque acts on it (similar to resistance offered by mass of a particle to acceleration, when a net force acts on it). In this blog we will explore moment of inertia formula for different shapes (ring, disc, hollow cylinder / annular disc, ring/disc (about an inclined axis), solid cylinder, rod, rod (about an inclined axis), sphere, hollow sphere, rectangle / rectangular plate, square plate, cube, triangle, cone
For a rigid body made up of discrete particles (for example a pendulum with bob of mass $m$ and massless rod of length $l$), moment of inertia can be calculated using the formula $I = \sum_i m_i r_i^2$
For a continuous rigid body (for example a uniform solid sphere or a uniform rod etc.), $I = \int r^2 dm$
Unit of moment of inertia $I$ is $Kg \ m^2$
Dimensional Formula = $[M^1L^2T^0]$
Now, let’s look at the moment of inertia for different shapes, but before we do that, let’s review the parallel axis and perpendicular axis theorem
Parallel Axis Theorem
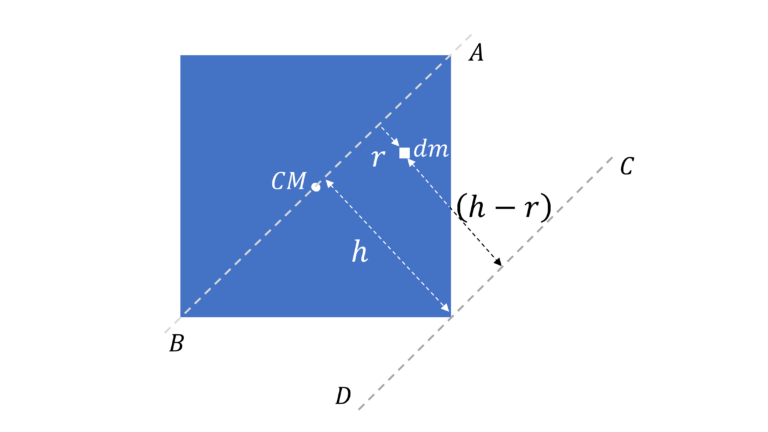
$I = I_{CM} + Mh^2$
Derivation
Moment of Inertia about $AB$, $I_{CM}$ $=\int r^2dm$
Moment of inertia about $CD$ (parallel to $AB$), $I =\int (h-r)^2 dm$ $=\int (h^2 + r^2 -2hr)dm$ $= \int r^2dm +$ $h^2 \int dm -$ $2h \int rdm$
Now, $\int r dm = M r_{CM} = 0$ as the axis $AB$ is passing through the center of mass (ping us if this didn’t make sense)
Or, $I = I_{CM} + Mh^2$
Perpendicular Axis Theorem (valid ONLY for planar objects)
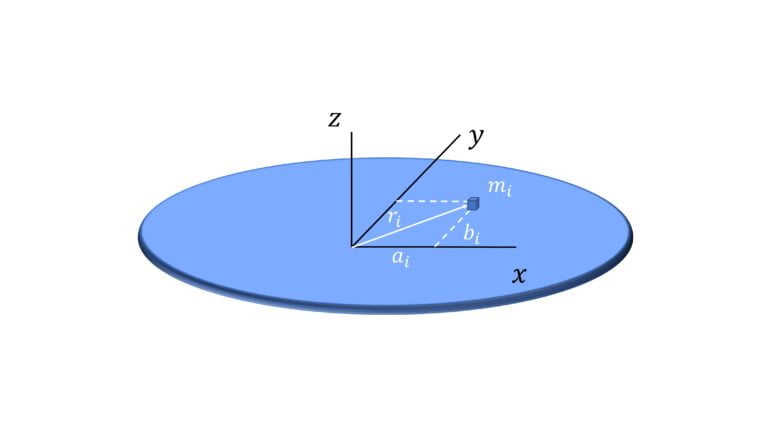
$I_z = I_x + I_y$
Derivation
$I_z = \sum_i m_i r_i^2$ $= \sum_i m_i (a_i^2 + b_i^2)$ $=\sum_i m_i a_i^2 + $ $\sum_i m_i + b_i^2$ $=I_x + I_y$
Non – Planar Objects:
Note perpendicular axis theorem is NOT valid for non planar or 3 dimensional objects like a cube.
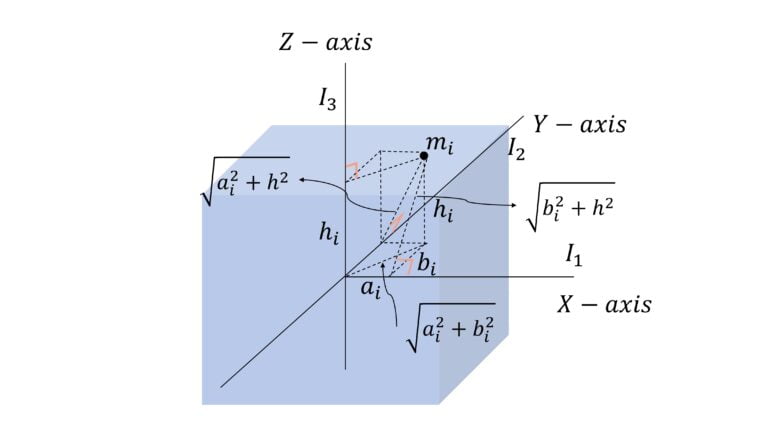
$I_z \neq I_x + I_y$
Reason
$I_z = \sum_i m_i (a_i^2 + b_i^2$
$I_x = \sum_i m_i (b_i^2 + h_i^2)$
$I_y = \sum_i m_i (b_i^2 + h_i^2)$
Moment of Inertia of Ring
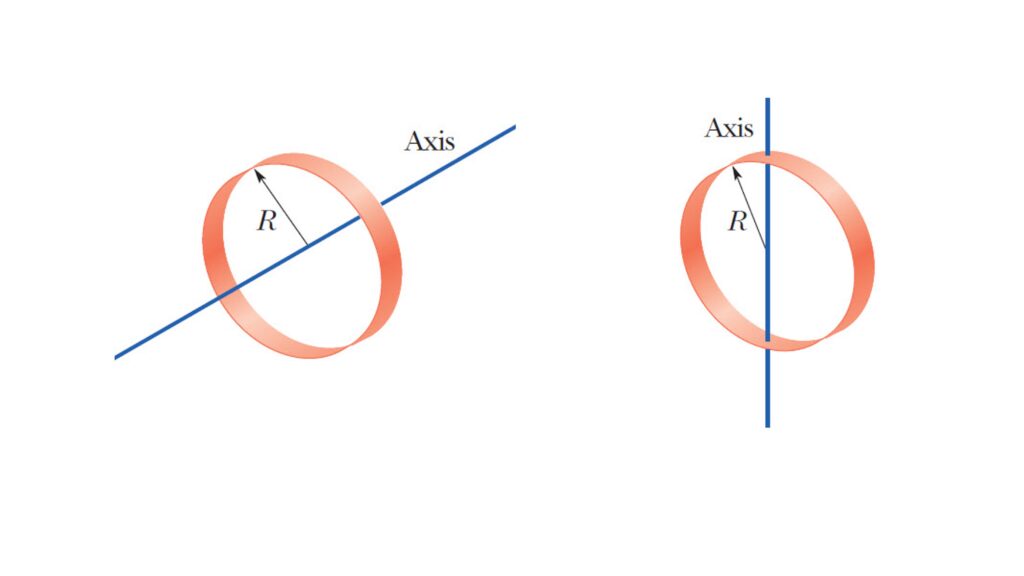
About the central axis (passing through its center and perpendicular to the plane of the ring):
$I = MR^2$
About the diameter:
$I = \cfrac{1}{2} MR^2$
About the central axis (passing through the center of the ring and perpendicular to the plane of the ring):
$I = \int R^2 dm$ $= R^2 \int dm$ $= MR^2$
About its diameter:
Using perpendicular axis theorem $I_z = I_x + I_y$, we will get $I = \cfrac{1}{2} MR^2$
Moment of Inertia of Disc
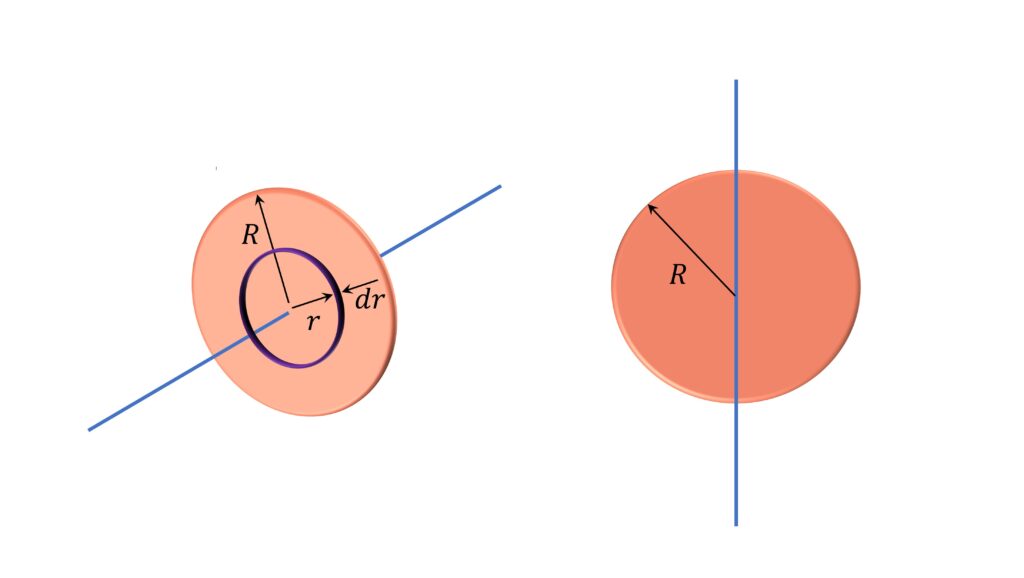
About the central axis (axis passing through the center and perpendicular to the plane of the disc)
$I = \cfrac{1}{2}MR^2$
About its diameter:
$I = \cfrac{1}{4}MR^2$
Moment of Inertia of Ring / Disc About an Inclined Axis
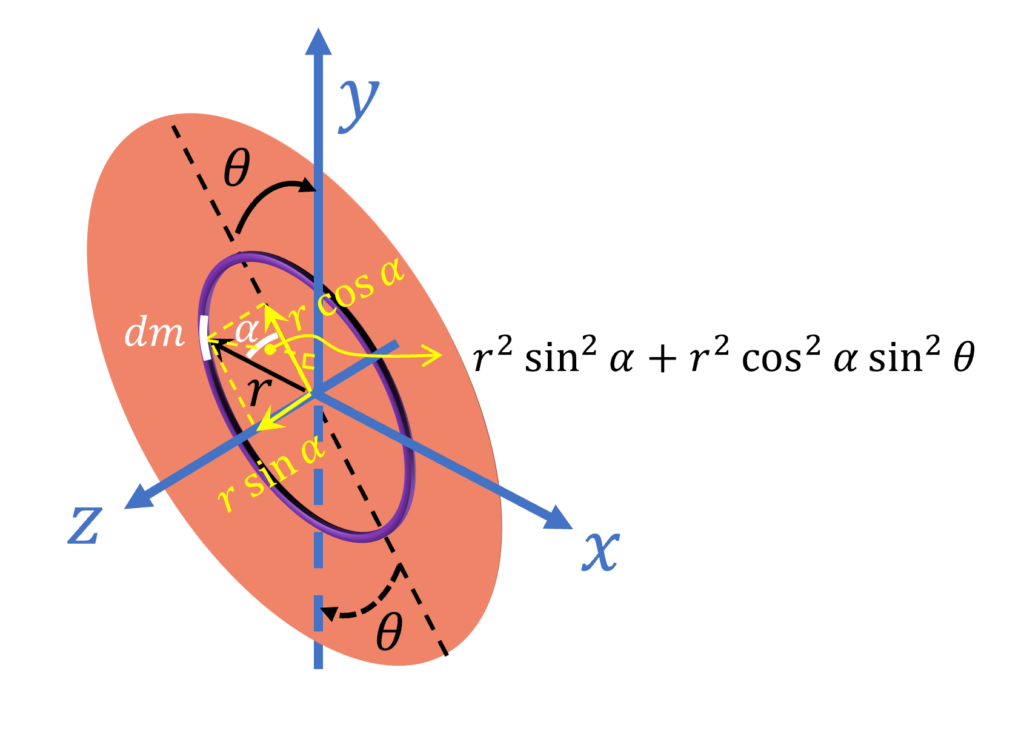
Moment of inertia of a ring, of mass $M$ and radius $R$, about an axis inclined at an angle $\theta$ with it’s plane is
$= \cfrac{M R^2}{2} (1 + \sin^2 \theta)$
Moment of inertia of disc, of mass $M$ and radius $R$, about an axis inclined at an angle $\theta$ with its plane is
$= \cfrac{MR^2}{4} (1 + \sin^2 \theta)$
Ring:
$dm = \cfrac{M}{2 \pi r} r d \alpha$
$dI = dm r^2 (\sin^2 \alpha + \cos^2 \alpha \sin^2 \theta)$
$= \cfrac{M}{2 \pi r} r^3 (\sin^2 \alpha + \cos^2 \alpha \sin^2 \theta)d \alpha $
$I = \int dI$ $= \cfrac{M}{2 \pi} r^2 \int_{\alpha = 0}^{\alpha = 2 \pi}(\sin^2 \alpha + \cos^2 \alpha \sin^2 \theta)d \alpha$
$=\cfrac{Mr^2}{2} (1 + \sin^2 \theta)$
Disc:
$dm = \cfrac{M}{\pi R^2} 2 \pi r dr$
$dI = \cfrac{dm r^2}{2} (1 + \sin^2 \theta)$
$I = \int dI$ $= \cfrac{M}{\pi R^2} 2 \pi \int_0^R \cfrac{r^3}{2} (1 + \sin^2 \theta) dr$
$= \cfrac{MR^2}{4} (1 + \sin^2 \theta)$
Moment of Inertia of Hollow Cylinder | Annular Disc
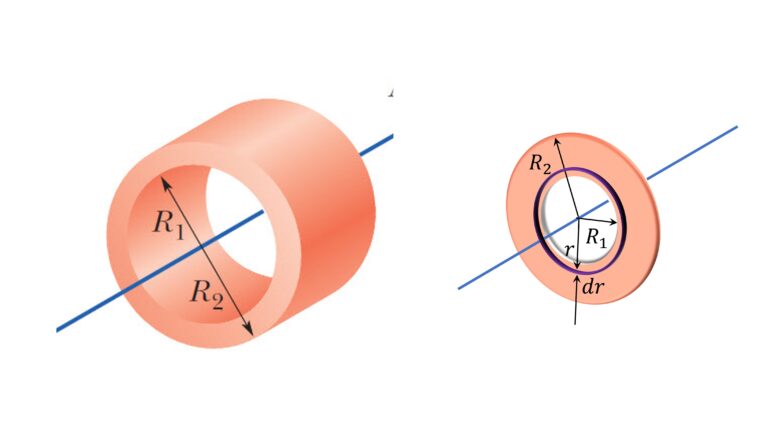
About the central axis:
$I = \cfrac{1}{2} M (R_1^2 + R_2^2)$
About its central axis:
$dI = r^2 dm$
$dm = \cfrac{M}{\pi (R_2^2 – R_1^2)} 2 \pi r dr$
$\implies$ $dI=$ $\int_{r_1}^{r_2} r^2 dm$ $\cfrac{2 M}{R_2^2 – R_1^2} \int_{r_1}^{r_2} r^3 dr$
Or
$I = \cfrac{1}{2} M (R_1^2 + R_2^2)$
Moment of Inertia of Solid Cylinder
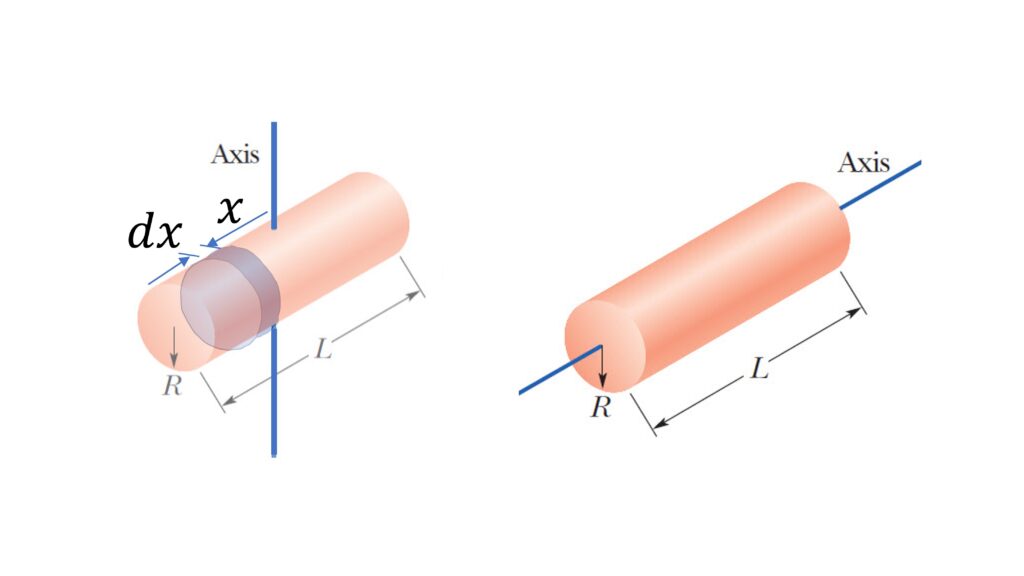
About the axis perpendicular to the length of the rod and passing through its center:
$I = \cfrac{1}{4} MR^2 + \cfrac{1}{12} ML^2$
About the central axis:
$I = \cfrac{1}{2} MR^2$
About the axis perpendicular to its length and passing through its center:
$dI = \cfrac{1}{4} R^2 dm + dm x^2$
$dm = \cfrac{M}{L} dx$
$I = \int dI = \cfrac{1}{4} R^2 \int dm + \cfrac{M}{L} \int_{-L/2}^{L/2} x^2 dx$
$I = \cfrac{1}{4} MR^2 + \cfrac{1}{12} ML^2$
About the central axis:
Same as that of disc about its central axis
Moment of Inertia of a Rod
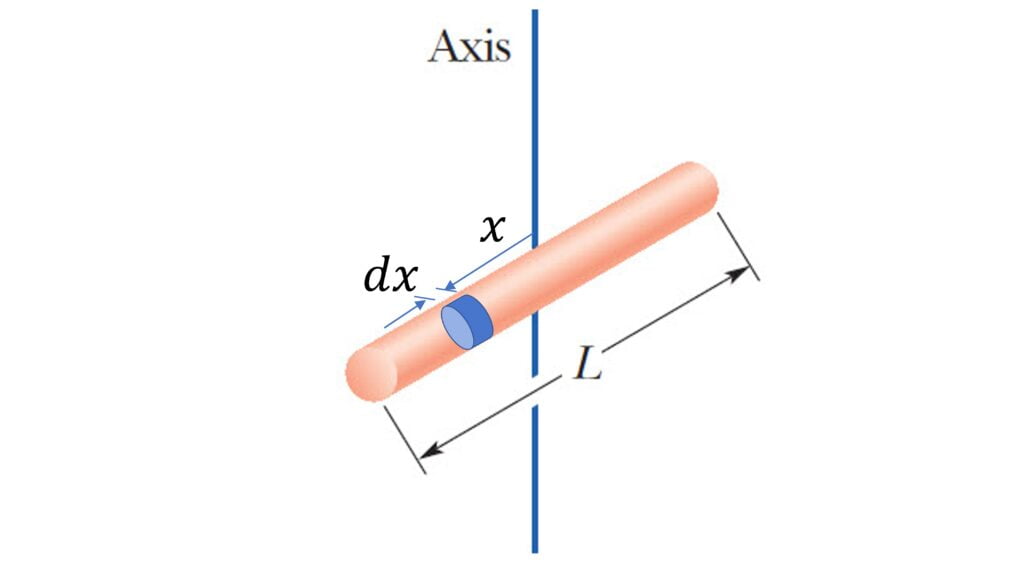
About the axis perpendicular to its length and passing through the center:
$I = \cfrac{1}{12} ML^2$
$dI = \int_{-L/2}^{L/2} x^2 dm$
$dm = \cfrac{M}{L} dx$
$I = \cfrac{1}{12}ML^2$
Moment of Inertia of a Rod About an Inclined Axis
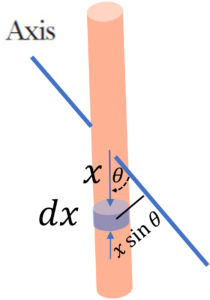
Moment of inertia of rod, of mass $M$ and length $L$, about an axis inclined at an angle $\theta$ with the rod $= \cfrac{ML^2}{12} \sin^2 \theta$
$dm = \cfrac{M}{L} dx$
$dI = dm x^2 \sin^2 \theta$
$I = \int dI =\cfrac{M}{L} \int_{-L/2}^{L/2} x^2 \sin^2 \theta dx$
Moment of Inertia of Hollow Sphere
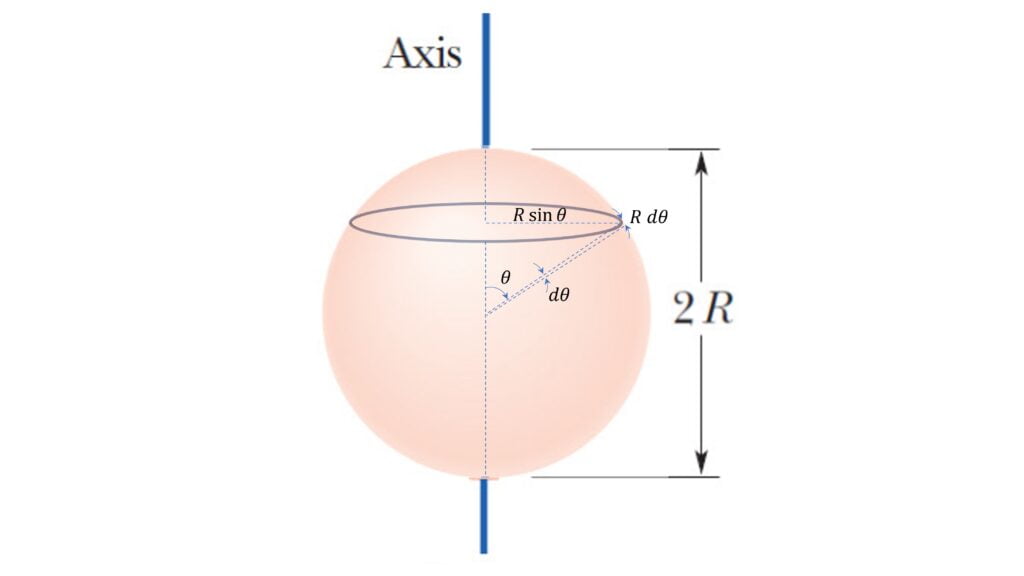
About its diameter:
$I = \cfrac{2}{3} MR^2$
Let’s consider the differential ring of mass $dm$ as shown:
$dm = \cfrac{M}{4 \pi R^2}2\pi R \sin \theta . R d\theta$ $=\cfrac{1}{2} M \sin \theta d \theta$
$dI = R^2 \sin^2 \theta dm$ $=\cfrac{1}{2} MR^2 \sin^3 \theta d\theta$
$I = \int dI$ $= \cfrac{1}{2} MR^2 \int_0^{\pi} \sin^3 \theta d\theta$
$I = \cfrac{2}{3} MR^2$
Moment of Inertia of Solid Sphere
About its diameter:
$I = \cfrac{2}{5} MR^2$
Consider a spherical shell or radius $r$ and thickness $dr$
For this differential strip,
$dm = \cfrac{M}{\cfrac{4}{3} \pi R^3} 4 \pi r^2 dr$ $=\cfrac{3M}{R^3} r^2dr$
$dI = \cfrac{2}{3} dm r^2$ $=\cfrac{2M}{R^3} r^4 dr$
$I = \cfrac{2M}{R^3} \int_0^R r^4 dr$ $=\cfrac{2}{5} MR^2$
Moment of Inertia of Rectangle | Rectangular Plate
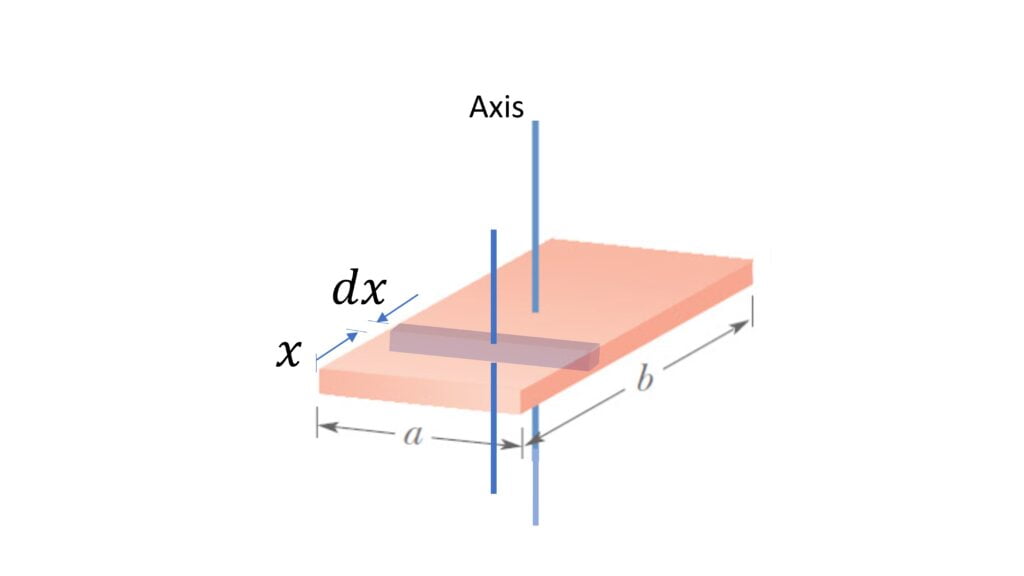
About the axis passing through its center and perpendicular to its plane,
$I = \cfrac{M}{12} (a^2 + b^2)$
Let’s consider differential rod like element of width $dx$,
$dm = \cfrac{M}{ab}adx$ $=\cfrac{M}{b} dx$
$dI = \cfrac{1}{12} dm a^2 + dm (\cfrac{b}{2} – x)^2$
$I = \int dI$ $=\cfrac{1}{12} \cfrac{Ma^2}{b} \int_0^b dx + \cfrac{M}{b} \int_0^b (\cfrac{b^2}{4} + x^2 – bx)dx$
$I = \cfrac{1}{12} M (a^2 + b^2)$
Moment of Inertia of Square Plate
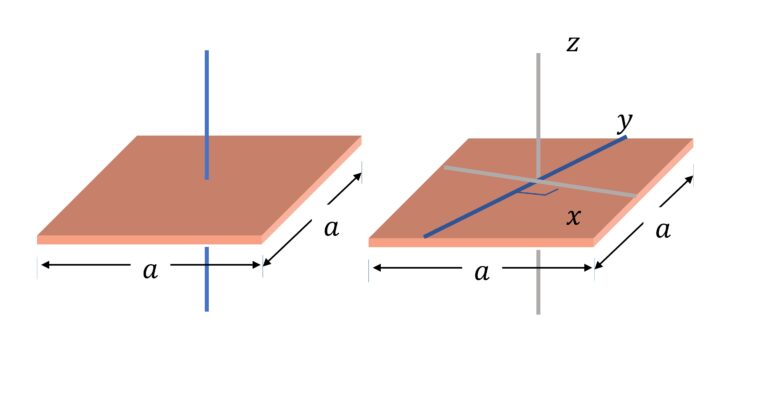
About the axis through its center and perpendicular to its plane:
$I = \cfrac{1}{6} Ma^2$
About the axis passing through its center and in the plane of the square:
$I = \cfrac{1}{12} Ma^2$
About the axis through its center and perpendicular to its plane:
Derivation is same as that for rectangular plate
About the axis passing through its center and in plane of the square ($I_x$ or $I_y$):
From perpendicular axis theorem: $I_z = I_x + I_y$
From Symmetry $I_x = I_y$
$\implies$ $I_x = I_y = \cfrac{1}{12} Ma^2$
Moment of Inertia of Cube
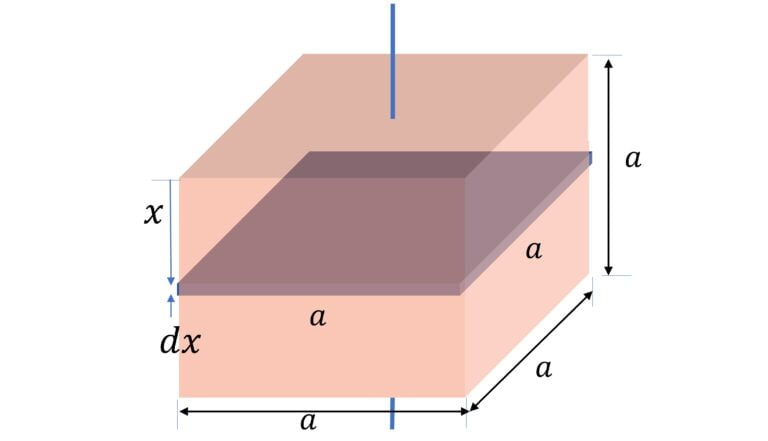
About an axis passing through its center and perpendicular to any two faces,
$I = \cfrac{1}{6} Ma^2$
Consider the differential square plate element of thickness $dx$
$dm = \cfrac{M}{a^3} a^2 dx$ $= \cfrac{M}{a} dx$
$dI = \cfrac{1}{6} a^2 dm$
$I = \int dI = \cfrac{1}{6} Ma \int_0^a dx$
$I = \cfrac{1}{6} Ma^2$
Moment of Inertia of Triangle
1) Moment of Inertia of Equilateral Triangle about centroid
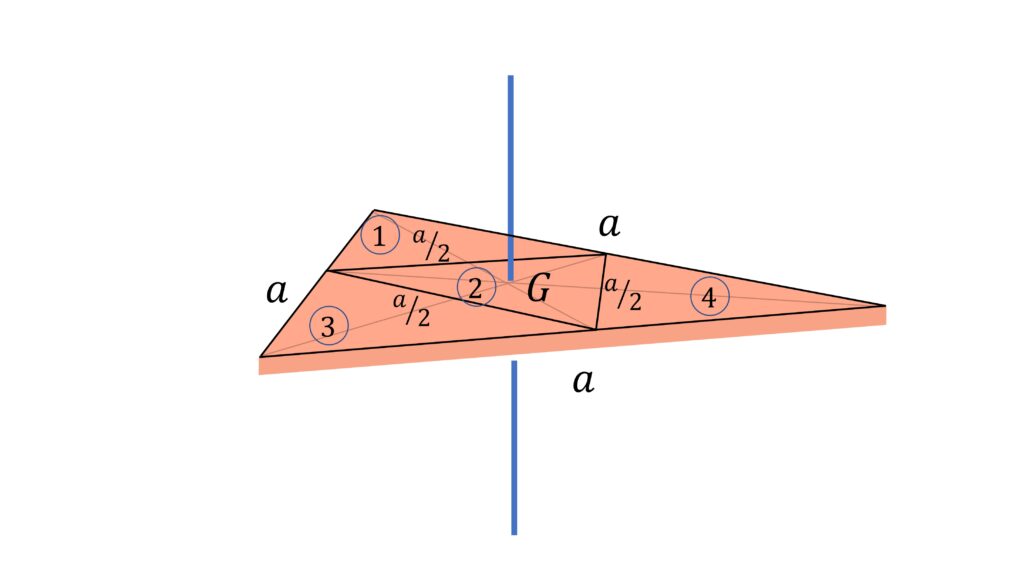
Moment of inertia about an axis passing through the centroid and perpendicular to the triangle, $I = \cfrac{1}{12} Ma^2$
Let’s find the moment of inertia of an equilateral triangle of side $a$ indirectly by dividing the equilateral triangle into 4 equilateral triangles of slide $\cfrac{a}{2}$ as shown.
Now, the moment of inertia is proportional to mass and square of the side lengths,
So moment of inertia of smaller equilateral triangles, $i$, (about perpendicular axis passing through their centroids) would be $\cfrac{1}{16}$ of the moment of inertia $I$ of the full triangle
So using parallel axis theorem, we can write
$I = 4 \times \cfrac{I}{16} + 3 \times \cfrac{M}{4} \times (\cfrac{a}{2 \sqrt{3}})^2$
Or, $I = \cfrac{1}{12} Ma^2$
2) Moment of Inertia of Triangle (of base $a$ and height $h$) about centroid (with axis in-plane of triangle)
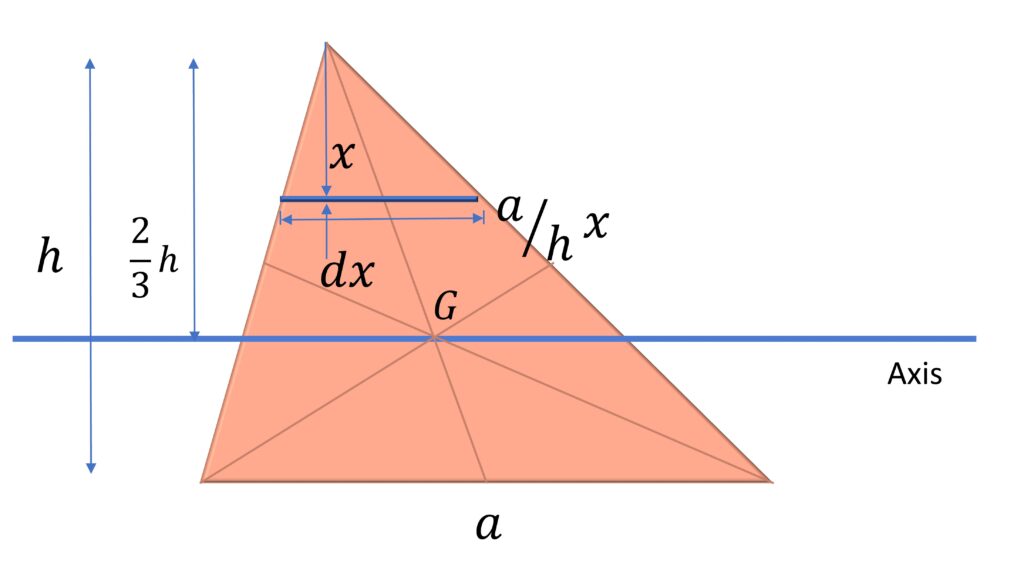
Moment of inertia about the axis passing through centroid and parallel to base:
$I = \cfrac{\rho ah^3}{36} = \cfrac{Mh^2}{18}$
3) Moment of Inertia of Triangle (of base $a$ and height $h$) about its base
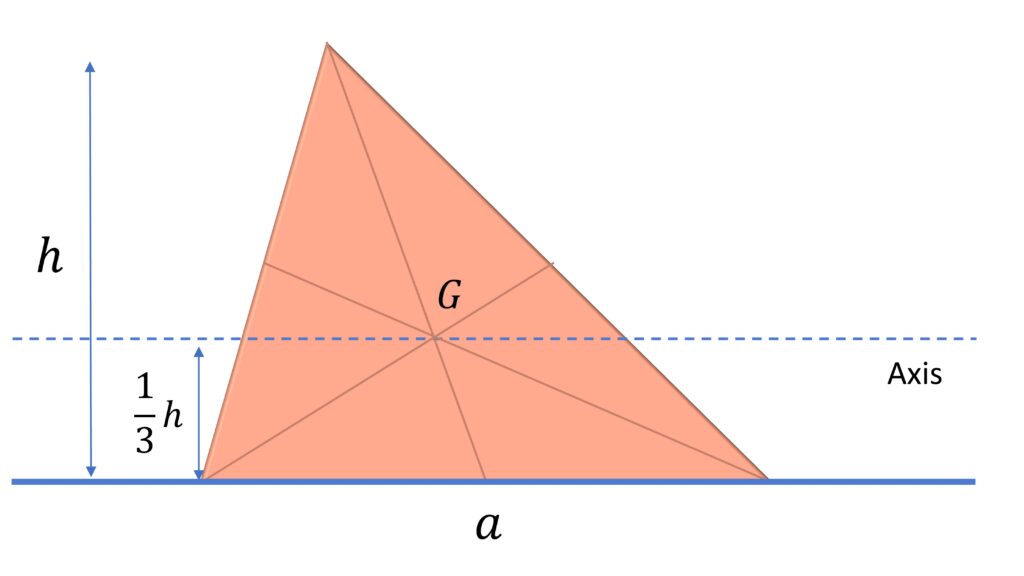
Moment of inertia about the base:
$I = \cfrac{\rho ah^3}{12} = \cfrac{Mh^2}{6}$
Using parallel axis theorem:
$I_{base} = I_{centroid} + M(\cfrac{h}{3})^2$ $=\cfrac{Mh^2}{6}$
Moment of Inertia of Solid Cone
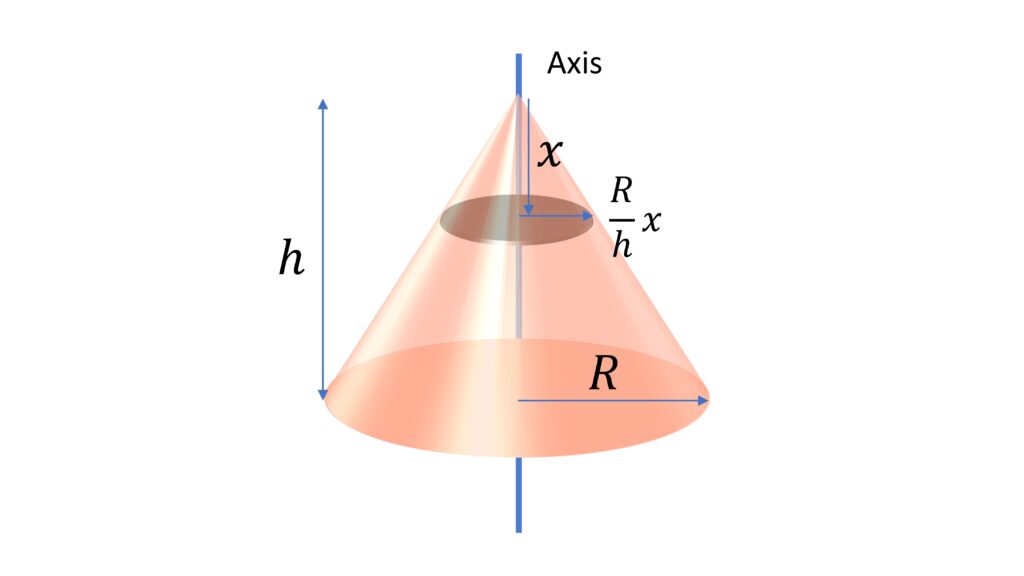
Moment of inertia of solid cone about its central axis, $I$ $=\cfrac{3}{10} MR^2$
Consider the differential disc element as shown
$dm = \cfrac{M}{\cfrac{1}{3} \pi R^2 h} \pi (\cfrac{R}{h} x)^2 dx$
$dI = \cfrac{1}{2} (\cfrac{R}{h} x)^2 dm$
$I = \int_0^h dI$




its very useful sir
Very nicely explained and composed. The derivation part is the best.