Now let’s explore projectile motion on inclined plane, wherein, a projectile is thrown at an angle from the inclined surface. Here we would establish the time of flight and range along the inclined plane.
Time of flight and range of projectile on inclined plane
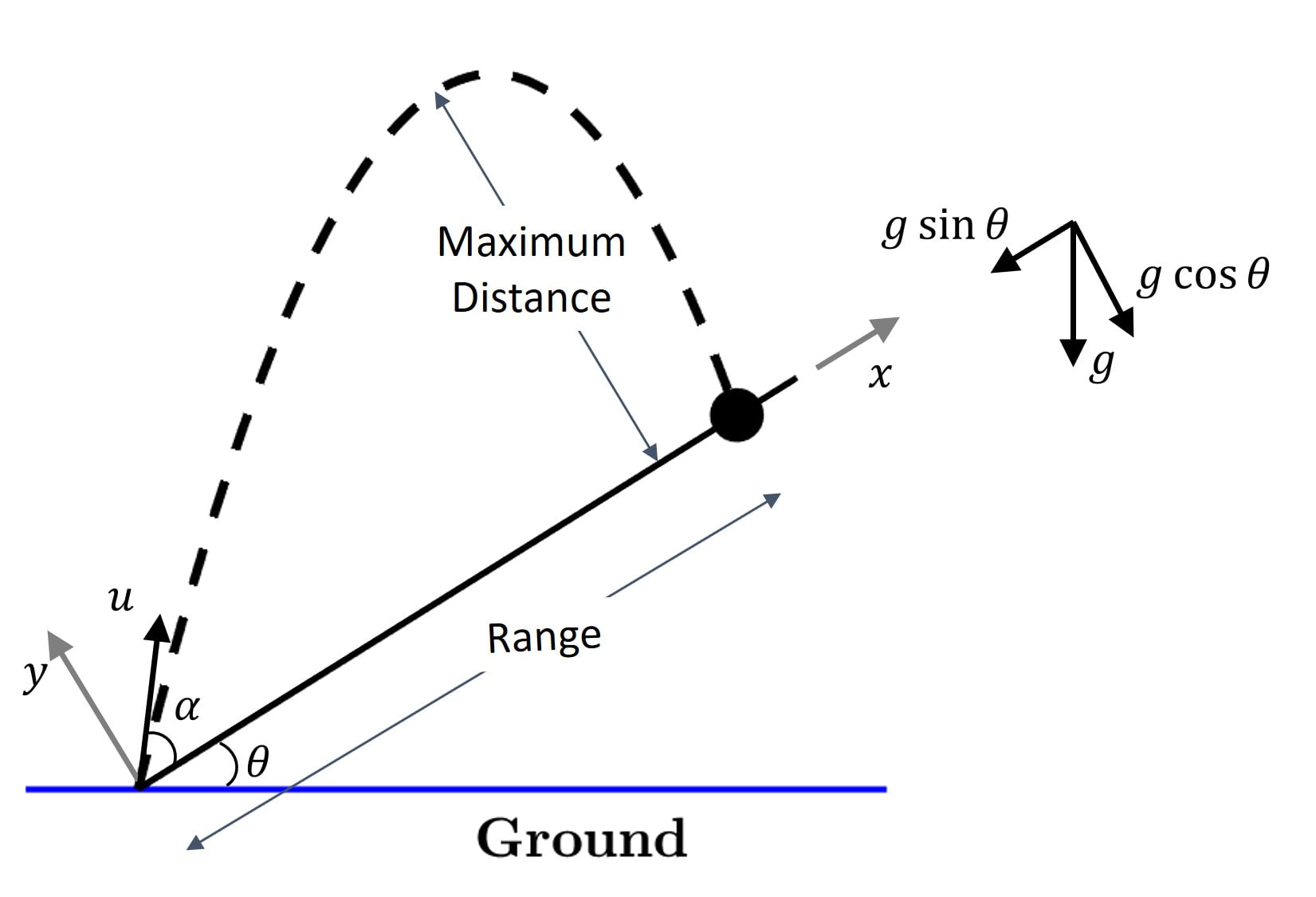
Let’s choose the $x$ axis to be along the inclined plane and $y$ axis to be perpendicular to the inclined plane and pointed away from it.
Now, the acceleration along the $x$ axis is $-g \sin \theta$ and acceleration along $y$ axis is $-g \cos \theta$.
So, let’s begin with time of flight, $T$, i.e. time it takes for the projectile to land back on the inclined plane. Note that net displacement over time duration $T$, along the chosen $y$ axis, is zero i.e. $y =$ $u_y T -$ $\cfrac{1}{2} g \cos \theta T^2 = 0$, where $u_y = u \sin \alpha$, which means $T=\cfrac{2 u \sin \alpha}{g \cos \theta}$
So, how much distance does the projectile travel along the incline during this time period $T$? Well, the displacement or range along the inclined plane would be $x = u_x T -$ $\cfrac{1}{2} g \sin \theta T^2$ $=\cfrac{2 u^2 \sin \alpha \cos (\theta + \alpha)}{g \cos^2 \theta}$
Maximum range of projectile on inclined plane
Range $=\cfrac{2 u^2 \sin \alpha \cos (\theta + \alpha)}{g \cos^2 \theta}$ would be maximum when $\cfrac{dR}{d \alpha} = 0$, or when $\alpha = \cfrac{\pi}{4} – \cfrac{\theta}{2}$
Maximum distance of projectile from the inclined plane
At maximum distance, $H$, $v_y = 0$, so using $v_y^2 = u_y^2 – 2 g \cos \theta H$ or $H = \cfrac{u^2 \sin^2 \alpha}{2 g \cos \theta}$
Projectile Motion | Important Questions | JEE PYQs
- Types of projectile motion
- Equations of projectile motion
- Range of a projectile
- Maximum height of a projectile
- Trajectory of a projectile
- Radius of curvature of projectile
- Velocity of projectile at time $t$ or height $h$
- Projectile Motion Examples
- Projectile motion along an inclined plane
- Relative motion of projectile(s)
Kinematics Overview – What you need to know for JEE Main and JEE Advanced