Here are the 20 pulley problems for IIT JEE and JEE Main that will help you improve on your free body diagrams and your ability to correctly apply newton’s 2nd law $F=ma$.
And yes, do listen through the explanation video by Vikas Sir (IIT Delhi Alumni) towards the end which will help you build a solid foundation and if you have any questions, please leave us a comment at the bottom.
For those, who need ‘Pulley Problems IIT JEE PDF’, you can simply take a print of this page.
Pulley Problems | Motion of masses geometrically connected
Geometrically connected | Masses moving vertically
Q1. Two blocks $’A’$ and $’B’$ having masses $m_A$ and $m_B$, respectively, are connected by an arrangement shown in the figure. Calculate the downward acceleration of the block $B$. Assume the pulleys to be massless. Under what condition will block $A$ have downward acceleration ?
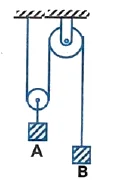
$2g \ (2m_B – m_A)/(4m_B + m_A)$; when $m_A > 2m_B$
Q2. Strings and pulleys are massless and frictionless. The relation between accelerations of the blocks as shown in the figure is
(A) $a_2 = 6a_1$ (B) $a_1 = 6a_2$
(C) $a_1 = 3a_2$ (D) $a_2 = 3a_1$
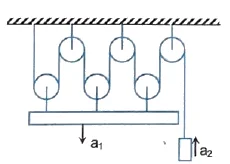
Correct answer is (A).
Q3. Find the acceleration of block mass $m$. Assume pulleys are of massless and frictionless.
(A) $g/3$ (B) $2g/3$
(C) $g/2$ (D) None of these
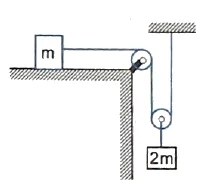
Correct answer is (B)
Q4. Three equal weights of mass $2 \ kg$ each are hanging on a string passing over a fixed pulley as shown in the figure. What is the tension in the string connecting weights $B$ and $C$ ?
(A) zero (B) $13.3 \ N$
(C) $3.3 \ N$ (D) $19.6 \ N$
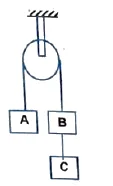
Correct answer is (B).
Let’s say that the tension in string connecting $B$ and $C$ is $T_1$ and that in the string connecting $A$ and $B$ is $T_2$
and let’s say that $B$ and $C$ are moving downwards with an acceleration $a$,
Then writing newton’s 2nd law for $A$, $B$ and $C$ we get the following 3 equations in 3 unknowns ($T_1$, $T_2$ and $a$)
$A$: $T_2 – 2g = 2a$
$B$: $T_1 + 2g – T_2 = 2a$
$C$: $2g – T_1 = 2a$
Solving the 3 equations we will get $T_1 = 13.3$ N.
Geometrically connected | Masses moving horizontally
Q5. Find the relation between acceleration of the blocks in the figure. The pulley and the strings are massless. (where $a = $ acceleration of $m$ and $A = $ is the acceleration of $M$)
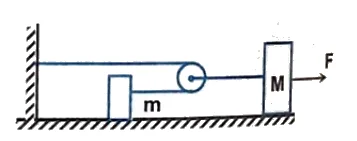
$a = 2A$
Geometrically connected | Some masses moving vertically and some horizontally / along an incline
Q6. Calculate the acceleration of the block $A$ and $B$ in the given diagram.
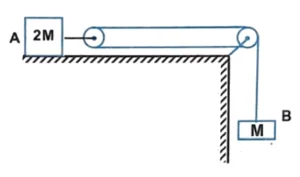
$g/3, \ 2g/3$
Q7. Calculate the acceleration of the block $A$ and $B$ in the given figure.
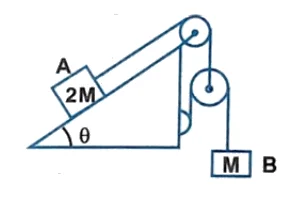
$\cfrac{g(1 – \sin \theta)}{3}, \ \cfrac{2g(1 – \sin \theta)}{3}$
Q8. If the blocks $A$ and $B$ are moving towards each other with acceleration $a$ and $b$ as shown in the figure. Find the net acceleration of block $C$.
(A) $a \hat{i} – 2(a + b) \hat{j}$ (B) $- (a + b) \hat{j}$
(C) $a \hat{i} – (a + b) \hat{j}$ (D) None of these
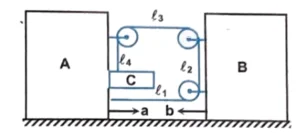
Correct answer is (A).
Q9. In the figure shown, what will be the acceleration of the block $B$ if that of the $A$ is $0.3 \ m/s^2$
(A) $0.15 \ m/s^2$ (B) $0.6 \ m/s^2$
(C) $0.3 \ m/s^2$ (D) None of these
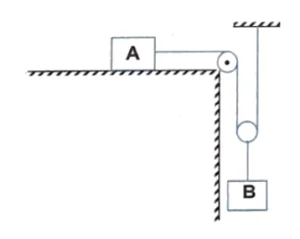
Correct answer is (A).
Q10. The frictional co-efficient between the board and the floor shown in figure is $\mu$. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor. The mass of man is $M$ and the mass of plank is $m$.
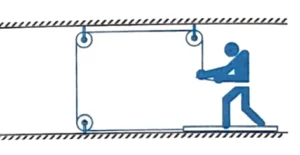
$\cfrac{\mu(m + M)g}{(1 + \mu)}$
Q11. Two bodies of masses $5 \ kg$ and $4 \ kg$ are arranged in two positions as shown in the figure. (A) and (B), if the pulleys and the table are perfectly smooth, the acceleration of the body in case (A) and (B) are:
(A) $g$ and $(5/9) \ g$ (B) $(4/9) \ g$ and $(1/9) \ g$
(C) $(g/5)$ and $(g/5)$ (D) $(5/9) \ g$ and $(1/9) \ g$
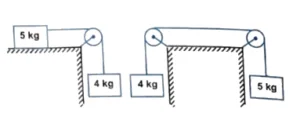
Correct answer is (B).
Geometrically connected | Complex motion
Q12. A block $A$ constrained to slide along the incline plane of the wedge $B$. Block $A$ is attached with a string which passes through three ideal pulleys and connected to the wedge $B$. If the wedge is pulled towards right with an acceleration $’a’$.
(a) Find the acceleration of the block with respect to wedge.
(b) Find the acceleration of the block with respect to ground.
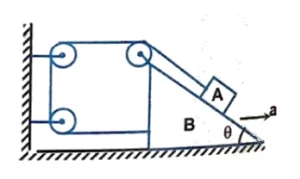
(a) $2a$, (b) $a\sqrt{5 – 4 \cos \theta}$
Pulley Problems | Independent motion of masses
Independent Motion | Masses moving vertically
Q13. In the system shown in the figure, a bead of mass $m$ can slide on the string. There is friction between the bead and the string. Block $B$ has mass equal to twice that of the bead. The system is released from rest with length $l = 18.75 \ m$ of the string hanging below the bead. Assuming the pulley and string to be massless. Find the distance (in meter) moved by the block $B$ before the bead slips out of the thread.
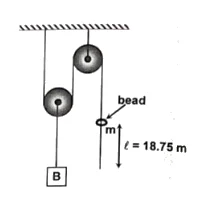
$6.25$
Independent Motion | Some masses moving vertically and some horizontally
Q14. Three blocks of mass $m_1, \ m_2$ and $m_3$ are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of $m_1$.
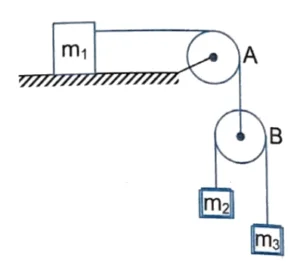
$\cfrac{g}{1 + \cfrac{m_1}{4}\left(\cfrac{1}{m_2} + \cfrac{1}{m_3}\right)}$
Q15. Consider the situation shown in the figure. The horizontal surface below the bigger block is smooth. The coefficient of friction between the blocks is $\mu$. Find the minimum and the maximum force $F$ that can be applied in order to keep the. smaller blocks at rest with respect to the bigger block.
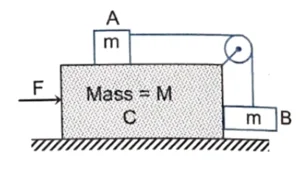
$F_{\text{min}} = \cfrac{1 – \mu}{1 + \mu}(M + 2m)g$, $F_{\text{max}} = \cfrac{1 + \mu}{1 – \mu}(M + 2m)g$
Q16. A truck shown in the figure is driven with an acceleration $a = 3 \ m/s^2$. Find the acceleration of the bodies $A$ and $B$ of masses $10 \ kg$ and $5 \ kg$ respectively, assuming pulleys are massless and friction is absent everywhere.
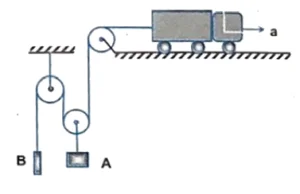
$a_A = a_B = 1 \ m/s^2$ upwards
Q17. A block of mass $2M$ is attached to a massless spring with spring-constant $k$. This block is connected to two other blocks of masses $M$ and $2M$ using two massless pulleys and strings. The accelerations of the blocks are $a_1, \ a_2$ and $a_3$ as shown in the figure. The system is released from rest with the spring in its un stretched state. The maximum extension of the spring is $x_0$. Which of the following option(s) is/are correct ? [$g$ is the acceleration due to gravity. Neglect friction]
(A) At an extension of $\cfrac{x_0}{4}$ of the spring, the magnitude of acceleration of the block connected to the spring is $\cfrac{3g}{10}$
(B) $x_0 = \cfrac{4Mg}{k}$
(C) When spring achieves an extension of $\cfrac{x_0}{2}$ for the first time, the speed of the block connected to the spring is $3g\sqrt{\cfrac{M}{5k}}$
(D) $a_2 – a_1 = a_1 – a_3$
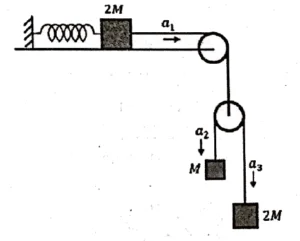
According to constraint relation
$a_1 = \cfrac{a_2 + a_3}{2} \Rightarrow a_1 – a_3 = a_2 – a_1$
$\Rightarrow $ Option (d) is correct.
Let “x” be the extension of the spring at a certain instant. Then
$2T – k_x = 2Ma_1$
$2Mg – T = 2Ma_3$
$Mg – T = Ma_2$
On solving we get,
$a_1 = \cfrac{4g}{7} – \cfrac{2kx}{14M}$ …(i)
$\therefore \omega ^2 = \cfrac{3k}{14M} \quad \omega = \sqrt{\cfrac{3k}{14M}}$
and $T = \cfrac{4Mg}{7} + \cfrac{2kx}{7}$ …(ii)
For $a_1 = 0$ (maximum extension of spring) we have from (i)
$\cfrac{4g}{7} – \cfrac{3kx}{14M} = 0$
$\therefore 4g = \cfrac{3kx}{2M} \qquad \therefore x = \cfrac{8Mg}{3k}$
$\therefore x_0 = 2x = \cfrac{16Mg}{3k}$
For $x = \cfrac{x_0 }{4} = \cfrac{1}{4} \left( \cfrac{16Mg}{3k} \right) = \cfrac{4Mg}{3k}$
From (i) $a_1 = \cfrac{4g}{7} – \cfrac{3k}{14M} \times \cfrac{4Mg}{3x} = \cfrac{2g}{7}$
At $x = \cfrac{x_0}{2} $ the particle is at the mean position and its velocity = $A \omega$
$ = \cfrac{x_0}{2} \sqrt{\cfrac{3k}{14M}} = \cfrac{8Mg}{3k}\sqrt{\cfrac{3k}{14M}}$
Pulley Problems | External force acting on rope / pulley
Q18. The acceleration of the $2 \ kg$ block if the free end of string is pulled with a force of $20 \ N$ as shown is
(A) $0$ (B) $10 \ m/s^2$
(C) $5 \ m/s^2$ upward (D) $5 \ m/s^2$ downward
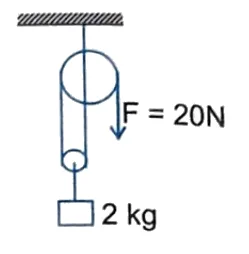
Correct answer is (B).
Q19. Two blocks of mass $m = 5 \ kg$ and $M = 10 \ kg$ are connected by a string passing over a pulley $B$ as shown. Another string connects the center of pulley $B$ to the floor and passes over another pulley $A$ as shown. An upward force $F$ is applied at the center of pulley $A$. Both the pulleys are massless. Find the acceleration of blocks $m$ and $M$ if $F$ is :
(a) $100 \ N$
(b) $300 \ N$
(c) $500 \ N$ (take $g = 10 \ m/s^2$)
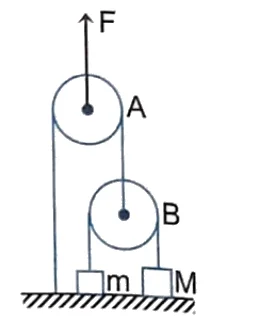
(a) $0, \ 0$
(b) $5 \ m/s^2, \ 0$
(c) $15 \ m/s^2, \ 2.5 \ m/s^2$
Q20. In the arrangement shown in figure $m_A = m$ and $m_B = 2m$, while all the pulleys and string are massless & frictionless. At $t = 0$, a force $F = 10 \ t$ starts acting over central pulley in vertically upward direction. Find
(a) Time at which both the masses lose contact with floor.
(b) Velocity of $A$ when $B$ loses contact with floor.
[Take all the units into S.I. system, take $m = 1 \ kg$ and $g = 10 \ m/s^2 for part (b)]
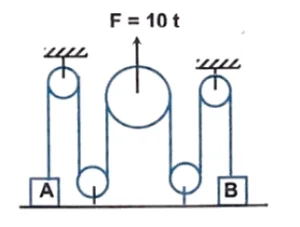
(a) $\cfrac{2mg}{5} \ s$
(b) $10 \ m/s$
Explanation Video by Vikas Sir
Covers question no’s 1, 2, 3, 4, 13, 16, 18, 19, 20




